2025年1月20日、中国のAI開発スタートアップDeepSeek社が、新たな推論モデル 「DeepSeek-R1」 を発表した。このモデルは、現時点での最高性能を誇るOpenAI社のChatGPT-o1モデルに匹敵、あるいは凌駕するとも言われる高い性能を示し、全世界で爆発的に普及した。
性能もさることながら、真に驚くべきはその開発コストの低さである。DeepSeek-R1の開発費用は、ChatGPT-o1のわずか1/10以下とされ、これまでAI開発に不可欠とされてきた巨額の投資が必ずしも必要でないことを示唆している。特に注目されるのは、米国による中国向けGPUの輸出規制のためにDeepSeekが NVIDIAの型落ちGPU「H800」 を使用してモデルの構築に成功した（と言われている）点である。これは、莫大なコストをかけて最先端のGPU、H100やB200を大量投入する米国のAI開発とは対照的である。一部では「GPUの輸出規制」というハンデが却って中国企業の技術向上を促進してしまった、という意見も見られる。
DeepSeek-R1は単にハードウェアの最適化によってコストを削減しただけではなく、モデルの学習方法やアーキテクチャのブレイクスルーにより、技術的にも革新的な手法が取り入れられている。このため、コスト面の優位性に加え、学術的な関心をも引きつけているという側面がある。
これらの優位性によってDeepSeek社は価格破壊レベルの安さでAPIを提供しており、米国のAI事業者の競争力低下が危惧される事態になった。実際、このニュースを受けてNVIDIAの株価は17％程度下落し、約90兆円（トヨタ自動車の時価総額のおよそ2倍）が失われたことが話題になった。またAIの学習に大量のGPUが必要でない可能性が開けたことで、電力消費の増大を見込んでいた電力インフラ関連株も大きく売られた。
しかし現在、DeepSeekがOpenAIの規約に違反して「ChatGPTの出力結果を教師データとしてDeepSeek-R1モデルの訓練に利用している」との報道があり、OpenAIとMicrosoftが調査に乗り出す意向を示している。不正なデータ利用の可能性を受け、米海軍ではセキュリティと倫理的な懸念から業務でのDeepSeekの使用禁止を通達。イタリアではDeepSeekのダウンロードが禁止されるなど、データの安全性が疑問視されるDeepSeekの利用制限に踏み切る動きも出てきている。
今、生成AI開発の舞台で何が起こっているのか、少し整理してみたい。
※お断り：本稿の内容の大半は2025年1月末頃に執筆されたものです。最新の情報を参照するように努めていますが、4月現在では状況が少し変わっている可能性があります。記事の内容そのものは一般論的なものになっていますが、上記の点についてお含みおきください。
OpenAI-o1モデルの概略
ご存知の通り、2022年11月にOpenAI社がChatGPTを公開して以降、生成AI（Generative Artificial Intelligence）は世界中で爆発的に普及した。文章生成を始めとして日常的なタスクからビジネスシーンでのアイデア出し、文献調査や科学的な推論など、様々な作業をこなすことができる。読者の中にも利用したことのある方は多いだろう。
OpenAI社はこれまでにいくつかのGPTモデルを発表しており、2025年2月現在最もよく使われているのがGPT-4oのモデルである。2024年9月にはGPT-4oの高精度版モデルであるOpenAI-o1のプレヴュー版が公開され、12月にはo1のフルモデル及びo1 pro modeを公開。理数系分野の解析・推論など、複雑な思考を要するタスクに対応できるようになった。
これらのモデルは有料版プランでしか提供されていないが、今後のアップデートで無料ユーザーにも順次公開していくとのことである。
DeepSeekの話題にもつながるので、ここで少し詳しくChatGPTのo1モデルについて整理しておこう。
OpenAI-o1では「Chain of Thought（思考連鎖）」と呼ばれる推論手法が利用されている。これは回答を生成する前に「考える」時間を設け、内部で思考プロセスを段階的に展開し、問題を細分化するという手順を踏む手法である。実際、o1にタスクを与えると、出力に要する時間とは別に数分～十数分程度の待ち時間が発生する。この段階で、o1はタスクに対する回答の論理的正当性を検証している。
例えば、難関大の入試数学などは（解答の根拠が不十分な場合はあるものの）概ね正答を導けるようである。下図に昨年度の東京大学の確率の問題をo1に解かせた例を示したが、12分余りの思考の後、実際にこの問題の正答を与えていることが分かる。
図．o1が東大入試数学に解答する様子（抜粋）
因みに、この時の思考過程はテキストで、しかもリアルタイムで閲覧することができる。長いテキストなので閲覧する際は注意されたい。
» 【o1 proの思考過程はこちら】
（管理人注：数式はKaTeXでレンダリングされることがあるが、ここではテキストとしてコピペしているだけなので無意味な改行が含まれてしまっていることを予めお断りしておく）
Determining the probability p_n is the next step. I’m thinking through how the quadrilateral must include the center O, which is challenging due to symmetry and geometric patterns.
I’m working through a new idea: O is inside the quadrilateral if the vertices don’t form non-sequential arcs greater than 180 degrees.
Calculating the probability involves determining combinations where O remains inside the quadrilateral, considering that no central angle between consecutive vertices should be 180 degrees or more.
OK, let me see. For n=5, seeing that angles are 72 degrees, skipping 3 edges makes a 216-degree arc, which exceeds 180 degrees, leaving O outside the quadrilateral.
I’m thinking about how to ensure O is inside the quadrilateral by avoiding 3 consecutive unchosen vertices, which would place O outside by forming an arc greater than 180 degrees.
You’re piecing together the requirement to avoid arcs of 180 degrees by ensuring each arc between chosen vertices is at most half of (n-1).
To count valid vertex selections where O is inside, I’m figuring out the number of solutions to x1 + x2 + x3 + x4 = n with x_i ≤ (n-1)/2, then dividing by C(n,4).
Now I’m figuring out the count of solutions for y1 + y2 + y3 + y4 = 2k-3, with each y_i ≤ k-1, and subtracting invalid solutions to ensure the constraints are met.
I’m using the principle of inclusion-exclusion to count valid vertex selections for O to be inside the quadrilateral, ensuring no constraints are violated in the counting process.
I’m piecing together the inclusion-exclusion principle to count valid solutions, ensuring constraints aren’t violated. Each solution corresponds to a distinct choice of vertices, considering any starting point.
I’m thinking about potential overcounting when considering any starting vertex as ‘a’. The symmetry of the polygon might lead to duplicate counts of the same set of 4 vertices.
To avoid overcounting, it’s essential to ensure each circular distance between consecutive vertices is less than n/2. This prevents identical sets from being counted more than once.
OK, let me see. By ensuring the smallest chosen vertex is unique and within 1 to n, we effectively avoid overcounting and confirm each set remains distinct.
Taking a closer look at distinct sets of 4 vertices, each solution in A has n variations by positioning the first vertex differently, ensuring no overcounting or rotational symmetry.
Hmm, that’s interesting. It seems odd n prevents rotational symmetry for four evenly spaced vertices, ensuring no overcounting of sets. The total count is n times solutions in A.
To determine
p
n
p
n
, I’ll calculate the number of valid solutions
#
# in
A
A, subtracting overcounted sets, and divide by
C
(
n
,
4
)
C(n,4).
I’ve simplified the expression for valid solutions and derived a general formula for counting the number of solutions in
A
A. Now, it’s time to iterate and finalize specific values.
Let’s expand and simplify the valid sets for
n
=
2
k
+
1
n=2k+1. The final formula will be a ratio of expanded terms to
C
(
n
,
4
)
C(n,4).
I’ve expanded and simplified the product of terms involving
k
k and
n
n to derive the number of valid sets, ensuring the formula accurately reflects the constraints and symmetry of the problem.
I’m simplifying the denominator of the formula by factoring and dividing by 24, ultimately reducing the expression to a more manageable form as [4k^4 -4k^3 – k^2 + k]/6.
OK, let’s simplify the fraction by factoring both the numerator and denominator. This helps streamline the expression for better clarity and easier calculation.
I’m working through the numerator and denominator to identify common factors and simplify. Unfortunately, the terms don’t factor nicely, so the expression remains complex. Progressing, though a bit tricky!
I’m digging into the numerator to identify if it can be simplified with factors like
k
(
k
−
1
)
(
4
k
2
−
1
)
k(k−1)(4k
2
−1), aiming for a more concise rational function form. This approach feels methodical.
OK, let’s break down the polynomial division and factor the numerator. This leads to finding the remainder and simplifying the expression for clearer insights into the polynomial relationship.
Evaluating the remainder, it seems the polynomial simplification might be incorrect. The probability p_n should be less than 1, which suggests a reevaluation of the arcs and constraints is necessary.
OK, let’s think this through: O is outside if all 4 vertices fit within a 180-degree arc. This guidance refines the probability calculation for O to be inside the quadrilateral.
I’m mapping out the number of ways to choose 4 vertices within half the total vertices, ensuring compliance with the 180-degree arc constraint and refining the calculation for O inside the quadrilateral.
To determine p_n, we need to calculate the probability that all four vertices lie within a semicircle, ensuring the center is outside the quadrilateral.
I’m calculating how many ways four distinct vertices can fit within a semicircle, mindful that for odd n, a semicircle contains exactly (n+1)/2 vertices. Progress is steady and methodical.
I’m concluding that for n=5, the probability p_5=1, as removing one vertex from the n-gon ensures the remaining quadrilateral includes the center O. Progress towards a clear solution!
For n=7, each semicircle holds 4 vertices. Assessing distinct semicircles, I find 7 unique ones, with each semicircle hosting either 4 or 3 vertices, depending on their arrangement.
Calculating the number of ways to pick 4 vertices within a semicircle of an n-gon, I see that this involves combinations of consecutive vertices and their circular configurations.
I’m making sure to account for overlaps when a set of 4 vertices might fit within two semicircles. Each set should uniquely match one semicircle, avoiding double-counting.
I’ve nailed down that any set of 4 vertices fitting in a semicircle aligns uniquely with one semicircle, completely avoiding overlaps. This clarifies the counting process for p_n.
I’m mapping out if 4 vertices can fit within a semicircle, ensuring each set matches exactly one semicircle to avoid counting overlaps. This leads me to validate the unique fit condition.
OK, let’s validate: the formula for selecting 4 vertices in a semicircle is
n
×
(
(
n
−
1
)
/
2
3
)
n×(
3
(n−1)/2
). Confirming this matches the number of sets of 4 vertices.
OK, let me see: we select the semicircle’s start in
n
n ways and the remaining 3 vertices from
(
n
−
1
)
/
2
(n−1)/2, forming 4 vertices. This approach ensures a practical solution.
I’ve confirmed the formula for p_n by checking specific values, ensuring the probability of all 4 vertices lying within a semicircle matches the expected result.
I’m honing the formula for p_n by selecting the semicircle’s start in
n
n ways and the remaining 3 vertices from
(
n
−
1
)
/
2
(n−1)/2, ensuring clarity in the probability calculation.
I’m thinking through the probability formula for p_n by assessing the number of ways to choose 4 vertices from a semicircle with
n
n vertices, ensuring the result aligns with known outcomes for odd
n
n.
Choosing the “start” for the semicircle could lead to overcounting since each block of consecutive vertices is distinct. I’m thinking through ways to handle this to accurately determine the probability.
I’m focusing on calculating the distinct ways to select 4 vertices within a block of
(
n
+
1
)
/
2
(n+1)/2. Ensuring no overcounting involves considering the block’s leftmost vertex. This perspective shot offers a strategic approach.
I’m thinking about counting the number of 4-element subsets contained entirely within a block of
(
n
+
1
)
/
2
(n+1)/2 vertices, ensuring no overcounting due to overlapping blocks.
I’m looking at the possibility of overcounting subsets that fit into overlapping blocks. Considering approaches like using distinct blocks and ensuring the maximum arc distance to avoid overcounting.
I’m evaluating the overcounting of subsets in overlapping blocks and considering the number of ways to choose 4 vertices within
(
n
+
1
)
/
2
(n+1)/2 consecutive vertices around the circle to avoid redundancy.
I’m working through the formula for choosing 4 vertices within
(
n
+
1
)
/
2
(n+1)/2 consecutive vertices in an
n
n-gon, ensuring no overcounting due to overlapping blocks. This method guarantees accuracy.
OK, let’s map out that choosing 4 vertices within
(
n
+
1
)
/
2
(n+1)/2 consecutive vertices in an
n
n-gon ensures no overcounting due to overlapping blocks. This method guarantees accurate results.
OK, let me see. I’m exploring how choosing 4 vertices within
(
n
+
1
)
/
2
(n+1)/2 consecutive vertices in an
n
n-gon avoids overlapping blocks, ensuring accurate p_n calculation.
OK, let me see: I’m piecing together a combinatorial approach to ensure no overcounting when selecting 4 vertices within
(
n
+
1
)
/
2
(n+1)/2 consecutive vertices, aiming for a precise calculation of p_n.
I’m evaluating the possibility of overcounting subsets when selecting 4 vertices within
(
n
+
1
)
/
2
(n+1)/2 consecutive vertices, especially when some vertices might be placed in slightly different arcs.
I’m exploring the number of 4-subsets contained in a semicircle and ensuring accuracy by comparing the results for specific
n
n values, leading to the final expression for p_n.
OK, let me see. I’m verifying the final formula for p_n by comparing specific
n
n values and simplifying binomial coefficients, ensuring it aligns with known results for odd and even
n
n.
Piecing together the simplified expression for p_n, I’ve determined that calculating
n
−
5
2
(
n
−
2
)
2(n−2)
n−5
accurately reflects the ratio of binomial coefficients, leading to the final formula for p_n.
» 【思考過程を閉じる】
この例のように、OpenAI-o1は過去のモデルでは実現しなかったような高度な理数系の推論タスクを高い精度でこなしている。推論にある程度時間を要するものの、高校数学などの範囲では中～高レベルの家庭教師として利用するには十分なレベルに達していると言える。
これまで生成AI（特に大規模言語モデル）は、文章生成は得意だが理数系タスクは苦手、という明確な共通認識があった。その点でo1は、従来のモデルとは一線を画す。実際、OpenAI社が公開しているベンチマークテストによれば、数学・物理・化学といった分野でGPT-4oを軒並み大きく上回るスコアをマークしている。
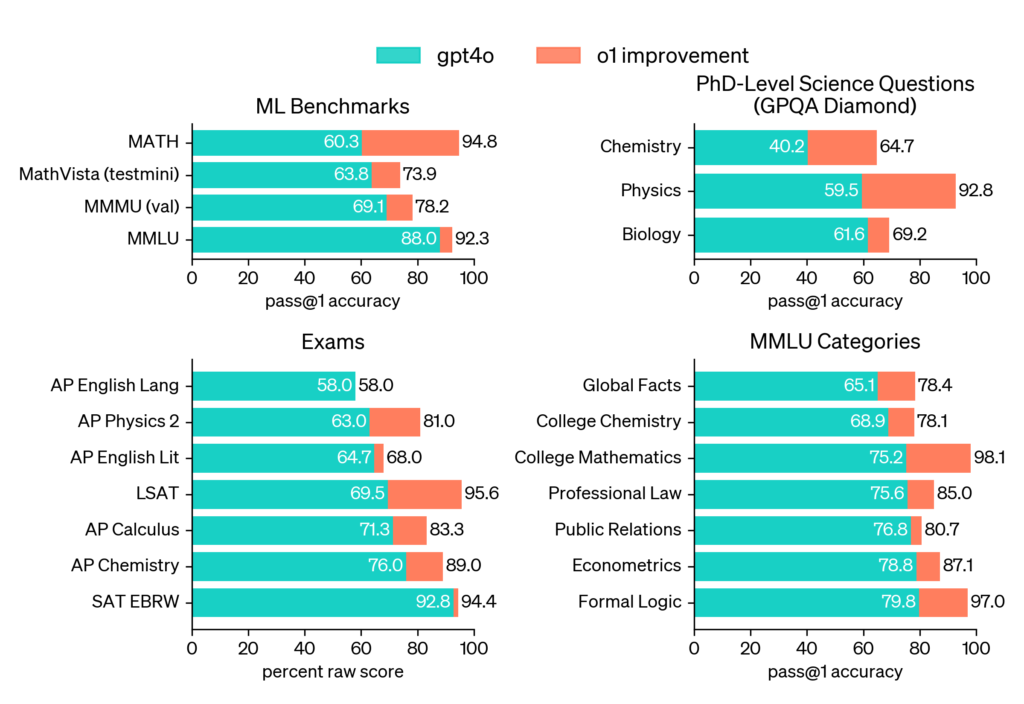
図．各教科のベンチマークテスト
また、数学コンテストや競技プログラミングなどでも人間顔負けの高いスコアを叩き出している。OpenAI-o1の登場を受けて、一部ではAIのレベルを正当に評価できるベンチマークテストが枯渇しかけているとまで言われる状況になっている。こうした評価は、それだけOpenAI-o1が画期的なモデルであったということを意味する。
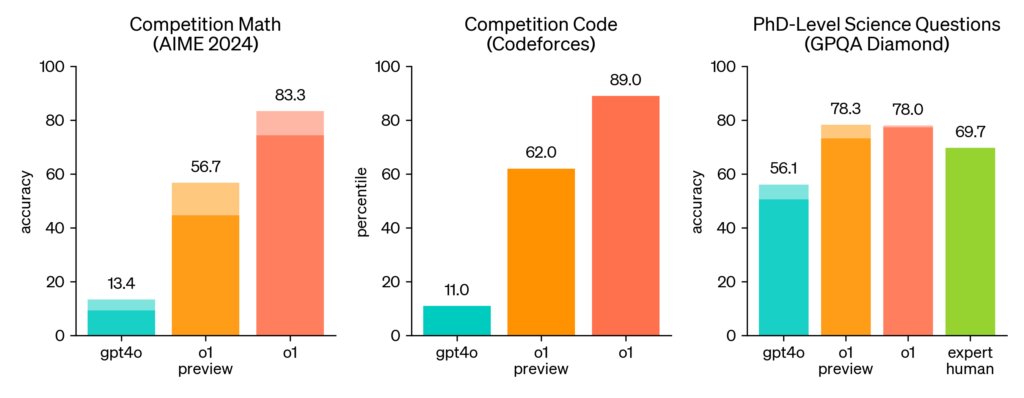図．競技数学などのスコア
せっかくなので少し解説しておこう。このベンチマークに使われているAIME（American Invitational Mathematics Examination）はアメリカで毎年3月頃に2日間かけて開催されている国内向けの数学コンテストの一つである。各問の答えは3ケタの整数と決まっていて、穴埋め形式で回答するという特徴がある。代数、幾何、数論、組み合わせ数学に関連する分野から両日とも15問、計30問が出題され、アメリカの数学オリンピックの代表選抜試験としての役割を有している高難度の試験である。
例として昨年のAIME2024で出題された問題の一つを掲載しておく。全ての問題がここまで難しい訳ではないが、このような難問も含まれているという意味で参考にしていただければと思う。（因みに、管理人が確認したところOpenAI-o1モデルはこの問題に正解できないようである）
Let $p$ be the least prime number for which there exists a positive integer $n$ such that $n^{4}+1$ is divisible by $p^{2}$. Find the least positive integer $m$ such that $m^{4}+1$ is divisible by $p^{2}$.
（和訳）$p$を、次の条件を満たす最小の素数とする：
「ある正の整数$n$が存在して、$n^{4} + 1$ が$p^{2}$で割り切れる。」
このとき、$m^{4} + 1$ が$p^{2}$で割り切れるような最小の正の整数$m$を求めよ。
o1モデルがAIMEにおいて8割以上のスコアをマークしたという事実は実際に驚異的で、数学のかなり得意なアメリカの高校生の中でも上位の成績を獲った、と言えば分かりやすいだろうか。個人的な感度として、年度によっては東大受験生の平均点程度であれば叩き出せると思われる。このような高度な推論能力を実現する方策が思考連鎖なのである。
昔、国立情報学研究所（NII）が人工知能技術のベンチマークの一環として「東ロボくん」というプロジェクトを走らせていた。当時のマーク試験の成績は受験生の平均（※東大受験者ではなく受験生全体での平均）を上回っていたものの、東大の足切りの目安は超えられそうになく、2016年度の時点で合格不能と判断されプロジェクト打ち切りという結果に終わった（計画では2021年までに東大合格を目指していた）。東ロボくんは文系科目の得点が低かったが、現代のLLM技術を以てすれば文系科目の合格ラインはクリアできると思われる。むしろ数理的推論能力では当時最先端を走っていたモデルと言えるだろう。
現在OpenAI社はo3という新しいモデルを開発中で、2025年Q1内にはリリースされるとの見込みである。このo3はo1を大きく上回る推論能力を有するとみられており、AGI（汎用人工知能）の達成に向けたマイルストーンになると言われている。AIによる数理的推論能力が飛躍的に進歩する様を目の当たりにできることが今から楽しみでならない。（参考：OpenAI o3 and o3-mini—12 Days of OpenAI: Day 12）
ところで、OpenAIは、ユーザーがo1の思考連鎖の仕組みを明らかする試みを禁じているようである。利用規約には、思考連鎖の機構を調べる行為を明確に禁止する具体的な記述は見当たらないが、自社が莫大なリソースを費やして構築したモデルを保護するのは当然と言えるだろう。
普通のユーザーがそのような暴挙を犯すことはないだろうが、ChatGPT-4oのような高性能LLMの開発を目的とする事業者であれば話が別である。その点で、OpenAIが最も恐れた事態が今回のDeepSeek騒動と言えるかもしれない。
DeepSeek-R1のリリース
2025年1月20日、中国のAI開発スタートアップDeepSeekが、新たな推論モデル 「DeepSeek-R1」 を発表した。記事の冒頭で触れたように、このモデルはOpenAI-o1に匹敵する高性能なモデル（DeepSeek-R1、アプリ内では “DeepThink” とラベルされている）がチャット経由でなんと無料で利用できる。UIはほとんどChatGPTのものと変わらない。
🚀 DeepSeek-R1 is here!
⚡ Performance on par with OpenAI-o1
📖 Fully open-source model & technical report
🏆 MIT licensed: Distill & commercialize freely!🌐 Website & API are live now! Try DeepThink at https://t.co/v1TFy7LHNy today!
🐋 1/n pic.twitter.com/7BlpWAPu6y
— DeepSeek (@deepseek_ai) January 20, 2025
API価格は破格で、2025年2月上旬現在の価格はOpenAI社の2割ほどに設定されている。この価格とUXを継続的に維持・両立できれば（アクセス禁止措置が取られるなどの場合を除き）OpenAI社やAnthoropic社などからシェアを奪い取り、ヘビーユーザーの囲い込みが進むものと思われる。
| ChatGPT | Claude | DeepSeek | |
| 入力トークン (/1M tokens) | $2.50 | $3.75 | $0.55 |
| キャッシュされた入力トークン (/1M tokens) | $1.25 | $0.30 | $0.14 |
| 出力トークン (/1M tokens) | $10.00 | $15.00 | $2.19 |
公式のドキュメントによると、先ほど紹介したAIMEなどの競技数学においてOpenAI-o1に匹敵するスコアをマークしていると報告されている。
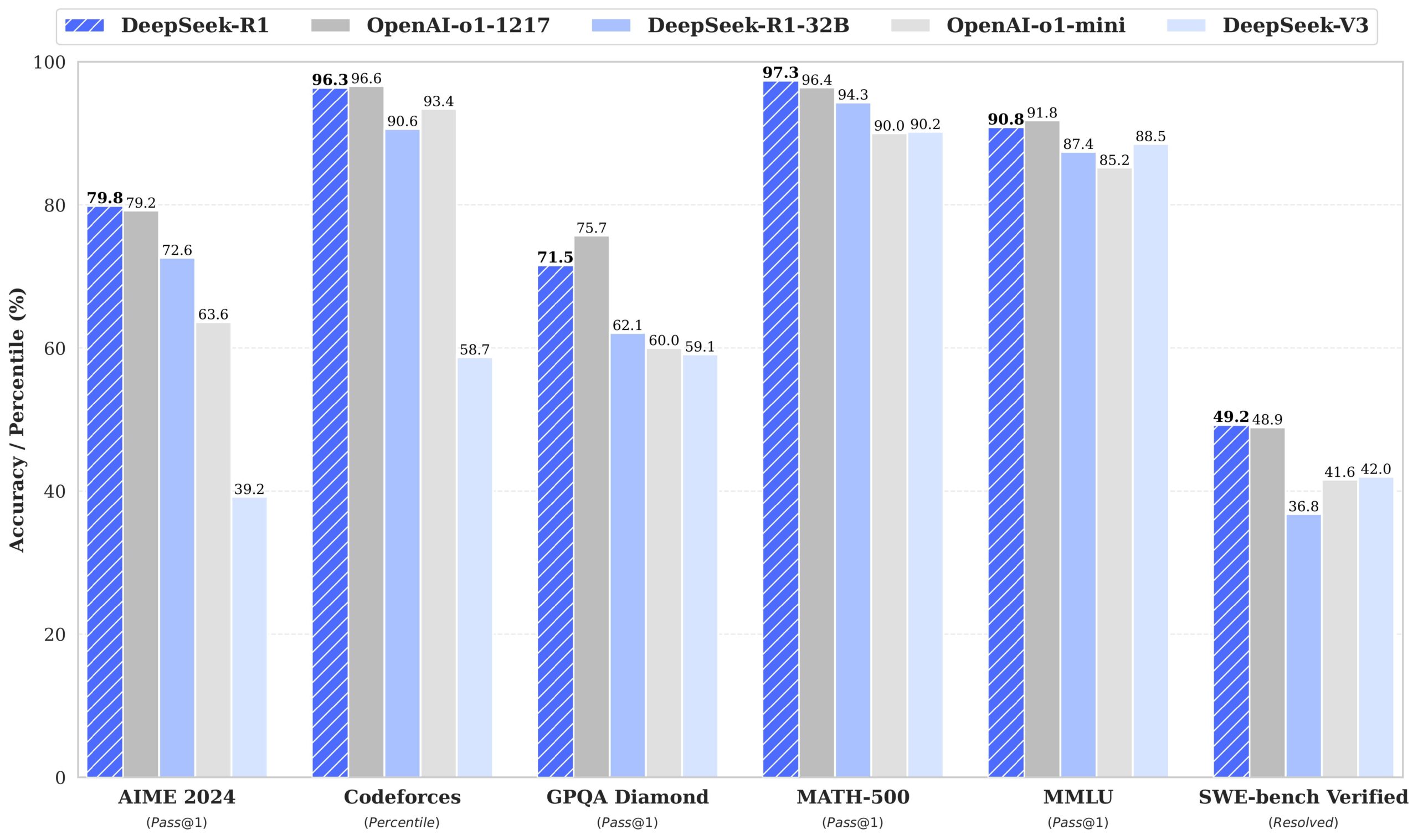
DeepSeek-R1は “Mixture of Experts”（MoE）として構築された671B（6710億）パラメータのモデルで、推論時にはそのうちの5.5％である37B（370億）パラメータのみが活性化するように設計されており、ここが計算コスト抑制に寄与しているとされる。
“Mixture of Experts” とは、モデルの特定部分（「エキスパート」と呼ばれる）を必要なときだけ動作させる仕組みで、計算コストを5割以上削減できる手法として知られる。通常のMoEでは数～十数程度のエキスパートからなるが、DeepSeek-R1では強化学習アルゴリズムや学習時のGPU効率を最適化することで256ものエキスパートを効率的にトレーニングすることに成功している。
全体としては1つの共有エキスパート（shared expert）が256のエキスパート（routed experts）から8つをルーティングし、協働して推論が行われる。257のうち9のエキスパートのみが稼働するため、6710億ものパラメータを持ちながらも推論時には全体の数％のパラメータしか利用しなくて済む。これがDeepSeekの経済性の源泉である。
また、DeepSeek-R1のトレーニングにはGRPO（Group Relative Policy Optimization）という
非公開ではあるが、DeepSeekのトレーニング時にはCUDAカーネルのカスタマイズ等を含むアセンブリレベルのGPUおよびメモリ利用効率のチューニングが行われているとみられる。また、計算効率を向上させるため、FP8（8-bit浮動小数点）のレベルでニューラルネットワークの学習が行われており、精度を維持するために様々な工夫が施されている。技術的な詳細はDeepSeek-V3の公式ドキュメントの3.2節に記載されているので参照していただきたい。
DeepSeek-R1に関する技術的な報告や解説は既に大量に存在しているので、技術的な詳細についてはそちらを参照していただきたい。基本的には公式ドキュメントが最も詳しい。R1のアーキテクチャはDeepSeek-V3ベースなので、仕組みについてはV3のテクニカルレポートを参照するのが良いだろう。
学習方法について詳しく知りたい場合はR1のテクニカルレポートを参照していただきたい。
また、以下にその他の主な日本語の文献を挙げておく。これら以外にも参考になりそうな文献をご存じの方はコメント欄で共有していただければ幸いである。
LLMチューニングのための強化学習：GRPO（Group Relative Policy Optimization）
めんだこ 氏, 2025/01/26公開
DeepSeek-R1の論文読んだ？【勉強になるよ】
asap 氏, 2025/01/27公開
ここでDeepSeek社についての情報を簡単にまとめておく。
DeepSeek（深度求索）の設立年は比較的最近の2023年7月17日で、中国・杭州に本社を置く企業であり主に大規模言語モデル（LLM）の開発を手掛けている。創業者でありCEOを務める梁文锋（Liang Wenfeng）氏は、中国のヘッジファンド「幻方量化（High-Flyer）」の共同創設者でもある。ヘッジファンドで荒稼ぎした資金を元手に、AI・LLM構築事業に乗り出したそうである。
梁氏は浙江大学で電子情報工学の学士号（2007年）と情報通信工学の修士号（2010年）を取得。卒業後は成都に移り、AIの多様な応用を試みた後、金融分野での成功を収めた。2016年2月、梁氏はエンジニアの同級生2名と共に、数学とAIを活用した投資を行うヘッジファンド「High-Flyer」を共同設立、2019年までに資産運用額が100億元以上（約2000億円）の規模に成長しており、現在では1000億元を超えている。
2023年5月、梁氏はHigh-FlyerのAI研究部門を拡大し、人工汎用知能（AGI）の開発を目指すDeepSeekを設立した。2024年の1月、同社は効率的かつ低コストで大規模言語モデルを開発し注目を集めている。同社への注目が高まったのと同じ時期に梁氏が李強首相主催のシンポジウムに招待され、政府の政策立案に意見提供したことが報道されて話題となった。
DeepSeekには中国国内の有名大学出身者が多く在籍しており、高度な研究開発が行われているとされる。米国の AI スタートアップに対抗しうる国内の有力AI企業が登場したことを受けて、習近平指導部は自国の科学教育の正当性を誇示したいものと思われる。
DeepSeek-R1は2024年12月に公開されたDeepSeek-V3の後継で、推論コストの安さはDeepSeek-V2が公開された2024年5月の時点で既に話題になっていた。低コストで高性能なモデルを立て続けに発表している躍進ぶりを受けて、先行する米国のAI開発企業からは学習データの出所について疑問視する声が上がっている。これは要するに、自社のLLMがそっくりそのままコピーされているのではないか、という疑念の目を向けているということである。
個人的な使用感ではあるが、DeepSeekは出力結果の精度やレスポンスの速さ等の点でChatGPTの競合となりうるポテンシャルを持っているように思われる。ただ、記事執筆時点でのDeepSeekは時間帯によっては動作がやや緩慢で、サーバーがビジー状態だとして応答しなくなるタイミングが複数あった。後の報道でDeepSeekのサーバーがアメリカを発信源とするサイバー攻撃を受けていたことが明らかになった。攻撃者が何者かは不明であるが、サイバー空間では米中間で既に小競り合いが行われているようである。
「知識の蒸留」とは何か
LLMを精度よく「模倣」する技術の一つとして「知識蒸留」という技術が知られている。知識蒸留（Knowledge Distillation, KD）という概念は、Hintonらが2015年に発表した論文「Distilling the Knowledge in a Neural Network」 によって広く知られるようになった。これは高性能な大規模モデル（教師モデル, Teacher Model）の知識を、より小型のモデル（生徒モデル, Student Model）へ移し、計算コストを削減しつつ性能を維持する手法である。
実際、OpenAIは「Model Distillation」という機能を導入し、運用中のLLMのコスト削減に成功している。この手法では、大規模モデルの出力を活用して、小規模なモデルを効果的にトレーニングし、推論コストを大幅に削減している。（参考：OpenAIの蒸留機能(Model Distillation)を使って運用中のLLMのコストを削減する取り組み）
知識蒸留は深層学習モデルを軽量化するためのテクニックとして提案された手法だが、生徒モデルは必ずしも「小さいモデル」である必要はなく、異種アーキテクチャへの知識転移（例：TransformerからCNNへ）や同じサイズのモデル間での性能向上にも応用される。（参考：深層学習モデル軽量化技術まとめ – Nurkic）
OpenAIのGPT-4やo1などのモデルではAPI経由で入出力できるため、「ブラックボックス蒸留（Black-box distillation）」と呼ばれる手法を用いることができる。これは、モデルの中身が不明（ブラックボックス状態）でも入力と出力のペアを多数収集し、蓄積したデータを教師データとして元のモデルに近づくよう学習させるというリバースエンジニアリング的な手法である。
なお、スタートアップ企業や学術機関がChatGPTのような商用LLMの出力を使用して別のモデルをトレーニングすることは一般的に行われているということも付け加えたい。智譜AI（Zhipu AI）や月之暗面（Moonshot AI）といった中国の有名なAI企業でも、ChatGPTのAPIを使ってデータセットを構築して自社モデルの学習に利用したとされる例が報告されている。
私見
DeepSeekがOpenAIのモデルを「模倣」した痕跡は認められるものの、全ての学習においてOpenAIのモデルのみがリファレンスになっている可能性は低そうである。恐らく、DeepSeekはOpenAI社のみをターゲットにはしておらず、その他の生成AIモデルに対しても知識蒸留を行ったものと考えられる。最も品質の高いデータを多数収集出来てしまったという点で、トレーニングの過程でOpenAIのモデルが必然的にメインターゲットとなった、というのが実際のところではないだろうか。
余談だが、実は少なくない生成AIが「自分はChatGPTである」と誤認識しているという事実がある。モデルによっては「あなたはOpenAIによって訓練されたモデルですか？」と尋ねると、全く事実と異なるにもかかわらずこれを肯定する回答をすることがあるそうだ。ネット上の多種多様な文章の中にはChatGPTが出力したものも多く含まれている。こうしたテキストを大量に学習することでモデル自身がChatGPTであると勘違いしてしまうという現象が知られている以上、（OpenAIとMicrosoftは確固たる証拠があると主張しているが）憶測だけでDeepSeekを非難するのは避けておくのが賢明かもしれない。
（参考）ディープシークの新AIモデルがChatGPTを名乗る理由
AIソリューションオフィス 2024年12月28日 12:16
以下の理由から、このような「キメラ的AIモデル」は今後も増えていくと思われる。
-
- DeepSeekのモデルがオープンソースで公開されていること
- アーキテクチャと学習方法の概要が論文として公開されていること
- 良質な訓練データ、もしくは良質な先行LLM（またはデータセット）にアクセスできれば、型落ちのGPUでも高品質なAIモデルを安く構築できること（および、その事実を全世界に公開したこと）
MetaのLLaMAがオープンソースで公開されたように、誰でもDeepSeekの技術をベースにして独自のLLMを作れる環境が整った。これにより（良質な訓練データの確保という課題はあるにせよ）参入障壁が下がったのは間違いないだろう。
アーキテクチャと学習方法の詳細が公開されたことで、他の研究者や企業がDeepSeekの手法を模倣・改善しやすい環境が生まれている。実際、DeepSeek社はAI技術の民主化を理念に掲げており、昨今「AIのブラックボックス化」が進む中で、新たなAIモデル開発の指針となり得る。
DeepSeekの成功の核心部分は、最新のGPUを使わずとも「良質な訓練データ」があれば工夫次第で高性能なAIを作れることを証明した点であろう。既存の商用LLMに対する知識蒸留という法的にグレーな飛び道具が使用された可能性はあるが、廉価版GPUでモデル構築できたことはAI開発の分散化・民主化を後押しする成果と言える。
ところで、仮にOpenAI社がDeepSeek社の不正を暴いたとして、DeepSeekを相手に訴訟を起こすことはどれだけ妥当であろうか？
OpenAIはChatGPT-4oやo1などの構築に既存の著作物を大量に（場合によっては不正に）利用している可能性が指摘されている。自社の行為を棚に上げてモデルにタダ乗り（タダではないが）した後発企業を責めるというのはお門違いではないか、という意見もある。
また、そもそもパブリックドメインのテキストを大量に学習させているモデルがオープンソースになったところで、結局人々が享受できる知識はパブリックドメインの知識そのものと言えるので「あるべきものがあるべきところに帰っただけ」という意見も存在する。
とはいえ、OpenAI社は莫大なコストをかけて自社のモデルを開発している以上、自社のモデルが蒸留されることに対して反発するのは自然なことだろう。今回のDeepSeekのように優れたモデルを蒸留して、より経済的かつ高性能なモデルを構築できることが明らかになった以上、効率的な強化学習手法を利用した後追いでのAI開発が流行すると考えられる。
DeepSeekがオープンＡＩから「蒸留」した証拠あり－米政府ＡＩ責任者 – Jackie Davalos, 2025/01/29公開
DeepSeek狂奏曲
清水亮, 2025/01/30公開
ところで、DeepSeek以外のチャット系LLMがお行儀よく開発されてきたかというと、別にそんなことは無い。OpenAI社はパブリックドメインのテキスト以外にも、著作権を無視して大量の著作物を学習データとして利用したと言われているし、Anthoropic社のClaudeもChatGPTを教師データにしてパクった参考にしたと言われている。実際のところ、こうした開発の裏事情の真偽は不明であり、今後も明らかになることは無さそうである。
余談①：言語モデル関連技術のマイルストーン
2017年頃から現代にかけての生成AIの進化においては、幾つかの重要な出来事が存在する。以下に主要なものを簡潔にまとめた。
-
- 2017年：トランスフォーマーの登場（Transformer）：
Googleの研究チームが「Attention Is All You Need」（2017）を発表し、Transformerアーキテクチャを提案。それまでのRNN（リカレントニューラルネットワーク）やLSTM（長短期記憶）は長文を処理するのが苦手だったが、Transformerは「自己注意機構（Self-Attention）」を活用することで長文であっても文脈を正確に捉えられるようになった。この論文は機械学習研究の金字塔的な成果としてよく知られている。 - 2018年：BERT（文脈理解の強化）
2018年10月にGoogleが「BERT（Bidirectional Encoder Representations from Transformers）」を発表。双方向の文脈を考慮できるようになり、検索エンジンや機械翻訳が飛躍的に向上。翌年にはGoogleの検索エンジンに組み込まれた。自然言語処理の基礎が - 2020年：GPT-3（本格的な生成AIの実用化）
OpenAIが「GPT-3」を発表。生成AIの時代が本格的に始まる。1750億パラメータの巨大なモデルで、人間と同等レベルの文章生成が可能となった。 - 2022年〜現在：ChatGPTと次世代AIの登場
2022年11月にOpenAIがChatGPTを公開。全世界で瞬く間に普及し、一般ユーザーが手軽に生成AIを利用できる時代となった。現在はGoogleのGemini、AnthropicのClaudeなど多くの競合が登場しており、AI業界は混戦状態を呈している。
- 2017年：トランスフォーマーの登場（Transformer）：
2024年のノーベル物理学賞は「人工ニューラルネットワークによる機械学習を可能にした基礎的発見と発明に対する業績」に対して、John J. Hopfield氏、Geoffrey E. Hinton氏の両氏に送られた。化学賞は「タンパク質の構造予測および設計に関する業績」に対して、David Baker氏、Demis Hassabis氏、John M. Jumper氏の3名に授与された。歴史あるノーベル賞において同じ年に2つの分野で人工知能に関する研究成果が取り上げられたことは、AIドリブンでの科学の発展という新たな時代の幕開けの象徴となった。
今後、よりAI技術が発達した世界では、AIが科学の発展に必要不可欠な存在になると考えられる。今回のDeepSeekの躍進もその時代の一幕に過ぎないと言えよう。
余談②：DeepSeekの活用について
CyberAgent社が日本語のデータを使ってDeepSeek-R1を蒸留したモデルを公開した。現在、これを個人がローカル環境で動かしたとの報告を多数見つけることができる。ある程度のGPU環境があればハイエンドでなくともこれほどのモデルを動かせるというのは画期的なことと言える。
cyberagent/DeepSeek-R1-Distill-Qwen-32B-JapaneseをDatabricksで動かしてみる
@taka_yayoi, 2025/01/28公開
一方で、(再)蒸留の影響によるコーディング能力の低下も指摘されており、さらなるチューニングが待たれる。
CyberAgentが蒸留したDeepSeek-R1を試す
shi3z, 2025/01/28公開
また中華製LLMということもあって、機密情報が中国国内に漏洩する危険が無視できない。DeepSeekのアナウンスによるとユーザーから提供された情報は「自社のサーバー上に安全に保管されている」とのことだが、中国当局が同社のサーバーに自由にアクセスできないという保証はない。
ChatGPTの利用規約にはユーザーから提供された情報が学習データの一部として用いられる旨の記載がある（無料版の場合）。特に企業の場合、個人情報や特許、財務などに関する社外秘情報を入力することは致命的な損害を招きかねない。もしDeepSeekを利用する場合は、入力する情報の取り扱いに今まで以上に慎重になった方が良さそうである。
生成 AI の利用で最も使われる部類の一つがコーディング支援であろう。最近ではプロダクト開発においていわゆる “Vibe Coding” が主流となりつつある。IT 業界でAIを使わずに仕事するのは、もはや時代遅れと言わざるを得ない状況になってきている。
使う AI のモデルはDeepSeekに限られるわけではないが、DeepSeekは米国産の他のモデルに比べてプログラミング性能は遜色ないとされている。今後より優れたモデルが登場するはずなので、一時の評価のみで使用の可否を判断してしまうのはややもったいないかもしれない。