モンテカルロ法は乱数を利用する数値計算法であり、様々な場面で応用することができる重要な手法です。プログラミング実習などでも扱われることが多く、理屈をしっかり理解しておくことは大切です。本稿ではモンテカルロ法によるサンプリングを用いて円の面積（円周率）を求めてみます。参考用のRubyやPythonのコードも掲載しています。
モンテカルロ法とは
「モンテカルロ法」とは、乱数を用いた試行を繰り返すことで、ある問題に対する近似解を数値的に求める、という手法のことです。因みに「モンテカルロ」とはフランス南部の地中海沿岸に位置するモナコ公国の首都であり、カジノやモナコグランプリなどで世界的に有名な保養都市の名前です。モンテカルロ法はアメリカの科学者ジョン・フォン・ノイマンによって名付けられたとされる数値シミュレーション法で、モンテカルロが賭博の中心地であることに因んでいます※注1。
※注1：やや脱線しますが、実はこの「モンテカルロ法」の原理はかつてアメリカの軍事機密(！)でした。1940年代のアメリカでは電子計算機”ENIAC”を開発するプロジェクトが極秘で行われており、その中でモンテカルロ法の原型となる考え方がアメリカの科学者スタニスワフ・ウラムによって考案されました。この方法は軍事的に重要な手法とされ、これを指すコードネームを考える必要がありました。ノイマンはウラムの同僚として働く中で、ウラムの叔父が親戚からお金を借りてまでモナコのモンテカルロカジノでギャンブルをしていたという話を聞いていました。ノイマンはこの話から着想を得て「モンテカルロ法」と名付けたと伝えられています。ギャンブルも立派な(？)数学の１つと言えますし、なかなか洒落たネーミングですね！
図１．モナコ公国の首都「モンテカルロ」
● ● ●
さて、モンテカルロ法の概要は次の通りです。
ある図形$F$の内部に含まれる点の数を$n$、サンプリングした点の総数を$N$とし、図形$F$を含む面積$S’$の領域内でサンプリングを行ったとすると、次の式によって図形$F$の面積$S$を求めることができます。$$S=\dfrac{n}{N} \times S’$$
これは即ち、全体の面積に対してその図形の面積がどれだけの割合を占めているかを求めていることになります。確率とは全事象に対する特定の事象が起こる割合のことなので、サンプリングする点が十分ランダムに取れるのであれば、面積についても同様の原理で計算が可能という訳です※注2。
※注2：この「十分ランダムに」という点は恐らく皆さんが思っている以上に重要な要素です。乱数の生成方法に関してはそれだけで数学の１分野を成してしまうほど奥が深いのです･･･。
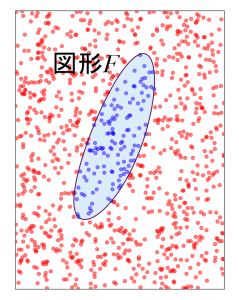図２．モンテカルロ法によるサンプリングの例
例として示した図２（範囲は$(0,0)$～$(3,4)$）の図形$F$は$$x^3+y^2-3xy+1<0$$を満たす第一象限上の領域なのですが、この面積の厳密値を計算するのは容易ではありません。このような場合には、モンテカルロ法のような数値的に近似解を得る方法が活躍します。モンテカルロ法による求積では、サンプリングする点の数を多くするか、サンプリングする領域をできるだけ狭くすると精度が向上します。
上記の図形について手元のプログラムで10万点のサンプリングを計10回行った結果の平均値は $1.48099…$ となり、100万点の場合は $1.49028…$ となりました。参考のため、厳密値が$$\int_{\large{\frac{1+\sqrt{33}}{8}}}^{2}\sqrt{\mathstrut -4+9 x^{2}-4 x^{3}}\, d x=1.48821…$$となることを付記しておきます。一般に、サンプリング回数が多ければ多いほど近似値は厳密値に近付きます。
※参考：「大数の法則」Wikipediaより
円の面積（円周率）の計算
それでは早速、円の面積（円周率）を求めてみましょう。
円の対称性から、四分円の面積を４倍すれば$\pi$になるので、第一象限上の領域（範囲は$(0,0)$～$(1,1)$）のみを考えれば十分です。以下、この領域を考えます。
試しに1000個の点をサンプリングすると、分布の様子は下図のようになりました。青色のプロットは円の中に入っている点、赤色のプロットは円の外側にある点を表しています。
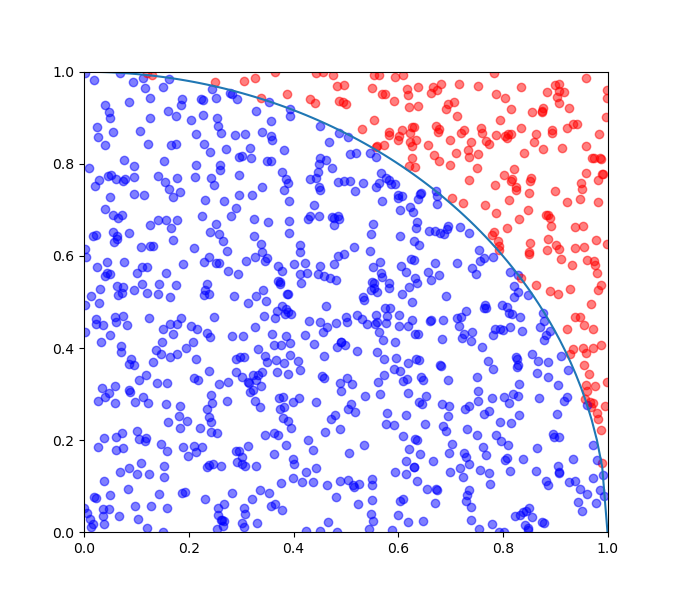図３．四分円のサンプリング（1000点）
この場合、四分円の中に入っている点の数$n$は$793$、サンプリングした点の総数$N$は$1000$なので、$n/N=0.793$ という値が得られます。つまり、この $0.793$ という近似値が四分円の面積 $\dfrac{\pi}{4}=0.785398…$ に相当します。
● ● ●
サンプリング回数をさらに増やしてみます。10000個の点をサンプリングすると分布の様子は下図のようになり、近似値 $0.7852$ が得られました。1000点の場合と比べると、平均して精度が1～2桁向上します。
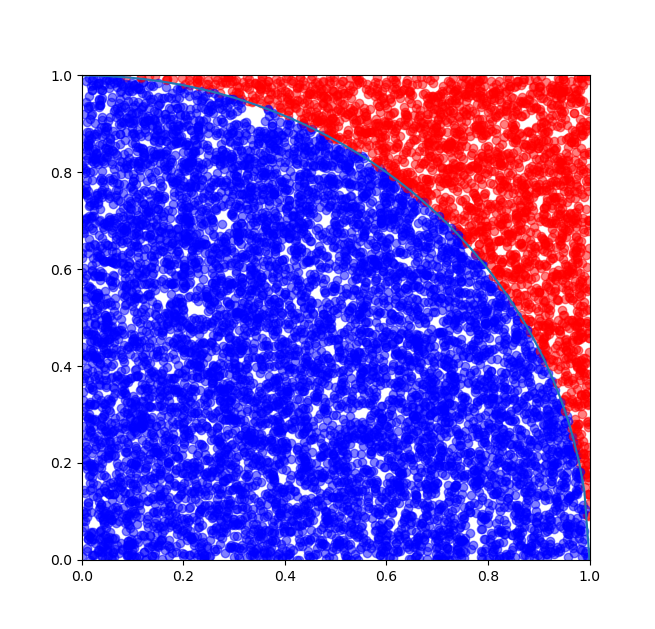図４．四分円のサンプリング（10000点）
図３に比べてプロットがより密になっているのが分かると思います。$0.7852 \times 4=3.1408$ なので、円周率が小数点以下$2$桁まで求められています。
モンテカルロ法では、このようにして面積を数値的に求めることができるのです。
● ● ●
参考までに、Pythonのサンプルのコードを置いておきます。numpyやmatplotlibを使っていない人は適宜書き換えてください。
import numpy as np
import matplotlib.pyplot as plt
# サンプリングする回数
total = 1000
# 乱数を生成
x = np.random.rand(total)
y = np.random.rand(total)
i = 0
# 領域の境界線を描画
t = np.linspace(0, 1, 100)
plt.plot(t, np.sqrt(1-t*t))
# 領域内の点を数える変数
count = 0
while i < total:
if y[i]*y[i] < 1 - x[i]*x[i]: # 領域内に含まれるかどうかの判定
count = count + 1
plt.scatter(x[i], y[i], alpha=0.5, color='blue')
else:
plt.scatter(x[i], y[i], alpha=0.5, color='red')
i = i + 1
# 面積を出力
print(count/total)
# プロットを範囲指定して出力
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.show()
※点に透明度を設定したくない場合はalphaの部分を消して下さい。また、画像を出力したくない場合は最後の部分をコメントアウトして下さい。PCのスペックにもよりますが、1万点以上のプロットには時間が掛かるので要注意です。
Rubyの場合は次のようになります（画像は出力されません）。
total = 1000
i = 0
count = 0
while i < total
x = rand
y = rand
if( x**2 + y**2 < 1 )
count = count + 1
end
i = i + 1
end
# 面積を出力 (to_fメソッドを付けないと剰余計算になるので注意)
puts((count.to_f/total.to_f))
面積計算への応用例
典型的な応用例として、もう１つ図形の面積を求めてみましょう。
原点$(0,0)$を中心とする半径$1$の円と、点$(1, 0)$を中心とする半径$1$の円の重なり部分の面積をモンテカルロ法で求めてみます。$x$軸に関する対称性から、こちらも下図のように第一象限上の領域だけを考えればよく、得られた値を２倍すれば求める値となります。
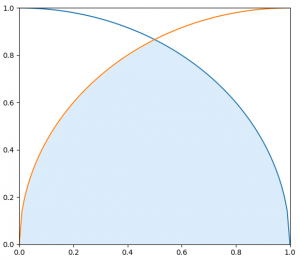図５．重なり部分の上半分
試しに1000個の点をサンプリングすると、分布の様子は下図のようになりました。青色のプロットは重なり部分の中に入っている点、赤色のプロットは重なり部分の外側にある点を表しています。
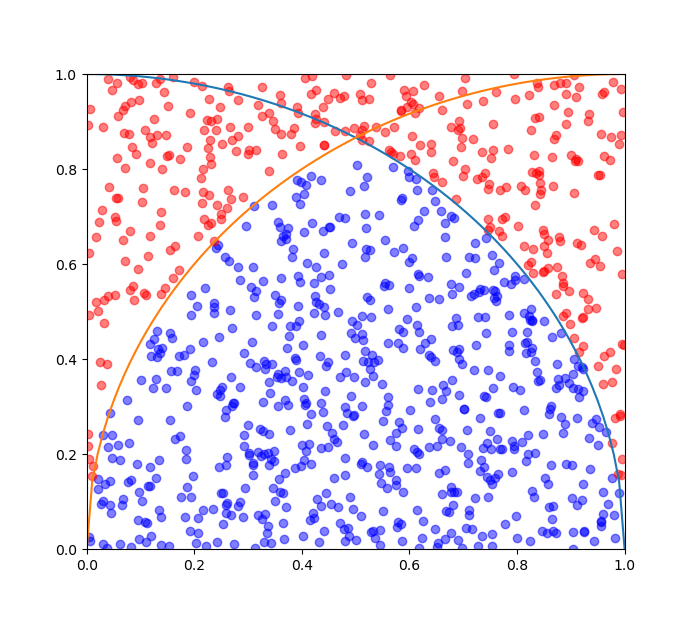図６．重なり部分のサンプリング（1000点）
近似値として $1.212$ という値が得られました。さらにサンプリング数を10000点に増やすと $1.2272$ が得られました。なお、厳密値は$$\frac{2}{3}\pi-\frac{\sqrt{3}}{2} \approx 1.228369…$$で与えられます。
● ● ●
余談ですが、この面積計算について、管理人はユニークな勘違いに遭遇した経験があります。いつぞやのプログラミング実習中、ある学生の方が次のような考え方でこの面積を求めていました。
考え方（？）
ある点を$(0,0)$～$(1,1)$の領域でランダムにプロットしたときに、原点$(0,0)$を中心とする半径$1$の円（青色の円）に含まれる確率と、点$(1, 0)$を中心とする半径$1$の円（オレンジ色の円）に含まれる確率は等しい。
したがって、求める確率は結局「青色の円に含まれる確率の２乗」に等しくなる！
一見、合理的に見えなくもない解き方ですが、これは残念ながら誤った発想です。確かにこの主張の前半部分は正しいのですが、後半部分が正しくありません。
しかし一方で「青色の円に含まれる確率の２乗」は $\dfrac{\pi^2}{16}$ なので、これを２倍すると$$\dfrac{\pi^2}{8}=1.233700…$$となり、正しい値に近い値となっています。このことが余計に間違いを気付きにくくする要因になっていたのでした。
プログラム（機械）はコードに従って「正しく」結果を出力しますが、その結果自体が正しいものかまでは保証してくれません。プログラムによるミスというのは結局のところ、コードを書く側の人為的なミスによるものなのです。そのことに改めて気付かされた出来事でした。
● ● ●
以下に、Pythonのサンプルのコードを置いておきます。numpyやmatplotlibを使っていない人は適宜書き換えてください。
import numpy as np
import matplotlib.pyplot as plt
# サンプリングする回数
total = 1000
# 乱数を生成
x = np.random.rand(total)
y = np.random.rand(total)
i = 0
# 領域の境界線を描画
t = np.linspace(0, 1, 100)
plt.plot(t, np.sqrt(1-t*t))
plt.plot(t, np.sqrt(1-(t-1)*(t-1)))
# 領域内の点を数える変数
count = 0
while i < total:
if y[i]*y[i] < 1 - x[i]*x[i] and y[i]*y[i] < 1 - (x[i]-1)*(x[i]-1): # 領域内に含まれるかどうかの判定
count = count + 1
plt.scatter(x[i], y[i], alpha=0.5, color='blue')
else:
plt.scatter(x[i], y[i], alpha=0.5, color='red')
i = i + 1
# 面積を出力（第四象限の部分も考えて2倍している）
print(2*count/total)
# プロットを範囲指定して出力
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.show()
Rubyの場合は次のようになります。
total = 1000
i = 0
count = 0
while i < total
x = rand
y = rand
if( x**2 + y**2 < 1 and (x-1)**2 + y**2 < 1 )
count = count + 1
end
i = i + 1
end
# 面積を出力 (2倍していることに注意)
puts(2*(count.to_f/total.to_f))
サンプリングする回数をやたらと大きくしてしまうとプログラムが止まったように見えることがあります。ウンともスンとも言わない場合は「Ctrl+C」で早めに中断しましょう･･･。