今回は灘中学校の入試過去問から図形に関する問題を取り上げます。たかが中学入試と侮るなかれ、シンプルながらも面白い一題です。言われてしまえばアッという間に解けてしまいますが、高校生に出題しても解けない人が出てくるような良問です。
灘中の問題
次のような問題を考えます。
問題
合同な2つの三角形を右の図のように置きます。このとき、$\mathrm{AB}$の長さは $\boxed{ }$ cm です。
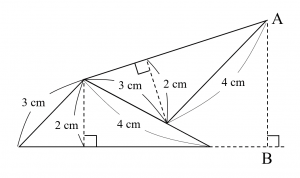
まずは少し考えてみて下さい。高校生に解かせると解き方が色々と思いつくためか、案外出来が悪かったりします。
簡単な解法
最もシンプルな解き方は相似を使う方針でしょう。
下の図のように辺を延長するように補助線を引いてみます。すると角度の関係から網掛けで示した二つの三角形は互いに相似であることがわかります。
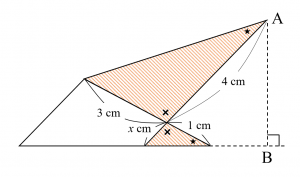
揃えて図にすると次のようになります。
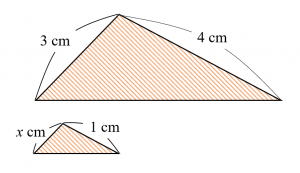
これより、$$3:4=x:1$$ $$\therefore x=\dfrac{3}{4}$$と求められます。
次に、下図のように直角三角形を考えます。これらも2角相等(2組の角がそれぞれ等しい)により、相似です。
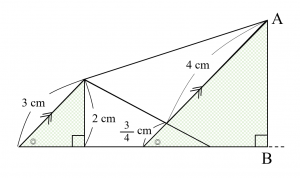
斜辺:高さの比を考えて、$$3:2=4+\dfrac{3}{4}:\mathrm{AB}$$ $$\therefore \color{red}{\mathrm{AB}=\dfrac{19}{6}=3\dfrac{1}{6}}$$を得ます。これが答えです。特に問題文に指示が無いので、帯分数で書いていなくても減点はされません。
いかがでしょうか? 言われてみると、あっさり解けてしまいますよね。
発展的な改題
では、さらに三角形を積み上げた場合、高さ$\mathrm{CD}$はどうなるでしょうか?
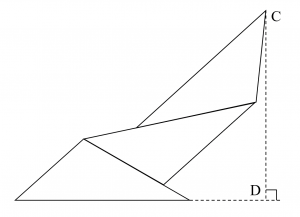
三角形の形は先程のものと同じで、三角形はいずれも互いに合同とします。
答えにはルートが出てくるので、中学生(高校1年生?)向けの問題です。
さて、この場合も補助線を引いて解決可能です。元の三角形の底辺の長さを$y$とすると、相似比から辺の長さが図のように求められます。
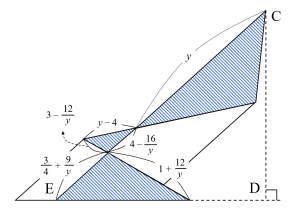
斜線掛けされている3つの三角形はいずれも相似です。それぞれの相似比から線分$\mathrm{CE}$の長さは$$\small \left(\dfrac{3}{4}+\dfrac{9}{y}\right)+\left(4-\dfrac{16}{y}\right)+y=\dfrac{19}{4}-\dfrac{7}{y}+y$$と求められます。
よって、線分$\mathrm{CD}$の長さは線分$\mathrm{CE}$の$\dfrac{2}{3}$倍なので、$$\mathrm{CD}=\dfrac{19}{6}-\dfrac{14}{3y}+\dfrac{2}{3}y$$となります。
最後に、底辺の長さ$y$を求めます。2つの直角三角形で三平方の定理を使いましょう。
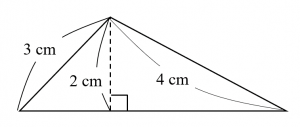
すると、$$y=2\sqrt{3}+\sqrt{5}$$となりますので、$$\small \begin{align} \mathrm{CD} &= \dfrac{19}{6}-\dfrac{14}{3}\cdot\dfrac{1}{2\sqrt{3}+\sqrt{5}}+\dfrac{2}{3}(2\sqrt{3}+\sqrt{5}) \\ &= \dfrac{19}{6}-\dfrac{14}{3}\cdot\dfrac{(2\sqrt{3}-\sqrt{5})}{12-5}+\dfrac{2}{3}(2\sqrt{3}+\sqrt{5}) \\ &=\dfrac{19}{6}-\dfrac{14}{21}(2\sqrt{3}-\sqrt{5})+\dfrac{14}{21}(2\sqrt{3}+\sqrt{5}) \\ &= \dfrac{19}{6}+\dfrac{28\sqrt{5}}{21} \\ &= \color{red}{\dfrac{19}{6}+\dfrac{4\sqrt{5}}{3}} \end{align}$$と求められます。
今回は先に原題を紹介していたので解答の方針には困らなかったでしょうが、こちらの改題の方を初見で出されたら詰まる人が多く出てくるような気がします。
効果的な補助線が引けるように普段から練習しておきたいですね!
(コメント)
灘中の問題には高校入試並みの問題が出題されることがあります。本問は相似の関係を使わないと解けませんので、一般的な小学6年生にとっては発展的な内容と言えます。本問のような図形問題は着眼点が悪いと余計な時間を取られてしまいます。試験場では問題を色々な視点から観察できる柔軟さがとても大切です。
