【数Ⅲ】三角関数の極限公式の証明

今回は数Ⅲ微積の基本となる三角関数の極限公式の証明を掲載します。

 

 $\small \displaystyle \lim _{x \rightarrow 0} \dfrac{\sin x}{x}=1$ の証明

これは三角関数の微分に必要な重要な公式です。この式は以下のような円弧$\mathrm{OAB}$を用いて図形的に証明可能です。因みに、この証明は2013年の大阪大理系で出題されたことがあります。

下図の三角形や扇形の面積について$$\triangle \mathrm{OAB} < \text { 扇形 } \mathrm{OAB} < \triangle \mathrm{OAT}$$が成り立ちます。

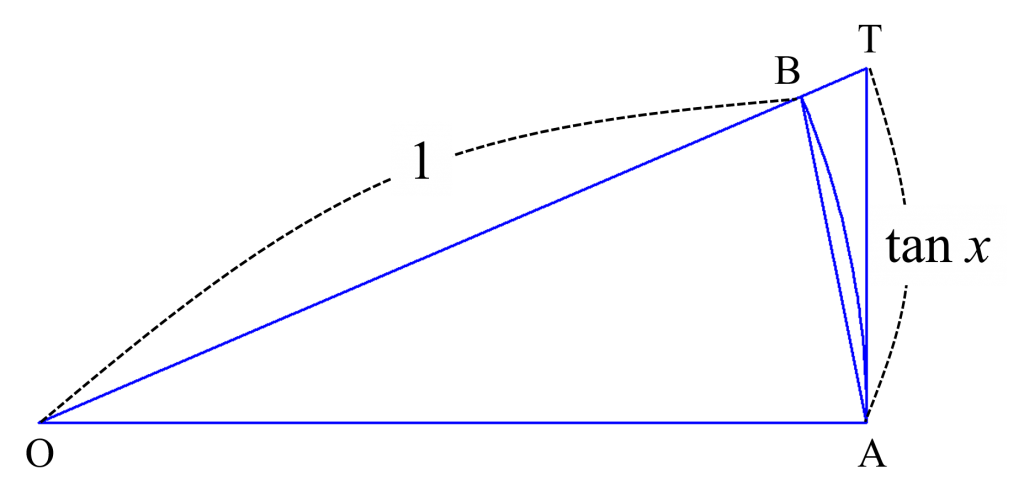
そこで、$\angle \mathrm{AOB}=x$ とすると、三角形および扇形の面積について$$\small \frac{1}{2} \cdot 1 \cdot 1 \cdot \sin x<\frac{1}{2} \cdot 1 \cdot 1 \cdot x<\frac{1}{2} \cdot 1 \cdot \tan x$$が成り立つので、$$\sin x<x<\tan x$$となります。逆数を取ると$$\frac{1}{\tan x}<\frac{1}{x}<\frac{1}{\sin x}$$となるので、辺々に$\sin x$を掛けて$$\cos x<\frac{\sin x}{x}<1$$を得ます。$\displaystyle \lim _{x \rightarrow+0} \cos x=1$ となるので、はさみうちの原理から、$$\displaystyle \lim _{x \rightarrow +0} \dfrac{\sin x}{x}=1$$が成立します。$x$が負のときは $t=-x$ などと置き換えれば同様の不等式から示せます。以上より、$$\displaystyle \lim _{x \rightarrow 0} \dfrac{\sin x}{x}=1$$が示されます。ここから $\displaystyle\lim_{x\to0}\frac{\tan x}{x}=1$ も示されます。

 

 $\small \displaystyle \lim _{x \rightarrow 0} \frac{1-\cos x}{x^{2}}= \frac{1}{2}$ の証明

これは先ほどの公式を用いて次のように証明されます。$$\small \begin{aligned} \lim _{x \rightarrow 0} \frac{1-\cos x}{x^{2}} &=\lim _{x \rightarrow 0} \frac{1-\cos ^{2} x}{x^{2}(1+\cos x)} \\ &=\lim _{x \rightarrow 0} \frac{\sin ^{2} x}{x^{2}(1+\cos x)} \\ &=\lim _{x \rightarrow 0} \left(\frac{\sin x}{x}\right)^2\cdot\frac{1}{1+\cos x} \\ &= 1^2\cdot\frac{1}{1+1} \\ &=\frac{1}{2} \end{aligned}$$または次のように示すこともできます。$$\small \begin{aligned}
\lim _{x \rightarrow 0} \dfrac{1-\cos x}{x^{2}} &=\lim _{x \rightarrow 0} \dfrac{2 \sin ^{2} \dfrac{x}{2}}{x^{2}} \\ &=\lim _{x \rightarrow 0} 2\left(\dfrac{\sin \dfrac{x}{2}}{x}\right)^{2} \\ &=\lim _{x \rightarrow 0} \dfrac{2}{4}\left(\dfrac{\sin \dfrac{x}{2}}{\dfrac{x}{2}}\right)^{2} \\ &=\dfrac{1}{2} \cdot 1^{2} \\ &= \dfrac{1}{2}
\end{aligned}$$

このように半角の公式を使っても良いですが、$1-\cos x$ が式に含まれるときは $1+\cos x$ を掛けて不定形を解消するのが有効です。

 

 $\small \displaystyle \lim _{x \rightarrow 0} \dfrac{\sin 2x}{x}$ の値は？

一般に $\displaystyle \lim _{\bigcirc \rightarrow 0} \dfrac{\sin \bigcirc}{\bigcirc}=1$ が成り立つので、極限をとるときは$\bigcirc$の部分を揃えるように式変形します。$$\small \begin{align}
& \quad \lim_{x\to 0} \frac{\sin 2x}{x} \\
&=\lim_{x\to 0} \frac{\sin 2x}{2x}\cdot 2 \\
&=2 \end{align}$$

例えば $\small \displaystyle \lim_{x\to 0} \frac{\sin 2x}{\sin 3x}$ の場合は$$\begin{align}
& \quad \lim_{x\to 0} \frac{\sin 2x}{\sin 3x} \\
&=\lim_{x\to 0} \dfrac{\sin 2x}{2x}\cdot\dfrac{1}{\dfrac{\sin 3x}{3x}}\cdot \frac{2}{3} \\
&=\frac{2}{3} \end{align}$$のようになります。

 

 例題

（１）$\displaystyle \lim _{x \to 0} \frac{\sin x^{2}}{1-\cos x}$

（２）$\displaystyle \lim _{x \rightarrow 0} \frac{\sin x^{\circ}}{x}$

（３）$\displaystyle \lim _{x \rightarrow 0} \dfrac{\tan x-\sin x}{x^{3}}$

---