一昔前の岐阜大の入試から三角関数で囲まれた図形の回転体の求積に関する問題を取り上げます。シンプルながらも数Ⅲ分野頻出の回転体の基礎を確認できる良問です。
《問題》
$xy$ 平面上の2つの曲線 $y=\cos \dfrac{x}{2}$ $(0 \leqq x \leqq \pi)$ と $y=\cos x$ $(0 \leqq x \leqq \pi)$ を考える。以下の問に答えよ。
(1)上の2つの曲線、および直線 $x=\pi$ を描き、これらで囲まれる領域を斜線で示せ。
(2)(1)で示した斜線部の領域を$x$軸のまわりに1回転して得られる回転体の体積を求めよ。
(岐阜大学2003年 (医/工)第3問)
《考え方》
回転させるべき領域は(1)の領域を回転軸($x$軸)に関して折り返した図形になります。このことに注意して積分します。
回転体の体積計算では、
① 積分範囲を細かく分けて計算する
② ひとまず大きな回転体の体積を求めてから余分な部分の体積を削る
という2つのアプローチがとれます。計算に自信のある方は①の方法でも良いでしょうが、実用上は②の方が計算ミスを誘発しにくいのでオススメです。
解答例
(1)
$y=\cos \dfrac{x}{2}$ を青線、$y=\cos x$ を赤線で描くと、求める領域は以下の斜線部となる。
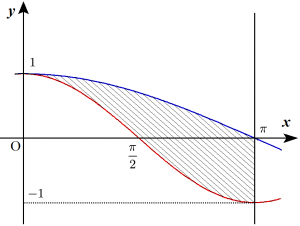
(2)
(1)の斜線部を$x$軸の周りに回転するということは、(1)の斜線部を$x$軸に関して折り返してできる領域を$x$軸の周りに回転することである。
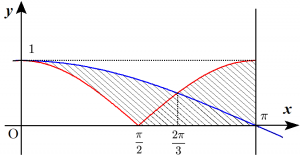
ここで、以下のように $0 \leqq x \leqq \pi$、$y \geqq 0$ の部分の図形を3つに分ける。
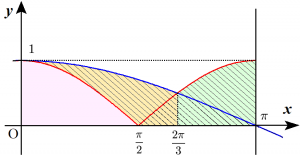
このとき「桃色+黄色」の回転体の体積$V_1$は、$$\small \begin{align}
V_{1} &=\pi \int_{0}^{\frac{2}{3} \pi}\left(\cos \dfrac{x}{2}\right)^{2} d x \\
&=\dfrac{\pi}{2} \int_{0}^{\frac{2}{3} \pi}(1+\cos x) d x \\
&=\dfrac{\pi}{2}[x+\sin x]_{0}^{\frac{2}{3} \pi} \\
&=\dfrac{\pi^{2}}{3}+\dfrac{\sqrt{3}}{4} \pi
\end{align}$$となる。「桃色」の回転体の体積$V_2$は、$$\small \begin{align}
V_{2} &=\pi \int_{0}^{\frac{\pi}{2}}(\cos x)^{2} d x \\
&=\dfrac{\pi}{2}\left[x+\dfrac{1}{2} \sin 2 x\right]_{0}^{\frac{\pi}{2}} \\
&=\dfrac{\pi^{2}}{4}
\end{align}$$となり、「緑色」の回転体の体積$V_3$は、$$\small \begin{align}
V_{3} &=\pi \int_{\frac{2}{3} \pi}^{\pi}(-\cos x)^{2} d x \\
&=\dfrac{\pi}{2}\left[x+\dfrac{1}{2} \sin 2 x\right]_{\frac{2}{3}\pi}^{\pi} \\
&=\dfrac{\pi}{2}\left(\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{4}\right) \\
&=\dfrac{\pi^2}{6}+\dfrac{\sqrt{3}}{8} \pi
\end{align}$$となるから、求める回転体の体積は$$\small \begin{align} V&=V_1-V_2+V_3 \\ &=\color{red}{\dfrac{\pi^2}{4}+\dfrac{3\sqrt{3}}{8} \pi} \quad \cdots (\text{答}) \end{align}$$となる。
(コメント)
(2)では積分範囲を細かく分けて計算することも可能ですが、計算ミスを抑えるために求め方を工夫しています。
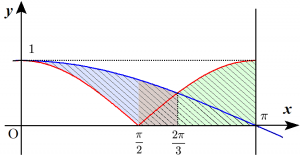
例えば以下のように領域を区切ることもできますが、分数計算が少し面倒になります。とはいえ、計算できないほど難しくなる訳ではないので好みの問題と言えるでしょう。