ここ数年～十数年のデータ科学の飛躍的な発展により、AIや機械学習が社会で広く認知され、利用されるようになりました。それに伴い、数理最適化の知識とそれを使いこなせる人材がこれまでになく求められる時代となっています。そこで管理人自身の知識整理も兼ねて【最適化問題の基礎】というシリーズで最適化手法についてまとめてみます。
今回は、最適化問題を解くために用いられる数理最適化とはそもそも一体何なのかについて解説していきます。
数理最適化は意外と身近
「最適化問題」とは変数、目的関数、制約条件といった要素を定義して、制約を満たしつつ目的の値を最大化／最小化する条件を求める問題です。最適化問題を数学的な手法によって解くことを「数理最適化」と呼んでいます。最適化問題は自然科学だけでなく社会科学など多種多様な分野のあらゆる所に潜在しており、解決すべき問題の多くは最適化問題に帰着できると言って良いでしょう。
最適化問題は学術分野だけでなく、私たちの日常生活においても沢山見つかります。例えば、
-
- 商品の仕入れをどうするか
- 限られた時間の中でどの観光地をどのルートで回るか
といった問題はまさしく最適化問題ですし、
-
- 300円の予算内でどのお菓子を遠足に持っていくか
なんかも立派な最適化問題です。この場合だと、
・変数：お菓子の種類と個数
・目的関数：お菓子の個数や満足度など
・制約条件：予算は300円以内
というイメージです。「変数」を色々と変えると「目的関数」の値も色々と変わります。「制約条件」を満たすように「目的関数」の値を最大（または最小）にするような「変数」の条件を探すというのが「最適化問題」です。
観光地巡りの際にGoogleマップにお世話になる人は多いと思いますが、目的地までのルートの提案はまさしく最適化問題の解そのものです。何時までに何処をどのルートで回るか、お土産をどこでどれだけ買うのか、…などなど、最適化問題と呼べるものは私たちの身近にあるのです。
（画像の一部を京都府タクシー協会のページから引用･改変）
「最適化問題」と聞くと何やら難しいように聞こえますが、このように考えると全然難しいことは言っていないのが分かりますよね。皆さんもそうとは知らずに最適化問題を日常的に解いているはずです。
現実社会において、数理最適化の手法は以下のような問題に応用されています。
・最適解･改善策を見つける
電力ロスを抑えた送電網の敷設、トラック配送効率の向上、工場の建設地の選定、スポーツの試合のスケジューリング、リターンを最大化する投資アドバイス、…など
・判断を自動化する
目的地までの最適なルート選択、最適な広告費の分配、勤務シフトの最適化、商品の需要予測、製品の品質の監視、不良品の選別、…など
こうした実際的な問題を数理最適化の手法で解決することは、最近流行りのデジタルトランスフォーメーション（DX）の使命の一つと言えるでしょう。ビジネスで発生する問題は大半が「組み合わせ最適化」の問題です。組み合わせ最適化とは、整数値などの離散的な要素を含む最適化問題を指しています。この分野では有名な「ナップサック問題」や「巡回セールスマン問題」などは組み合わせ最適化に分類されます。
一方で離散的な要素を含まない最適化は「連続最適化」と呼ばれます。連続な関数の極値を求める、多変数のモデル関数から最適値を予測する、などは連続最適化問題です。連続最適化は機械学習やシミュレーションなどの分野で欠かせない手法です。特に機械学習には画像認識や予測、パターン認識、自然言語処理など様々な用途があり、今後ますます需要が高まると予想される領域です。こうした分野では連続最適化の手法が重要となります。
数理最適化の手法
最適化問題は大きく分けると、離散的な対象を扱う「組み合わせ最適化」と、連続的な対象を扱う「連続最適化」に分類されます。両者では扱う問題の性質が異なるため、自ずと対処方法も変わってきます。以下に数理最適化の手法の例を列挙しておきます。
【組み合わせ最適化の例】
・力まかせ探索
・深さ優先／制限探索（19世紀～）
・幅優先探索（1940s～）
・動的計画法（1950s～）
・貪欲法
・均一コスト探索（1950s～）
・分枝限定法（1960s～）
・双方向探索（1970s～）
【連続最適化の例】
・直線探索
・最急降下法（1847～）
・共役勾配法（1952～）
・ニュートン法（ニュートン・ラフソン法）（17世紀～）
・準ニュートン法（DFP法、BFGS法…）（1960s～）
・ガウス・ニュートン法（19世紀～）
・内点法（1960s/80s～）
・Nelder-Mead法（1960s～）
・座標降下法
・進化的戦略（1960s～）
※括弧内はそのアルゴリズムが考案された大体の年代です（諸説あり）。あまり有用でないアルゴリズムも列挙しています。
最適化のアルゴリズムには種類が色々あるので、それぞれの問題に対して有効な手法をその都度選んで問題に適用することになります。組み合わせ最適化問題に対して、連続最適化の手法が有効であることはあまりありませんし、逆もまた然りです。
計算の「オーダー」
数理最適化と一口に言っても、何でもかんでもバッチリ上手くいく方法があるという訳ではありません。簡単な例として「巡回セールスマン問題」(traveling salesman problem、TSP) を考えてみましょう。
あなたはセールスマンです。外回りの営業で$n$件の顧客の元を訪問しなければなりませんが、でたらめに巡っていると余計な時間がかかってしまいます。そこで移動距離が最短になるような「最適な巡回路」を決定する必要があります。
これが巡回セールスマン問題の概要です。
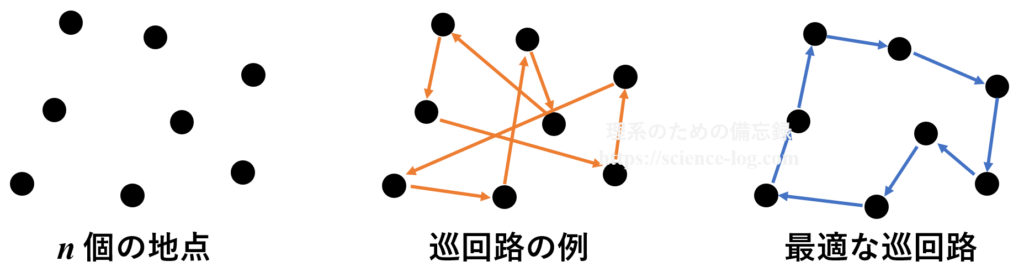
たったこれだけの問題？と思われるかもしれませんが、$n$の数が大きくなればなるほど厳密に解くのが難しくなります。巡回すべき地点の数を$n$とすると、可能な巡回路の総数は$\small \dfrac{n!}{2n}$通り存在します。$n$が比較的小さいときは全通りの組み合わせを調べることができますが、$n$が大きくなると巡回路の総数は途端に桁違いに増加します。
例えば、$10$地点の場合は巡回路の総数は$181440$通りですが、$30$地点の場合はおよそ$4.42×10^{30}$通りにまで膨れ上がります。
このように、考えるべき対象が増えると指数関数的に組み合わせが増えてしまい、元のアルゴリズムでは全く歯が立たなくなってしまうことがあります。このとき、計算量の「オーダー」は指数関数的であると言います（特に巡回セールスマン問題の場合は$n!$オーダーで計算量が増加するので、計算コストの点では指数関数より “悪い” です）。
※ただし、これはあくまでも全通りのパターンを数え上げた場合の話です。実際には効率的な探索アルゴリズムが知られており、$30$地点程度のTSPであれば現実的な時間内で解くことができます。
一般に計算の複雑さは、問題を解くのに必要な計算の手間（計算量）と、メモリの量（領域量）で決まります。アルゴリズムを設計する上ではどちらの量にも注目しなければなりませんが、ここでは計算量について考えてみます。
ある問題に対する「アルゴリズム」というのは、その問題のための有限回の基本演算（四則計算や比較演算、代入など）の一連の手続きのことです。問題のサイズ（問題の対象となるものの個数）を$N$とすると、それら全てにある演算を施す場合の計算量は$f(N)$と関数の形で表現されます。問題のサイズ$N$が大きくなるにつれて演算の数がどのように増えていくのかを分かりやすくするために関数$f(N)$のオーダー$O(f(N))$に注目します。
「オーダー」とは簡単に言うと、その関数の最高次の項のことですが、必ずしも整式で表現しなければならないわけではありません。例えば、$O(N^2)$、$O(2^N)$、$O(\log N)$、$O(N\log N)$などのように表現します。ここで$O$は「ランダウの記号」を表しています。
オーダーを可視化してみると以下のようになります。$N$が増えれば増えるほどオーダーが計算量に効いてくることが分かりますね。$O(\log N)$のグラフは他に比べてほとんど横ばいに見えますが、実際に$O(\log N)$のアルゴリズムは速いです（ユークリッドの互除法など）。
※アルゴリズムのオーダーの詳細については、大槻兼資さんがQiita上で公開している「計算量オーダーの求め方を総整理！ 〜 どこから log が出て来るか 〜」という記事が非常に参考になるかと思います。
問題のサイズ$N$に対して計算時間が$N$のべき乗で増える場合、その問題の計算量は多項式時間であると言います。もしくは、その問題は「クラスＰに属する」と言います。また、多項式時間で問題を解くことができるアルゴリズムを「多項式時間アルゴリズム」と呼びます。
※Ｐの文字は多項式を意味する “Polynomial” の頭文字から来ています。
巡回セールスマン問題を総当たりで解く際の計算量は$O(n!)$のオーダーになるため、上のグラフで言うと縦軸にほとんど張り付くレベルの絶望的な計算量に相当します。
巡回セールスマン問題は、多項式時間で解けるアルゴリズムが存在しない問題である「ＮＰ困難」と呼ばれるクラスに分類されています。実は、多くの組合せ最適化問題はＮＰ困難であることが知られています。そこで、このような最適化問題に対しては厳密解ではなく近似解を求めるアプローチが有効になります。
厳密解法と近似解法
一般に多項式時間アルゴリズムは「効率が良い」部類に属し、指数関数以上のオーダーで計算量が増加するアルゴリズムは「効率が悪い」と言えます。ユークリッドの互除法のようにすぐ終わってしまう巡回セールスマン問題のように、厳密な解を求めるには恐ろしく時間がかかってしまう問題もあるのです。
組み合わせ最適化問題に対する解法には「厳密解法」と「近似解法」の2種類があり、問題のオーダーに応じて現実的な計算時間で解決できる解法を選択しなければなりません。
「厳密解法」とは、探索を効率化しつつも、必ず大域的最適解を得ようとする手法であり、無駄な解の列挙を省きながら探索する「分枝限定法」や、問題を複数の部分問題に分割し、過去に得られた解の情報を利用しながら探索する「動的計画法」などがあります。
「近似解法」とは、最適解は諦める代わりに現実的な計算時間内で、ある程度良い近似解を得る手法であり、その時点で見つかっている最良の解に木（Tree）を付け足して探索する「貪欲法」や、既に得られている局所最適解のパラメータを修正しながら近傍を探索する「局所探索法」などがあります。
近似解と最適解の離れ具合を表す尺度として「近似比」というものが用いられます。
近似比：近似値を最適値で割った値
・最小化問題（目的が値を小さくする問題）では１以上
・最大化問題（目的が値を大きくする問題）では１以下
ここでは解に付随する数値をもとに最適解と（多数の）近似解を数値化して近似比というものを考えています。巡回セールスマン問題の場合はそれぞれの解が与える移動距離を解に付随する数値として扱えば良いでしょう。
近似比が１に近いほど最適値に近い近似値を与えるため、良い近似解であると言えます。最適解が分からない状態では近似比を算出することはできませんが、近似比が一定の値より悪くならないような近似解を求めるアルゴリズムの存在を理論的に証明できる場合もあります。
問題によっては最適解が一つだけであるという保証は全くありません。定義域全体で目的関数を見たときに、複数の極小な点が存在する場合があります。
そのうち最も値の小さいもの（あるいは大きいもの）を「大域的最適解」（global minimum）と呼び、それ以外の極小値を「局所最適解」（local minimum）と呼びます。
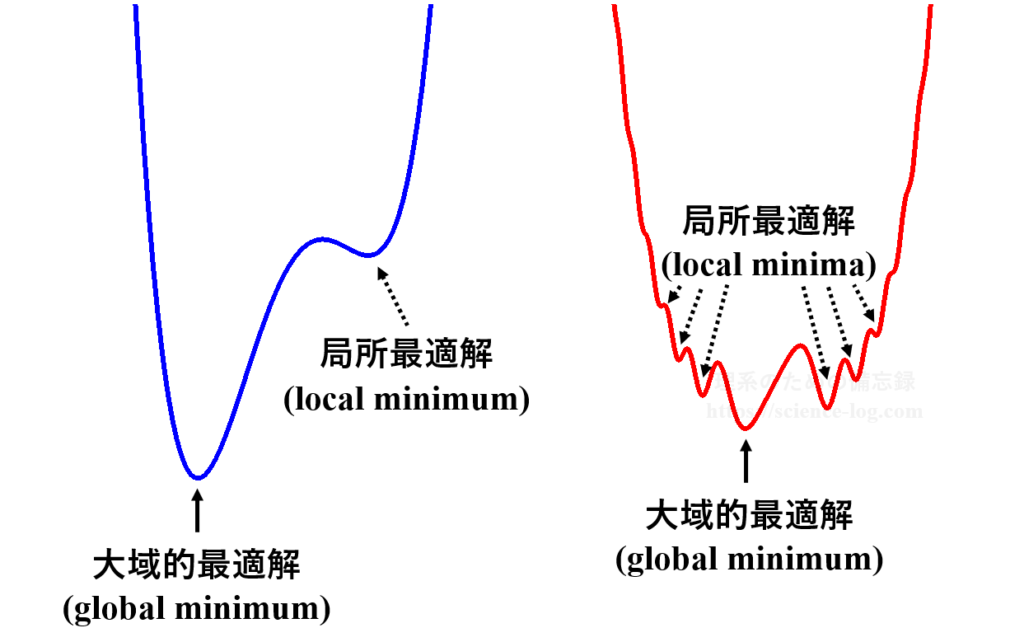
相手にしている目的関数によっては、大域的最適解以外にも多数の局所最適解が存在する場合があります。上の模式図は非常に単純な例ですが、左側の関数だと局所最適解の周辺を探すだけで大域的最適解が見つかりますが、右側のようなwell（井戸）の多い複雑な関数だと最初に局所最適解が見つかってしまい、大域的最適解を見逃してしまう可能性も出てきます。実際には２次元の関数ではなく遥かに複雑な多次元関数を対象にするので、大域的最適解の見落としは実用上シビアな問題です。
これを防ぐために様々なアルゴリズムが考案されています。詳しくは触れませんが、例えば「メタヒューリスティクス」と呼ばれる、より多くの計算資源を用いてより良い解を見つけ出すタイプの解法などが提案されています。この辺りの最適解の探索手法の開発は現在の情報科学のホットトピックでもあります。
上記の他にも様々な探索手法が存在します。アルゴリズムの詳細については該当するWikipediaのページや関連書籍･ウェブサイトを参考にしてください。
終わりに＆参考文献の紹介
ここまで、最適化問題のイロハのイの部分について解説してきました。
これまでに見てきたように、組み合わせ最適化の手法は組み合わせ論やグラフ理論などと密接に関わっており、対して連続最適化の手法を実装するには解析学の知識が必要となります。また、最適化問題を扱う上ではどちらのタイプの最適化問題にも共通して線形代数の知識が必須となります。
ちょっとした大型書店に行けば最適化問題に関する書籍が大量に置いてあります。その中に情報科学の顔をして数学や統計学の入門書が紛れ込んでいることに気が付くでしょう。データサイエンスには数学と統計学の知識が不可欠なのです。もし自身の数学力に不安があるのであれば、今のうちに一通りおさらいしておくことをお勧めします。もちろん、その場その都度で調べながら勉強して行っても良いと思いますが、数学の勉強は避けて通れない道です。
※言い換えれば、数学力が要求される情報科学の技能は誰でも身に付けられるものではありません。言ってしまえば特殊技能です。世の中に数学嫌いの人が多ければ多いほど、数学を使いこなせる人材の価値は高まります。数学教育は不要などと言い放って最近物議を醸したどこぞの金融担当大臣もいたようですが、個人の意見はともかく、日本の若者が数学に触れられる機会を構造的なレベルで除去してしまうのは愚かな施策と言わざるを得ません。
そして当然、最適化問題はプログラミングによって解くので、プログラミングの知識も必要となります。幸いなことに、最近になって経済産業省が「巣ごもりDXステップ講座情報ナビ」と題して、DXを推進するために情報科学に関する様々な教材を（今年限りという期間限定ですが）無償で公開してくれています。プログラミングの初歩だけでなく機械学習やAIの実装など発展的な内容まで網羅しており、情報科学の基礎知識が一通り学べる初学者向けの教材が揃っています。これは凄いことです。（学生の方は特に）この機を逃さずに、是非もう一段上のスキル獲得を目指してみてください！
「巣ごもりDXステップ講座情報ナビ」の知名度が低いようでは勿体ないと思い、勝手ながら紹介させて頂きました。
以下の書籍は数理最適化の世界を案内してくれる入門書です。
ただし、いずれの書籍もコードがどっさり掲載されているという訳ではなく、これらを読んだからと言って実際にプログラミングが上達するようなものではないので注意して下さい。最適化手法の仕組みを勉強する際にオススメの本です。
今後、この【最適化問題の基礎】シリーズは不定期で少しずつ更新していく予定です。次回は最も単純な連続最適化の手法の一つである「最急降下法」について具体的な例を交えながら解説します。