前回は最適化問題の基礎知識についてお話しました。今回は、最適化問題のうち、「連続最適化」の問題を解くために用いられる手法の一つである「最急降下法」について解説していきます。
連続最適化とは?
「連続最適化」とは簡単に言うと、連続的に定義された目的関数の値を最小化あるいは最大化する最適化問題の解法や、その考え方の枠組みのことを指しています。例えば、ある関数の極小値や極大値、またそれらを与える条件などを求めるときに連続最適化の手法が使われます。
連続最適化の具体例を見てみましょう。
ある点列データが与えられているとします。その散布図を以下に示します。
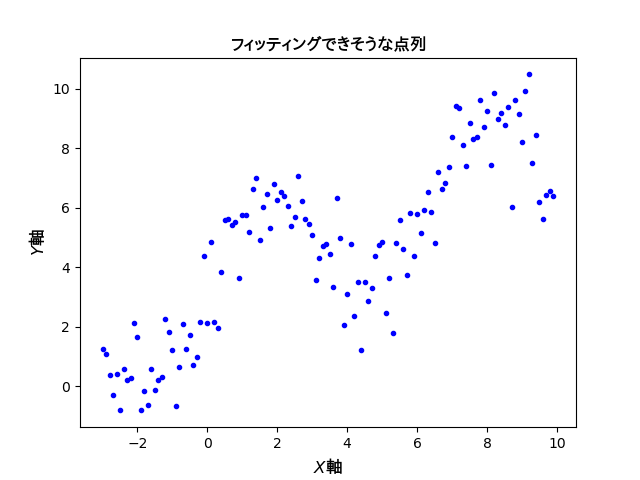
これらのデータ点をできるだけ精度よく再現する回帰曲線を得るために「最小二乗法」によるフィッティングを実行してみます。最小二乗法とは、元のデータセットと適当なモデル関数との誤差が最小となるようにモデル関数のパラメーターを決定する連続最適化の手法です。ここで言う誤差は、正確には「残差の平方和」などと呼ばれるもので評価され、これを最小化するように最適化を行います。
得られた結果を下に示します。
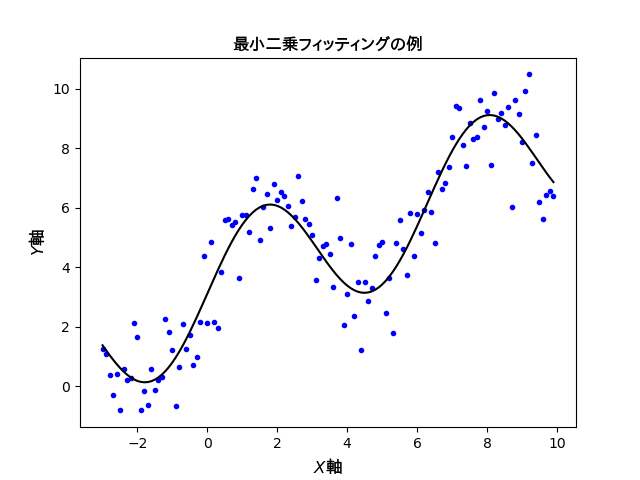
各データ点の$y$座標とフィッティング曲線が与える$y$座標の差を評価して、曲線のパラメータを決定しています。両者の$y$座標の差は曲線を微妙に動かせば連続的な値をとるので、連続最適化の手法が有効です。データ点自体は離散的なものですが、最適化の対象はあくまでも連続的な値や関数という訳です。
原理的には、どのような曲線および直線をパラメーターとしてフィッティングするかを決めて、誤差の二乗値をベクトル化して行列計算していけば上図のような曲線が得られます。上の例では1次関数と三角関数の足し合わせでフィッティング曲線を構成しています。
※参考:「最小二乗法のアルゴリズムを理解したのでメモ。そしてPythonで書いてみた。」by @ishizakiiii さん
※実際にコーディングする際は数値計算ライブラリなどに実装されているフィッティング用の関数を使うことが多いので、数学的な操作の中身はほとんどブラックボックス化されています。これは便利である反面、何をやってるかよく分からなくても何となく使えてしまうという怖さがあるとも言えます。
山を下るアルゴリズム
もっと直感的な例で連続最適化を考えてみましょう。
あなたはとある山の斜面にいます。最も効率的に下山するにはどのような方法で山を下れば良いでしょうか? もちろん現実的に考えれば、下るべき方向なんて景色を見ればすぐに分かりますが、目隠しされた状態でも下れる方法はないでしょうか?

プログラムには目がありません。当たり前のことですが、これは意外と大切なポイントです。プログラムには自分が今いる地点から見える景色が分からないのです。これは目隠しされて山の斜面にほっぽり出されている状況となんら変わりない訳です。
このような状態からでも、自分の周囲の地形を調べることによって山を下る方法(アルゴリズム)が存在します。その一つが「最急降下法」です。最急降下法とは、目的関数の勾配(1次微分)の情報を利用する「勾配法」と呼ばれる最適化手法の一つです。
最急降下法を使う前に、ちょっとした数学の準備をしておきます。
数値微分の方法
「最急降下法」とは、関数の勾配を調べて最も勾配の急な方向に下っていく方法です。最も勾配の急な方向に下っていけばいずれは勾配がゼロの点(地形で言えば「盆地」に相当する地点)が見つかるだろう、という仮定に基づく方法です。
最急降下法を利用するには、関数の勾配を調べる方法が必要となります。目的関数が陽な形($y=…$ の式で表される形のこと)で与えられているのであれば、全ての変数について解析的な導関数を求めることも不可能ではありません。ですが、いちいち手作業で解析的な導関数を求めるのは汎用的な方法ではありません。そこで関数を数値的に微分する方法が活躍します(これを「数値微分」と言います)。
まず微分について復習しておきましょう。
微分(導関数)の定義は以下のようなものでした。$$\displaystyle f^{\prime}(x)\equiv \lim_{h \to 0}\dfrac{f(x+h)-f(x)}{h}$$※「$\equiv$」という記号は「同等のものである」という意味です。
導関数は$$\displaystyle f^{\prime}(x)\equiv\dfrac{\mathrm{d}f(x)}{\mathrm{d}x}\equiv\nabla f(x)$$という文字式でも表現されます。1変数関数の場合はこのような書き方でも問題ありませんが、多変数関数の場合は以下のように変数を列ベクトルにまとめて書き下す方法がラクです。
※「$\nabla$」は微分を表す記号で「ナブラ」と読みます。
目的関数$f$が$n$個の変数$x_1, x_2, \cdots ,x_n$で定義される$n$変数関数の場合、変数を要素とする$n$行の列ベクトル$$\mathbf{x} = \left[\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right]$$に対して、目的関数$f$の導関数は$$\nabla f(\mathbf{x})=\left[\begin{array}{c} \dfrac{\partial f(\mathbf{x})}{\partial x_1} \\ \dfrac{\partial f(\mathbf{x})}{\partial x_2} \\ \vdots \\ \dfrac{\partial f(\mathbf{x})}{\partial x_n} \end{array}\right]$$と定義されます。行列を代入しているので、返ってくるのも行列(この場合は特に列ベクトル)になっています。ここで、$\nabla$が$n$個の変数$x_1, x_2, \cdots ,x_n$のすべてで微分する操作に対応する「演算子」になっていることを確認しておきましょう。
※ここで「$\partial$」は偏微分の記号で「関数をある1種類の変数について微分していますよ」という意味の記号です。多変数関数に対してしか使いません。偏微分について、詳しくは解析学の参考書を参照してください。
世の中に出回っている多くの情報科学の参考書にはベクトルや行列を使った表現が満載です。早いうちに行列表現に慣れておきましょう。
数値微分には主に前方差分、後方差分、中心差分の3種類があります。それぞれ定義式は以下のようになります。
-
- 前方差分:$f^{\prime}\left(x\right) \approx \dfrac{f\left(x+\delta\right)-f\left(x\right)}{\delta}$
($x$とその前方の点 $x+\delta$ との差分)
- 後方差分:$f^{\prime}\left(x\right) \approx \dfrac{f\left(x\right)-f\left(x-\delta\right)}{\delta}$
($x$とその後方の点 $x-\delta$ との差分)
- 中心差分:$f^{\prime}\left(x\right) \approx \dfrac{f\left(x+\delta\right)-f\left(x-\delta\right)}{2\delta}$
($x$を中心とする前後の点 $x+\delta$ と $x-\delta$ との差分)
- 前方差分:$f^{\prime}\left(x\right) \approx \dfrac{f\left(x+\delta\right)-f\left(x\right)}{\delta}$
※「$\approx$」という記号は「大体同じ」という意味です。
プログラムの中では$\delta$を$0.000001$といった非常に小さい値として定義します。これによって任意の関数$f(x)$について数値微分が可能となります。
【余談】数値微分の誤差について
ところで、これら3種類の差分のうち、最も精度よく導関数を表現している式はどれだか分かりますか? これを調べるために$f(x)$のテイラー展開を考えてみます。
$f(x+\delta)$を3次の項まで展開すると$$\small f(x+\delta)=f(x)+\delta f^{\prime}(x)+\dfrac{\delta^2}{2!}f^{\prime\prime}(x)+\dfrac{\delta^3}{3!}f^{\prime\prime\prime}(x)+O(\delta^4)$$となるので、$$\small\begin{aligned}
\dfrac{f(x+\delta)-f(x)}{\delta}&=f^{\prime}(x)+\dfrac{\delta}{2!}f^{\prime\prime}(x)+\dfrac{\delta^2}{3!}f^{\prime\prime\prime}(x)+O(\delta^3)\\
&=f^{\prime}(x)+\color{red}{O(\delta)}
\end{aligned}$$を得ます。これは前方差分の誤差が$\delta$の1次のオーダーで現れるということを意味します。
※「$O$」は「ランダウの記号」で「スモールオー」などと読まれます。この式は、$f^{\prime}(x)$が導関数の真の値を与えるならば$f^{\prime}(x)$と$\dfrac{f(x+\delta)-f(x)}{\delta}$の差は少なくとも$\delta$の1次以上の式で与えられる、ということを意味しています。
同様に$f(x-\delta)$を3次の項まで展開すると$$\small f(x-\delta)=f(x)-\delta f^{\prime}(x)+\dfrac{\delta^2}{2!}f^{\prime\prime}(x)-\dfrac{\delta^3}{3!}f^{\prime\prime\prime}(x)+O(\delta^4)$$となるので、$$\small\begin{aligned}
\dfrac{f(x)-f(x-\delta)}{\delta}&=f^{\prime}(x)-\dfrac{\delta}{2!}f^{\prime\prime}(x)+\dfrac{\delta^2}{3!}f^{\prime\prime\prime}(x)-O(\delta^3)\\
&=f^{\prime}(x)+\color{red}{O(\delta)}
\end{aligned}$$を得ます。後方差分も誤差が$\delta$の1次のオーダーになることが分かります。
ここで、$$\small f(x+\delta)=f(x)+\delta f^{\prime}(x)+\dfrac{\delta^2}{2!}f^{\prime\prime}(x)+\dfrac{\delta^3}{3!}f^{\prime\prime\prime}(x)+O(\delta^4)$$と$$\small f(x-\delta)=f(x)-\delta f^{\prime}(x)+\dfrac{\delta^2}{2!}f^{\prime\prime}(x)-\dfrac{\delta^3}{3!}f^{\prime\prime\prime}(x)+O(\delta^4)$$の差分は$$\small f(x+\delta)-f(x-\delta)=2\delta f^{\prime}(x)+\frac{2\delta^3}{3!}f^{\prime\prime\prime}(x)+O(\delta^4)$$となるので、$$\small\begin{align}\frac{f(x+\delta)-f(x-\delta)}{2\delta}&=f^{\prime}(x)+\frac{\delta^{2}}{3!}f^{\prime\prime\prime}(x)+O\left(\delta^{3}\right)\\&=f^{\prime}(x)+O\left(\delta^{2}\right)\end{align}$$であり、$$\small f^{\prime}(x)=\frac{f(x+\delta)-f(x-\delta)}{2\delta}+\color{red}{O\left(\delta^{2}\right)}$$と中心差分の誤差は$\delta$の2次のオーダーに抑えられることが分かります。
いま、$\delta$は微小量なのでオーダーが大きいほど小さい値をとります。したがって上記3種類のうち、最も高い精度の導関数を与えるのは中心差分と結論できます。
実際にプログラムで確認してみましょう。以下は$x$の微小変化量$\delta$を$$\delta =\text{1e}-4 \ (=0.0001)$$として $y=\sin x$ を $x=1.0$ の点で数値微分するコードです。
import math
def f(x):
return math.sin(x)
def fx_FW(x):
d = 1e-4
return (f(x)-f(x-d))/(d)
def fx_BW(x):
d = 1e-4
return (f(x+d)-f(x))/(d)
def fx_CT(x):
d = 1e-4
return (f(x+d)-f(x-d))/(2*d)
x = 1.0
print("FW =",fx_FW(x),abs((fx_FW(x)-math.cos(x))/math.cos(x)))
print("BW =",fx_BW(x),abs((fx_BW(x)-math.cos(x))/math.cos(x)))
print("CT =",fx_CT(x),abs((fx_CT(x)-math.cos(x))/math.cos(x)))
print("cos =",math.cos(x))
これを実行すると次の結果を得ます。
FW = 0.5403443785167994 7.786871942371074e-05 BW = 0.5402602314186211 7.78720524818856e-05 CT = 0.5403023049677103 1.666529087425379e-09 cos = 0.5403023058681398
FW、BW、CTはそれぞれ前方差分、後方差分、中心差分に対応しており、右側の数値は導関数の厳密値($\cos 1$)との相対誤差です。実際に、前方差分と後方差分は相対誤差が 7.787…e-05 と$\delta$の1次のオーダーになっており、中心差分では 1.666…e-09 と$\delta$の2次のオーダーになっていることが分かります。
なお、誤差の程度はその点における目的関数の曲率(変化率)にも依存します。例えば、$x=0.0$ 近傍では $y=\sin x$ の曲率がゼロ、つまりほぼ直線と見なせるので、いずれの差分でも誤差にほとんど違いは出ません。確かめてみましょう。
※$y=\sin x$ の曲率は $\dfrac{\sin x}{(1+\cos x)^{3/2}}$ の絶対値で与えられます。詳細は「曲率と曲率半径」のページを参考にして下さい。
最急降下法で山を下る!
それではいよいよ最急降下法で山を下ってみましょう。
最急降下法のアルゴリズムは次の通りです。
最急降下法
STEP 0: 初期値$\mathbf{x}^{(0)}$を決める($i=0$)
STEP 1: $\nabla f\left(\mathbf{x}^{(i)}\right)< \epsilon$ ならば終了
そうでなければ $\mathbf{d}^{(i)}=\nabla f\left(\mathbf{x}^{(i)}\right)$ と置く
STEP 2: ステップ幅を$\alpha \,(>0)$とする
$\mathbf{x}^{(i+1)} := \mathbf{x}^{(i)}-\alpha \mathbf{d}^{(i)}$ と置く
$i := i + 1$ と置いてSTEP 1 に戻る
これだけを見てもよく分からないと思うので、1変数の関数 $f(x)=x^2$ について最急降下法を用いたときの模式図で説明します。
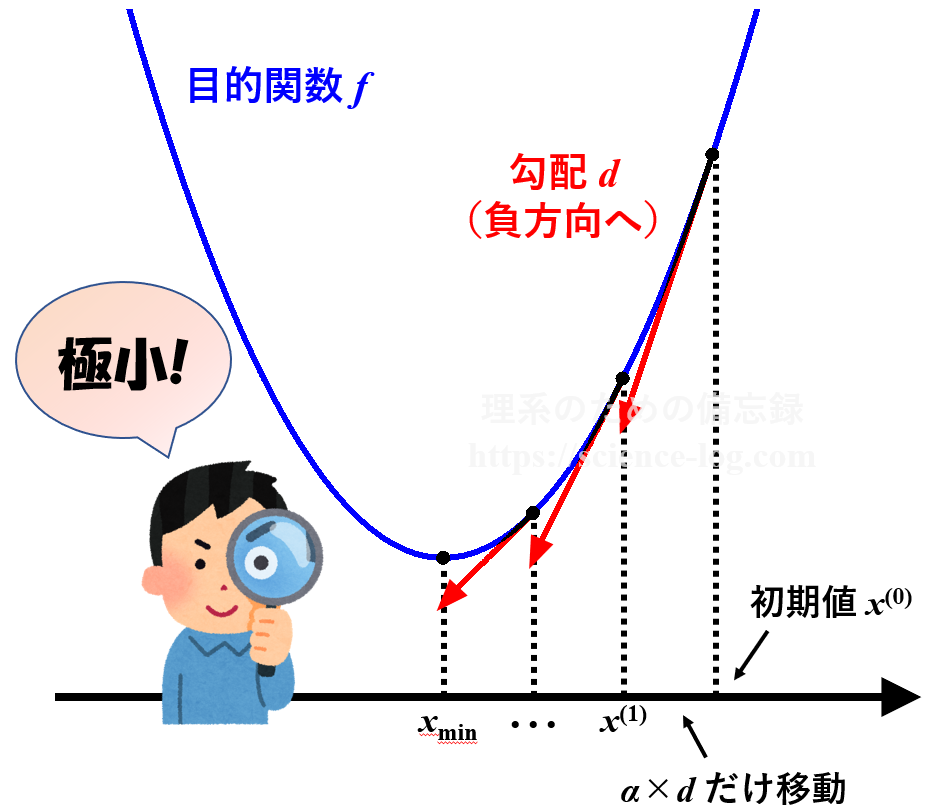
まず初期値$x^{(0)}$を決めます。例えば $x^{(0)}=3.0$ とすると、その点における勾配$d$は導関数 $f'(x)=2x$ から $d=6.0$ と求められます。ステップ幅$\alpha$を $\alpha=0.1$ とすると、次の点$x^{(1)}$は$$\begin{align} x^{(1)} &=x^{(0)}-\alpha d \\ &=3.0-0.1 \times 6.0 \\ &=2.4 \end{align}$$と求められます。$x^{(1)}=2.4$ における勾配は $f'(2.4)=4.8$ であり$0$には程遠いので、再び上と同じ操作を実行します。
これを何度も繰り返していくうちに、上手くいけば勾配$d^{(i)}$はだんだんゼロに近付いていき、座標$x^{(i)}$も極小点である $x=0$ に近付いていきます。そこで、事前に決めておいたある一定の値$\epsilon$を勾配の値が下回った時点で、その点が極小点であると見なして操作を終了します。
このような一連の流れで山を下っていく方法が「最急降下法」です。もし逆に山の頂点を見つけたい場合は「STEP 2」の$\alpha$の符号を逆にすれば山を登っていきます。
※ステップ幅$\alpha$は、機械学習では「学習率」と呼ばれる値に相当します。
2次元の場合を考えてみます。$$f(x_1,x_2) = 2\cos(2^{x_1}-x_2^2+1)+e^{(x_1^2+x_2^2)/6}$$という式で表される2変数関数を例に考えてみましょう。
下の図は初期値 $(x_1,x_2) =(-0.5,\,1.0)$ から $\alpha=0.1$ として最急降下法によって$f(x_1,x_2)$を最小化したときの軌跡をプロットしたものです(横軸が$x_1$軸、縦軸が$x_2$軸)。赤色の濃い部分が「標高の高い所」、青色の濃い部分が「標高の低い所」という風にイメージして下さい。
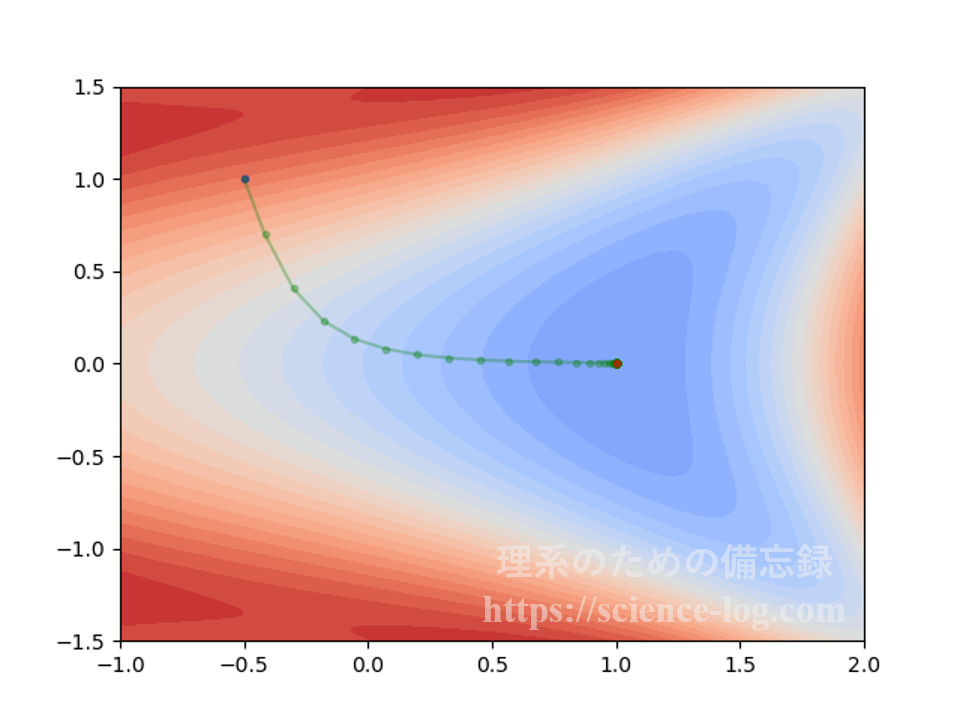
これを3次元表示すると下図のようになります。立体的に見た方が、ちゃんと山下りしているのが分かりやすいかもしれません。
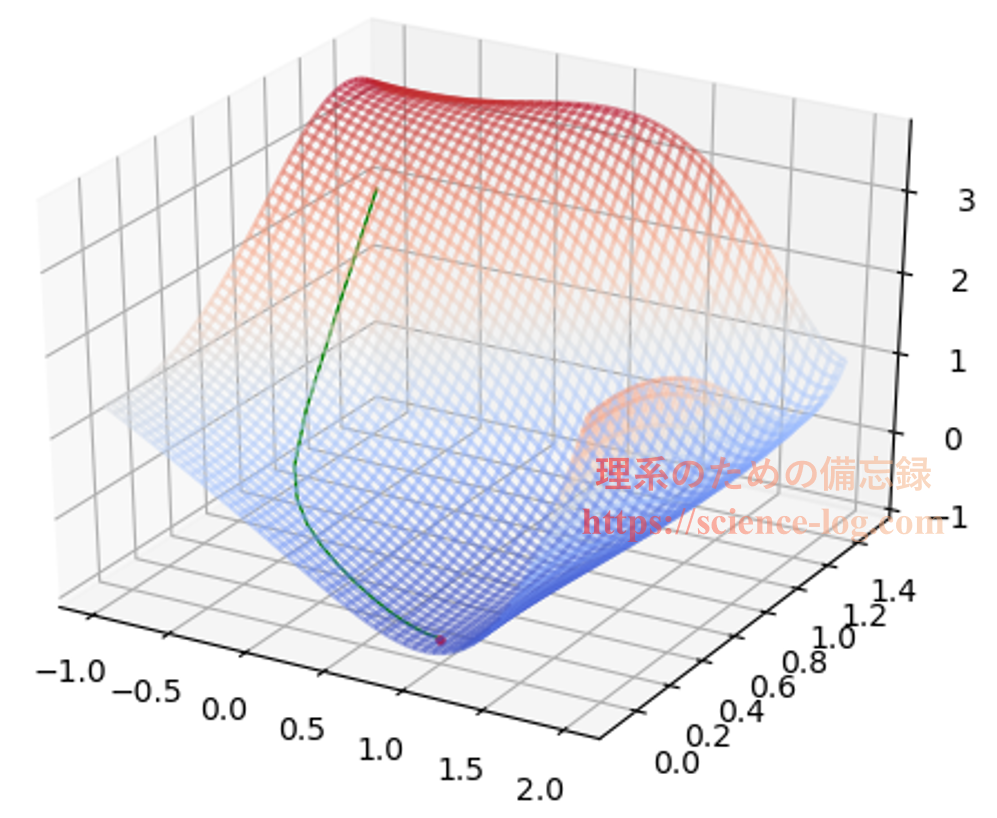
上図で表示している範囲における関数$f(x_1,x_2)$の極小点は$x_2$軸上に存在しており、$$x_1 ≈ 0.99937896553746259…$$となる点です。上図で終点になっている赤色の点はこの極小点に対応しています。
関数$f(x_1,x_2)$の偏導関数はそれぞれ$$\small \begin{align} & \dfrac{\partial}{\partial x_1}f(x_1,x_2) \\ =&\, -2^{x_1+1} \log 2 \cdot \sin \left(2^{x_1}-x_2^{2}+1\right)+\dfrac{1}{3} x_1 e^{1 / 6\left(x_1^{2}+x_2^{2}\right)} \end{align}$$および$$\small \begin{align} & \dfrac{\partial}{\partial x_2}f(x_1,x_2) \\ =&\, 4 x_2 \sin \left(2^{x_1}-x_2^{2}+1\right)+\dfrac{1}{3} x_2 e^{1 / 6\left(x_1^{2}+x_2^{2}\right)} \end{align}$$で与えられます。数値微分とのズレを比較検証してみるのも面白いかもしれませんね。
手元でプログラムを動かして、実際にどのような挙動をしているのかを確認してみて下さい。以下に必要最低限のサンプルコードだけ置いておきます。コーディングには色々なやり方があり、これが正解、というものでは全くありません。初期値やステップ幅などを色々いじって遊んでみて下さい。
import math
def f(x, y):
return 2*math.cos(2**x+1-y**2)+math.e**((x**2+y**2)/6)
def fx(x, y):
h = 1e-7
return (f(x+h, y)-f(x-h, y))/(2*h)
def fy(x, y):
h = 1e-7
return (f(x, y+h)-f(x, y-h))/(2*h)
xc1 = -0.5; yc1 = 1.0 # 初期値
stepsize = 0.1 # ステップ幅
maxtimes = 10000 # 最大試行回数
times = maxtimes # 試行回数カウント用変数
# steepest descent method 最急降下法
for i in range(1, maxtimes): # 最大試行回数に達するまで繰り返す
diffx1 = fx(xc1, yc1); diffy1 = fy(xc1, yc1); backward = f(xc1,yc1)
if math.sqrt(diffx1 ** 2 + diffy1 ** 2) < 1e-7: # 終了条件
times = i
break
else:
xc2 = xc1 - stepsize * diffx1 # 次のx座標を生成
yc2 = yc1 - stepsize * diffy1 # 次のy座標を生成
forward = f(xc2,yc2) # 次の座標での値
if forward < backward: # もし関数の値が小さくなったら
xc1 = xc2; yc1 = yc2 # 座標の更新
backward = forward
else: # もし関数の値が小さくならなかったら
stepsize = stepsize * 0.5 # ステップ幅を減衰(オプション)
# 試行回数
print("done! ( i =", times, ")")
# 極小点の座標
print("(", xc1, ",", yc1,")")
# 極小点での値と勾配の大きさ
print("z =", f(xc1, yc1), ", |d| =", math.sqrt(diffx1 ** 2 + diffy1 ** 2))
※ステップ幅が一定だと極小点付近で振動してしまうので、座標更新後に値が大きくなってしまった場合にステップ幅を半分にする操作を挟んでいます。この辺りの最適な数値は初期値や目的関数の形状にもよるので、適宜お好みでアレンジして下さい。
※mathモジュールをインポートする代わりにPythonの数値計算ライブラリ「Numpy」をインポートしてもよいでしょう。導入していない方はインストールしておくことをお勧めします。導入方法については色々なサイトで解説されていますので、調べてみて下さい。必要に応じて「Pythonプログラミングtips集」のページも参考にして下さい。
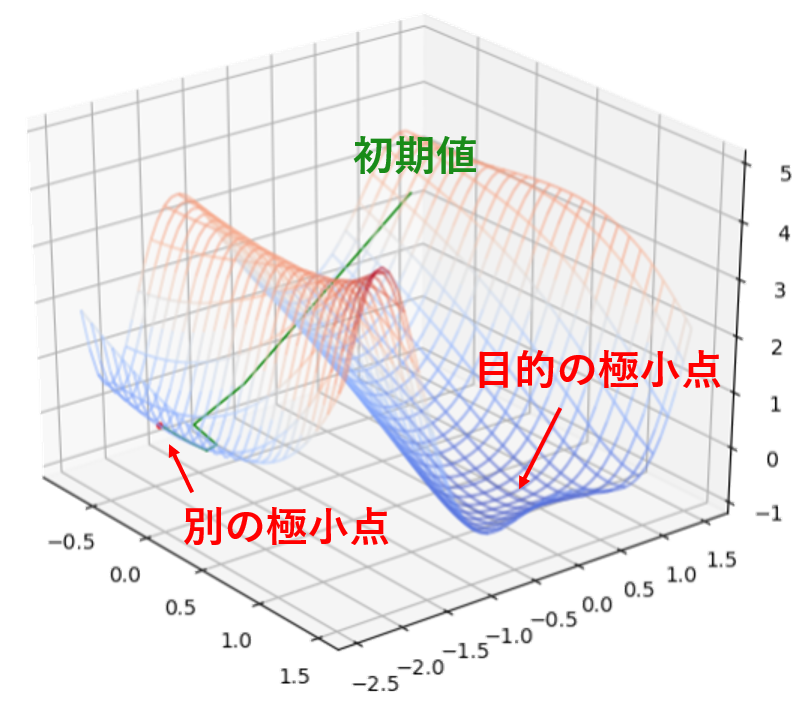
最急降下法は簡単に実装できる手法ですが、万能という訳ではありません。例えば先ほどの2変数関数の例で、ステップ幅$\alpha$を$0.1$ではなく$1.0$にすると初期値 $(x_1,x_2) =(-0.5,\,1.0)$ から一気に隣の山を飛び越えて別の極小点に到達してしまいます。
また、ステップ幅$\alpha$が一定のままだと極小点付近で延々と「振動」してしまい、正確な極小点がいつまでたっても求められない場合もあります。例えば、初期値を $(x_1,x_2) =(0.5,\,0.5)$ として $\alpha=0.53$ で一定にすると以下に示すように振動して極小点に至りません(下図は$2000$回の座標更新が終了した時点の様子)。
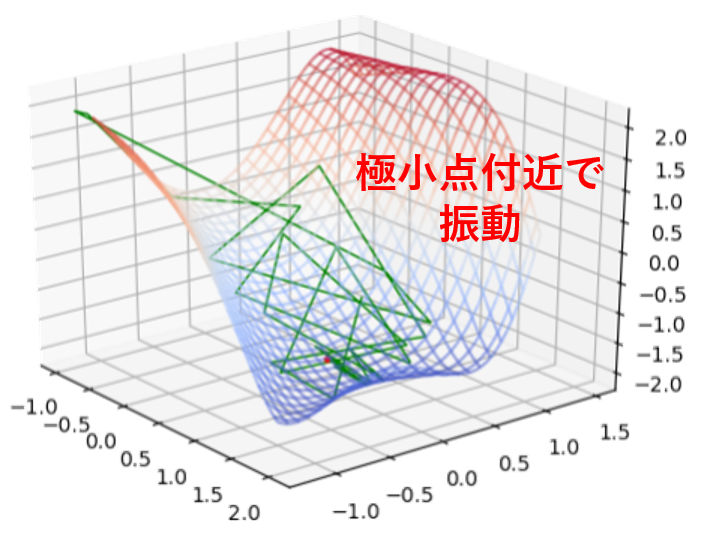
このようなケースを防止するため、座標と同時に$\alpha$の値も一緒に更新するアルゴリズムが有効です。例えば、上のサンプルコードでは値の大きな点に移動してしまったらステップ幅を半分にする操作をしています(ただしこれはちょっと雑な方法です)。
よく用いられる理論的な制約としては「ウルフの条件」(Wolfe conditions)や「アルミホの条件」(Armijo rule)などがあります。詳しくは「Backtrackingアルゴリズム」などで調べてみて下さい。気が向けば別途、解説記事を公開します…。
※出力結果をグラフで表示したい場合は「【Python】matplotlibでグラフを作成する方法【総まとめ】」の記事を参考にして下さい。思い通りのグラフが表示できると楽しいですよ!
まとめ
最急降下法は目的関数の勾配(1次微分)の情報を使って最適化するアルゴリズムで、「勾配法」と呼ばれる最適化手法の代表的なものです。単純な手法なので実装は容易ですが、実用する際は気を付けなければいけない点も幾つかあることを紹介しました。最急降下法は連続最適化の入門としてちょうどよい題材なので、取り扱っている書籍やウェブサイト、動画などが山のように出回っています。色々な人の解説を読んで(聞いて)原理をよく理解しておきましょう。
山下りの方法は最急降下法の他にも色々知られています。次回は、目的関数の勾配の勾配(2次微分)の情報を使って最適化する「ニュートン法」という手法について解説します。
