【最適化問題の基礎】準ニュートン法とセカント条件

前回解説した「ニュートン法」の弱点と、その改良版である「準ニュートン法」について解説します。準ニュートン法の実装例と結果についても掲載しています。

---

 

 ニュートン法の弱点

前回までの記事で見てきたように、ニュートン法は極めて速い収束速度を誇る最適化手法です。しかしニュートン法にはいくつかの弱点が存在します。

ニュートン法では、目的関数の2次微分（ヘッセ行列）によって最適化が行われており、目的関数の1次微分、すなわち勾配がゼロになる点に向かって座標を更新していきます。つまり、ニュートン法で最終的に辿り着く点は「勾配がゼロである点」であって、必ずしも極小点とは限りません。したがって、ニュートン法では必ずしも目的関数の局所最適解が求められる訳ではないことに注意する必要があります。

また、ニュートン法ではヘッセ行列の逆行列を用いて探索方向を定めますが、ヘッセ行列の(半)正定値性や正則性は常に保証されている訳ではないため、ニュートン法が破綻する（収束しない）場合があります。

こうした問題点を改善するために考え出されたのが「準ニュートン法」です。

 

 準ニュートン法のコンセプト

「準ニュートン法」(quasi-Newton method) ではヘッセ行列をそのまま使うのではなく、ヘッセ行列を近似した正定値行列を用いて降下方向（ニュートン方向）を決定します。ニュートン法ではヘッセ行列の逆行列を求める必要がありますが、ヘッセ行列の中身によっては上手く最適化できない場合が多々あります。そこで、この「ヘッセ行列の逆行列」を近似できるような「都合の良い」行列を使って最適化できないだろうか？というのが準ニュートン法のモチベーションになっています。

ニュートン法では、

1. 1. ヘッセ行列 ${\mathrm{\nabla }}^{2}f(\mathit{x})$ を計算する
   2. 方程式 ${\mathrm{\nabla }}^{2}f(\mathit{x})\mathrm{\Delta }\mathit{x}=-\mathrm{\nabla }f(\mathit{x})$ から降下方向$\mathrm{\Delta }\mathit{x}$を求める
   3. 座標更新＆収束判定

という手順で座標を更新していきますが、準ニュートン法ではヘッセ行列を使わず、$$\mathit{B}\mathrm{\Delta }\mathit{x}=-\mathrm{\nabla }f(\mathit{x})$$という方程式を満たすような「計算しやすい」行列$\mathit{B}$を新しく作って降下方向を決定します。

準ニュートン法の手順は以下のようになります。

1. 1. 方程式 $\mathit{B}\mathrm{\Delta }\mathit{x}=-\mathrm{\nabla }f(\mathit{x})$ から降下方向$\mathrm{\Delta }\mathit{x}$を求める
   2. 座標更新＆収束判定
   3. 行列$\mathit{B}$を更新する
      （$\mathit{B}$は特に理由がなければ最初は単位行列$\mathit{I}$とする）

この「ヘッセ行列もどき」は iterative に更新されるので、多くの教科書で「${\mathit{B}}_k$」のように添え字付きで表記されています。もしくは近似ヘッセ行列${\mathit{B}}_k$の逆行列を ${\mathit{H}}_k={\mathit{B}}_k^{-1}$ と表記することも多いです（$\mathit{H}$はヘッセ行列のことではないので注意）。

行列$\mathit{B}$あるいは$\mathit{H}$を考えることには、

• • ニュートン法と同じ方程式で降下方向を定めることにより優れた収束速度を保つ
  • 正定値行列になるよう加工して最適化が破綻しないようにできる

というメリットがあります。

---

※参考：“Variable Metric Method for Minimization” by William C. Davidon（原本はこちら）

※準ニュートン法がダヴィドンによって考案されたのは、数学者コーシーが1847年に最急降下法を定式化してからおよそ100年後のことでした。そう考えると2050年頃には別の画期的な最適化手法が編み出されているかもしれませんね！

 

 セカント条件とは？

準ニュートン法で利用する行列$\mathit{B}$と、その逆行列$\mathit{H}$には「セカント条件」と呼ばれる制約が要請されます。

近似ヘッセ行列$\mathit{B}$は$$\mathrm{\nabla }f({\mathit{x}}_k+\mathrm{\Delta }\mathit{x})=\mathrm{\nabla }f({\mathit{x}}_k)+\mathit{B}\mathrm{\Delta }\mathit{x}$$という関係式を満たすように構成されます。これを「セカント方程式」と呼びます。セカント方程式は$${\mathit{B}}_k({\mathit{x}}_k-{\mathit{x}}_{k+1})=\mathrm{\nabla }f({\mathit{x}}_{k+1})-\mathrm{\nabla }f({\mathit{x}}_k)$$と書き直せるので、$${\mathit{B}}_{k+1}{\mathit{s}}_k={\mathit{y}}_k$$または$${\mathit{H}}_{k+1}{\mathit{y}}_k={\mathit{s}}_k$$と表現されます。これらの制約のことを「セカント条件」と呼んでいます。さらに、このような正定値行列$\mathit{B}$が存在するためには、${\mathit{s}}_k\ne \mathbf{0}$ において$${\mathit{s}}_k^{\mathrm{\top }}{\mathit{y}}_k>0$$を満たすことが要請されます。これはウルフ条件を満たすように${\mathit{s}}_k$を定めることで満足されます。

以上の諸々の制約をクリアして行列$\mathit{B}$を更新する手法が幾つか提案されています。

 

 近似行列の更新方法

セカント条件を満たすような行列は無数に存在するので、その定義や更新方法にはバリエーションがあります。ここでは代表的な更新方法である「DFP公式」と「BFGS公式」と「SR1公式」について紹介します。ベクトルの乗算の順序が書籍等によって異なる場合がありますが中身は同じものです。

（※以下の式中にある$\mathit{I}$は単位行列です）

DFP公式：$$\begin{array}{l}{\mathit{B}}_{k+1}=(\mathit{I}-{\displaystyle \frac{{\mathit{y}}_k{\mathit{s}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^{\mathrm{\top }}{\mathit{s}}_k}}){\mathit{B}}_k(\mathit{I}-{\displaystyle \frac{{\mathit{s}}_k{\mathit{y}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^{\mathrm{\top }}{\mathit{s}}_k}})+{\displaystyle \frac{{\mathit{y}}_k{\mathit{y}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^{\mathrm{\top }}{\mathit{s}}_k}}\\ {\mathit{H}}_{k+1}={\mathit{H}}_k+{\displaystyle \frac{{\mathit{s}}_k{\mathit{s}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^T{\mathit{s}}_k}}-{\displaystyle \frac{{\mathit{H}}_k{\mathit{y}}_k{\mathit{y}}_k^{\mathrm{\top }}{\mathit{H}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^{\mathrm{\top }}{\mathit{H}}_k{\mathit{y}}_k}}\end{array}$$

BFGS公式：$$\begin{array}{l}{\mathit{B}}_{k+1}={\mathit{B}}_k+{\displaystyle \frac{{\mathit{y}}_k{\mathit{y}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^T{\mathit{s}}_k}}-{\displaystyle \frac{{\mathit{B}}_k{\mathit{s}}_k{\left({\mathit{B}}_k{\mathit{s}}_k\right)}^{\mathrm{\top }}}{{\mathit{s}}_k^{\mathrm{\top }}{\mathit{B}}_k{\mathit{s}}_k}}\\ {\mathit{H}}_{k+1}={(\mathit{I}-{\displaystyle \frac{{\mathit{y}}_k{\mathit{s}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^{\mathrm{\top }}{\mathit{s}}_k}})}^{\mathrm{\top }}{\mathit{H}}_k(\mathit{I}-{\displaystyle \frac{{\mathit{y}}_k{\mathit{s}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^{\mathrm{\top }}{\mathit{s}}_k}})+{\displaystyle \frac{{\mathit{s}}_k{\mathit{s}}_k^{\mathrm{\top }}}{{\mathit{y}}_k^{\mathrm{\top }}{\mathit{s}}_k}}\end{array}$$

BFGS公式は準ニュートン法において最も頻繁に用いられている更新式です。式の形を見ても分かる通り、DFP公式とBFGS公式には密接な関係があります。ここでは導出や収束性に関する数学的な証明には深く立ち入りませんので、詳細については「機械学習のための連続最適化」などの専門書に当たって下さい。この書籍では数式を用いて詳解されているので、原理をしっかり理解したい人にオススメです。

この他に利用されることのある更新則としては「SR1公式」が挙げられます。

SR1公式：$$\begin{array}{l}{\mathit{B}}_{k+1}={\mathit{B}}_k+{\displaystyle \frac{({\mathit{y}}_k-{\mathit{B}}_k{\mathit{s}}_k){({\mathit{y}}_k-{\mathit{B}}_k{\mathit{s}}_k)}^{\mathrm{\top }}}{{({\mathit{y}}_k-{\mathit{B}}_k{\mathit{s}}_k)}^{\mathrm{\top }}{\mathit{s}}_k}}\\ {\mathit{H}}_{k+1}={\mathit{H}}_k+{\displaystyle \frac{({\mathit{s}}_k-{\mathit{H}}_k{\mathit{y}}_k){({\mathit{s}}_k-{\mathit{H}}_k{\mathit{y}}_k)}^{\mathrm{\top }}}{{({\mathit{s}}_k-{\mathit{H}}_k{\mathit{y}}_k)}^{\mathrm{\top }}{\mathit{y}}_k}}\end{array}$$

SR1公式は疎性のある最適化問題などに対して有効な手法であるとされており、BFGS公式よりも良いパフォーマンスを示すケースも報告されています。ただしSR1公式では、近似ヘッセ行列$\mathit{B}$はセカント条件を満たしますが、正定値性は保証されていません。

---

準ニュートン法では座標更新の際に過去のステップで得た近似ヘッセ行列を使うため、$n\times n$ の行列をメモリに保存する必要があります。次元数が大きくなるにつれてメモリ使用量が増大してしまうのを防ぐため、大規模な計算の際にメモリ使用量を節約する手法として「記憶制限付き準ニュートン法」が利用されています。これは「L-BFGS法」などとして実用されています。L-BFGS法では、過去に得られている幾つかの近似ヘッセ行列の逆行列をもとに新たな行列${\mathit{H}}_k$を生成します。ここで、行列を陽に保持するのではなくベクトルの内積計算の結果として保持することで、メモリ使用量を大幅に削減できるようです。

※同様にSR1法についても「記憶制限付きSR1法」(L-SR1法) というものが提案されており、ニューラルネットワークの学習における高次元最適化でL-BFGS法を凌駕する可能性を主張する論文もあるようです。この辺りの事情について管理人はあまり詳しくないので、最先端の2次最適化手法について興味がある方は表現学習分野などの学術論文を参照して下さい･･･。

 

 準ニュートン法の実装例

BFGS法を用いた準ニュートン法のアルゴリズムは次のようになります。

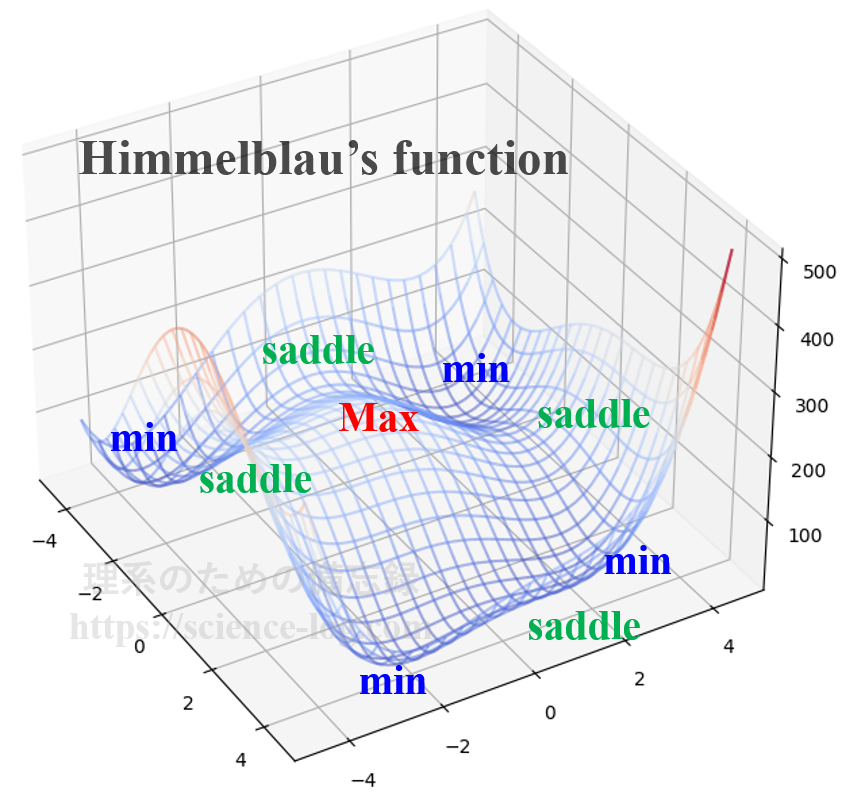
これを実装して極小点を探索してみましょう。ここでは、前回の記事でも取り上げたHimmelblau’s function（ヒンメルブラウの関数）という2変数関数に対して、BFGS法を用いた準ニュートン法により最適化してみることにします。ヒンメルブラウの関数は$$f(x,y)=(x^2+y-11{)}^2+(x+y^2–7{)}^2$$という方程式で与えられ、曲面の立体的な形状は下図のようになっています。

以下にサンプルコードを示します。関数の引数にベクトルを渡すようにすれば、もっとシンプルに書けると思います。

import numpy as np

def f(x, y):
    return (x**2 + y -11)**2 + (x + y**2 - 7)**2

def fx(x, y):
    h = 0.0000001
    return (f(x+h, y)-f(x-h, y))/(2*h)

def fy(x, y):
    h = 0.0000001
    return (f(x, y+h)-f(x, y-h))/(2*h)


# input section
X = [3.0, 0.5]   # 初期座標をベクトルに格納
rho = 0.9        # 直線探索のパラメータ
c = 0.4          # 直線探索のパラメータ
B = np.array([[1.0, 0.0], [0.0, 1.0]])  # 近似ヘシアンBは単位行列として始める
grad = [fx(X[0], X[1]), fy(X[0], X[1])] # 勾配をベクトルに格納
maxtimes = 10000
times = maxtimes

for i in range(1, maxtimes):
    diffx1 = fx(X[0], X[1]); diffy1 = fy(X[0], X[1])
    if np.linalg.norm(grad) < 1e-7:
        times = i
        break
    else:
        # Armijo条件による直線探索
        k = 0
        alpha = 1.0
        f_init = f(X[0], X[1])
        d = - np.dot(np.linalg.inv(B), [diffx1, diffy1]) # セカント条件により定まる探索方向
        dot_tmp = c * np.dot(grad, d)
        X_tmp = X + alpha * d   # 更新先の座標(仮)
        while f(X_tmp[0], X_tmp[1]) > f_init + alpha * dot_tmp:
            alpha *= rho            # alpha を更新
            X_tmp = X + alpha * d   # 更新先の座標(仮) X_tmp を更新
        X += alpha * d              # 座標更新

        # 近似ヘッセ行列の更新
        old_grad = grad                                    # 前の勾配ベクトルの保存
        grad = np.array([fx(X[0], X[1]), fy(X[0], X[1])])  # 勾配ベクトルを更新
        s = (alpha * d).reshape([-1,1])                    # 座標の変化量 (reshapeメソッドで列ベクトル化)
        y = (grad - old_grad).reshape([-1,1])              # 勾配の変化量 (reshapeメソッドで列ベクトル化)
        Bs = np.dot(B, s)                                  # Bとsの内積
        B += (y*y.T)/np.dot(s.T, y) - (Bs*Bs.T)/np.dot(s.T, Bs)   # BFGS法による近似ヘッセ行列の更新

# 試行回数
print("done! ( i =", times, ")")
# 極小点の座標
print("(", X[0], ",", X[1],")")
# 極小点での値と勾配の大きさ
print("z =", f(X[0], X[1]), ", |d| =", np.linalg.norm(grad))

※「.T」というのは転置で、「np.dot(●, ×)」は●と×の内積を表しています。「np.linalg.inv(B)」で行列$\mathit{B}$の逆行列を計算しています。「.reshape([-1,1])」とすることで、列ベクトルに直すことができます。

初期座標を$(3.0,0.5)$としたときのニュートン法と準ニュートン法の実行結果を比較すると以下のようになります。

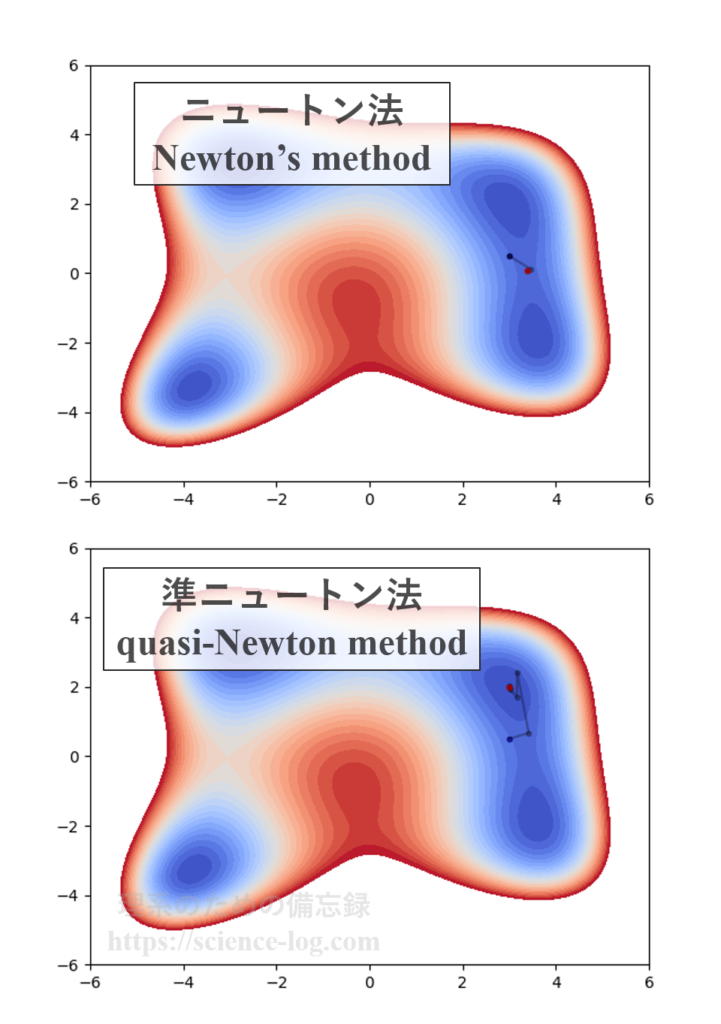
ニュートン法では鞍点に到達しているのに対して、準ニュートン法では極小点に到達しています。これより、準ニュートン法では同じ初期値を取ったとしても極小点を正しく見つけられることが分かります。

ヒンメルブラウの関数を準ニュートン法で最適化する場合、よほど直線探索のパラメータが悪くない限り、初期値を$(\pm 1.0,\pm 1.5)$とすれば全ての極小点が得られます。ヒンメルブラウの関数の停留点の座標については前回の「【最適化問題の基礎】ニュートン法で停留点を探す」の記事に掲載しています。

 

 まとめ

以上、ニュートン法を改良した準ニュートン法の概要について見てきました。準ニュートン法では2次収束ではなく「超1次収束」することが知られています。「点列$\{{\mathit{x}}_k\}$が超1次収束する」とは、ある最適解${\mathit{x}}^{\ast }$に対して、$${\displaystyle \underset{k\to \mathrm{\infty }}{lim}{\displaystyle \frac{\Vert {\mathit{x}}_{k+1}-{\mathit{x}}^{\ast }\Vert }{\Vert {\mathit{x}}_k-{\mathit{x}}^{\ast }\Vert }}=0}$$を満たすこと、と言い換えられます。これは、勾配法のように適切な降下方向を選択しつつも極小点付近ではニュートン法に匹敵する収束スピードを持つ、という良いとこ取りをしているイメージです。

有名どころの「共役勾配法」をスキップしてしまいましたが、ここまで制約無し連続最適化の初歩について（少し寄り道しつつ）概観してきました。準ニュートン法と並んで広く用いられている最適化手法の一つに「信頼領域法」という重要な手法があります。信頼領域法については次回以降取り扱っていこうと思います。