「順像法と逆像法」の第3弾です。今回は「線分」の掃過領域を扱います。前回に引き続き東京大学の問題を引っ張ってきていますが、こちらも良問なので志望大学に関わらず是非解いてみて下さい!
《問題》
座標平面の原点を$\mathrm{O}$で表す。
線分 $y=\sqrt{3} x$ $(0 \leqq x \leqq 2)$ 上の点$\mathrm{P}$と、線分 $y=-\sqrt{3} x$ $(-2 \leqq x \leqq 0)$ 上の点$\mathrm{Q}$が、線分$\mathrm{OP}$と線分$\mathrm{OQ}$の長さの和が$6$となるように動く。このとき、線分$\mathrm{PQ}$の通過する領域を $D$ とする。
(1)$s$ を $0 \leqq s \leqq 2$ をみたす実数とするとき、点$(s,t)$が$D$に入るような$t$の範囲を求めよ。
(2)$D$ を図示せよ。
(東京大学2014年 理科第6問)
《考え方》
本問には順像法による誘導設問が付いています。(2)は図示だけなので、実質的には(1)が解ければOKです。問題文には「点$(s,t)$が$D$に入るような$t$の範囲」とあるので「順像法」による解答が求められています。
肝心の図形ですが、問題設定の状況を図として想像できますか?
それぞれの点と線分の位置関係は下図のようになっています(点$\mathrm{P}$、$\mathrm{Q}$は動かせます)。
このグラフを見れば、まず直線$\mathrm{PQ}$の通過する領域を求め、そこから線分 $y=\sqrt{3} x$ と、線分 $y=-\sqrt{3} x$ の上側の領域を取り出せば良いことが分かります。まず直線$\mathrm{PQ}$の方程式を求めてから、$x$座標を $x=s$ と固定して$y$方向の値域を考えます。
なお、領域を求める手順について詳しく知りたい方は「【順像法と逆像法①】直線の掃過領域を例に理解する」の記事をご覧下さい!
解答例
(1)
$\mathrm{P}(p, \sqrt{3} p)$、$\mathrm{Q}(-q, \sqrt{3} q)$、$(0 \leqq p \leqq 2,\,0 \leqq q \leqq 2)$ と置くと、$$\mathrm{OP}=2p、\mathrm{OQ}=2q$$であり、$$\mathrm{OP}+\mathrm{OQ}=6$$より、$p+q=3$、すなわち$$q=3-p \quad \cdots ①$$が成り立つ。$①$より$p$、$q$の変域は$$1 \leqq p \leqq 2, \, 1 \leqq q \leqq 2 \quad \cdots ②$$となる。
また、直線$\mathrm{PQ}$の方程式は$$\small \begin{align}
y &= \dfrac{\sqrt{3}(p-q)}{p+q}(x-p)+\sqrt{3} p \\
\therefore y &= \dfrac{\sqrt{3}(p-3+p)}{3}(x-p)+\sqrt{3} p \\
\therefore y &= \dfrac{\sqrt{3}}{3}(2 p-3) x+2 \sqrt{3} p-\dfrac{2}{3} \sqrt{3} p^{2} \quad \cdots ③
\end{align}$$となる。
また、線分$\mathrm{PQ}$の通過領域は、直線$\mathrm{PQ}$の通過領域のうち、線分 $y=\sqrt{3} x$ $(0 \leqq x \leqq 2)$ の上側の領域と、線分 $y=-\sqrt{3} x$ $(-2 \leqq x \leqq 0)$ の上側の領域に属する部分である・・・(※)。
$x=s$($0 \leqq s \leqq 2$)と固定し、方程式$③$の右辺を$p$の関数$f(p)$と置くと、$$\small f(p) = -\dfrac{2}{3} \sqrt{3} p^{2}+\left(\dfrac{2 \sqrt{3}}{3} s+2 \sqrt{3}\right) p-\sqrt{3} s \quad \cdots ④$$となる。以下、$②$の範囲で $t = f(p)$ の値域を求める。
$④$は$$\small f(p)=-\dfrac{2 \sqrt{3}}{3}\left(p-\dfrac{s+3}{2}\right)^{2}+\dfrac{\sqrt{3}}{6} s^{2}+\dfrac{3 \sqrt{3}}{2}$$と平方完成できる。よって $t = f(p)$($1 \leqq p \leqq 2$)の値域を求めるには端点$f(1)$、$f(2)$ および、頂点$f\left(\dfrac{s+3}{2}\right)$の大小を調べればよい。ただし、頂点の$y$座標 $f\left(\dfrac{s+3}{2}\right)$ は $1 \leqq \dfrac{s+3}{2} \leqq 2$、すなわち $0 \leqq s \leqq 1 \,(\because s \geqq 0)$ のときにのみ最大値となり得ることに注意する。$$\small \begin{cases}
f(1)=-\dfrac{\sqrt{3}}{3} s+\dfrac{4}{3} \sqrt{3} \\
f(2)=\dfrac{\sqrt{3}}{3} s+\dfrac{4}{3} \sqrt{3} \\
f\left(\dfrac{s+3}{2}\right)=\dfrac{\sqrt{3}}{6} s^{2}+\dfrac{3 \sqrt{3}}{2}
\end{cases}$$これらのグラフを $0 \leqq s \leqq 2$ の範囲で描くと以下のようになる。
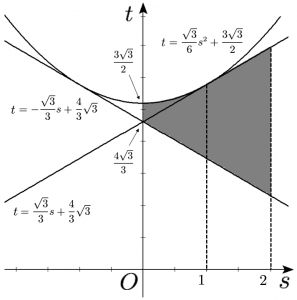
以上の領域および条件(※)を考慮し、$y=-\dfrac{\sqrt{3}}{3} x+\dfrac{4}{3} \sqrt{3}$ と $y=\sqrt{3} x$ の交点が$(1,\sqrt{3})$であることに注意すると、$0 \leqq s \leqq 2$ のとき点$(s,t)$が$D$に入るような$t$の範囲は、
$0 \leqq s \leqq 1$ のとき$$\small -\dfrac{\sqrt{3}}{3} s+\dfrac{4\sqrt{3}}{3} \leqq t \leqq \dfrac{\sqrt{3}}{6} s^{2}+\dfrac{3 \sqrt{3}}{2}$$
$1 < s \leqq 2$ のとき$$\small \sqrt{3}s \leqq t \leqq \dfrac{\sqrt{3}}{3} s+\dfrac{4\sqrt{3}}{3}$$となる。
※注:$0 \leqq s \leqq 2$ における$$\small \begin{cases} -\dfrac{\sqrt{3}}{3} s+\dfrac{4\sqrt{3}}{3} \leqq t \leqq \dfrac{\sqrt{3}}{6} s^{2}+\dfrac{3 \sqrt{3}}{2} \quad (0 \leqq s \leqq 1) \\ \sqrt{3}s \leqq t \leqq \dfrac{\sqrt{3}}{3} s+\dfrac{4\sqrt{3}}{3} \quad (1 < s \leqq 2) \end{cases}$$の範囲は以下のようになります。なお、$t=\dfrac{\sqrt{3}}{6} s^{2}+\dfrac{3 \sqrt{3}}{2}$ と $t=\dfrac{\sqrt{3}}{3} s+\dfrac{4\sqrt{3}}{3}$ は、点$\left(1,\dfrac{5\sqrt{3}}{3}\right)$で接しています。
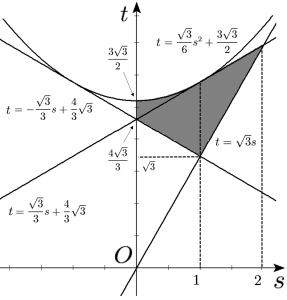
(2)
点$\mathrm{P}$、$\mathrm{Q}$の位置関係は$y$軸に関して対称であるから、領域 $D$ は$y$軸に関して対称である。よって(1)で求めた領域、および、これを$y$軸に関して折り返して得られる領域が $D$ である。したがって $D$ を図示すると、下図の網掛け部分となる。ただしすべての境界線を含む。

本問は順像法を使うように誘導設問が付いているので、幾分解きやすくなるように設計されています。順像法で解答するように指示されていますが、本問は逆像法でも解くことができます。
点$(X,Y)$を直線$\mathrm{PQ}$が通過するならば、解答例中の$③$式を変形して得られる$p$の二次方程式$$\small -\dfrac{2}{3} \sqrt{3} p^{2}+\left(\dfrac{2 \sqrt{3}}{3} X+2 \sqrt{3}\right) p-\sqrt{3} X-Y=0$$は少なくとも一つの実数解をもちます。このことから逆像法を用いて領域 $D$ を求めることができます。全く誘導が無い場合はこちらの方針で解答しても良いでしょう。
本問は誘導設問があるのでそれに従えば良いですね。領域 $D$ が$y$軸に関して対称となることは(1)が与えられていなくても見抜けることが望ましいです。難関大では、通過領域を求める問題が(毎年というほどの頻度ではないですが)出題されます(東大では割とよく出ます)。もし出題されたときに何の対策もしていないと悲惨な目に遭いますので、できるだけ対策しておきましょう!

“【順像法と逆像法③】線分の掃過領域(東京大学2014年)” への1件の返信