「順像法と逆像法」の解説シリーズも遂に最終回です。前回までは問題別に、方針の立て方から解答の方法、モノの見方などを色々と解説してきました。今回はこれまでの知識を踏まえ、実際に通過領域を求める問題に遭遇した際に、どの解法を選ぶのが適切なのかについて考察してみます。
これまでの復習
今までに以下の4題を扱ってきました。
※問題のタイトルがそのままリンクになっています。
正の実数$a$に対して、座標平面上で次の放物線を考える。$$C: \quad y=a x^{2}+\dfrac{1-4 a^{2}}{4 a}$$ $a$が正の実数全体を動くとき、$C$の通過する領域を図示せよ。
座標平面の原点を$\mathrm{O}$で表す。
線分 $y=\sqrt{3} x$ $(0 \leqq x \leqq 2)$ 上の点$\mathrm{P}$と、線分 $y=-\sqrt{3} x$ $(-2 \leqq x \leqq 0)$ 上の点$\mathrm{Q}$が、線分$\mathrm{OP}$と線分$\mathrm{OQ}$の長さの和が$6$となるように動く。このとき、線分$\mathrm{PQ}$の通過する領域を $D$ とする。
(1)$s$ を $0 \leqq s \leqq 2$ をみたす実数とするとき、点$(s,t)$が$D$に入るような$t$の範囲を求めよ。
(2)$D$ を図示せよ。
座標平面上の2点 $\mathrm{P}(t,\,t^{2})$、$\mathrm{Q}(t-5,\,t^{2}-4 t+2)$に対して $t$ が $1 \leqq t \leqq 3$ の範囲を動くとき、以下の各問いに答えよ。
問1 線分$\mathrm{PQ}$を表す直線の方程式および定義域を、$t$を用いて表せ(答えのみでよい)。
問2 線分$\mathrm{PQ}$が通過する範囲 $D$ を求め、図示せよ。
ここまで「順像法と逆像法シリーズ」の記事をご覧になった方にとってはお茶の子さいさいだと思いますが、もし不安要素があるならダッシュで確認しに行きましょう! ボリューム満点の解説を付けてあるので、まだ読んでいないという方も是非ご覧下さい!
確認のために順像法と逆像法の要点も再掲しておきます。
「順像法」の要点
① $x$(もしくは$y$)を固定する
② パラメータをすべての範囲にわたって動かし、$y$(もしくは$x$)の値のとりうる範囲(値域)を調べる
③ 得られた$x$、$y$の不等式から領域を決定する
順像法では点$(x,y)$を軸に平行な直線上に固定し、$a$の値を色々と動かして点の可動範囲をスキャンするように隈なく探す手法。基本的に全ての問題は順像法で解答可能。複雑な場合分けにも原理的には対応できる。
「逆像法」の要点
① 与方程式をパラメータについて整理する
② パラメータが実数として存在する条件を判別式などで求める
③ 得られた$x$、$y$の不等式から領域を決定する
パラメータを変数と見なして$x$、$y$の実数条件に読み替え、点$(x,y)$の存在領域をパラメータに関する方程式の解の配置問題に帰着して求める手法。ただし、逆像法はパラメータが1文字で2次以下、もしくは2文字でかつ対称式によって表せる場合に有効。複雑な場合分けはやや苦手。
さらに、解法選択の前提として
・基本的に全ての問題は順像法で解答可能(※一部例外あり)
・パラメータの範囲や点の存在範囲に制約が少ない場合は逆像法で一気に領域を求めるのがラク
順像法は素直
さて、上記の4題はいずれも順像法と逆像法の両方で解くことが可能でした。ただしその手間は問題によって異なります。
領域が多数種類の境界線を持つ場合は、場合分けが大変になります。言い換えると、大量の場合分けが必要な問題では図形の掃過領域が複雑であることが多いです。一概には言えませんが、そのような問題に対して逆像法を採用して解の配置問題に持ち込むと条件を捌くのが結構大変だったりします(例えば前回扱った日医大の問題など)。
また、方程式にパラメータが2文字以上含まれる場合、対称式にでも変換できない限り逆像法で太刀打ちするのは難しく、大抵は順像法が向いています。例えば次の問題を考えてみます。
東京大学2007年 理科第3問
座標平面上の2点 $\mathrm{P}$、$\mathrm{Q}$ が、曲線 $y=x^{2}$ $(-1 \leqq x \leqq 1)$ 上を自由に動くとき、線分$\mathrm{PQ}$を $1:2$ に内分する点$\mathrm{R}$が動く範囲を $D$ とする。ただし、$\mathrm{P=Q}$ のときは $\mathrm{R=P}$ とする。
(1)$a$ を $-1 \leqq a \leqq 1$ をみたす実数とするとき、点$(a,b)$が $D$ に属するための $b$ の条件を $a$ を用いて表せ。
(2)$D$ を図示せよ。
2点 $\mathrm{P}$、$\mathrm{Q}$ は自由に動き回るので、独立な実数のパラメータ $-1 \leqq p \leqq 1$、 $-1 \leqq q \leqq 1$ を用いて $\mathrm{P}(p,p^2)$、$\mathrm{Q}(q,q^2)$ と置くのは自然です。そうすると点$\mathrm{R}\left(\frac{2 p+q}{3}, \frac{2 p^{2}+q^{2}}{3}\right)$となり、もうこの時点で$p$と$q$の対称式では表せないことが分かるので、逆像法による方針はボツとなります。$$\left\{\begin{array}{l}
a=\dfrac{2 p+q}{3} \\
b=\dfrac{2 p^{2}+q^{2}}{3}
\end{array}\right.$$と置いて$q$を消去すると$$b=2 p^{2}-4 a p+3 a^{2}$$を得ます。これを$p$の二次方程式と見て $-1 \leqq p \leqq 1$ の範囲に実数解を持つ条件を調べてもよいのですが、消去した$q$の変域も考慮しなければならないので意外に骨が折れます。本問は順像法で解くのが一番素直でしょう。
※解答はここには掲載しません。基本的には$$f(p)=2(p-a)^2+a^2$$などと置いて軸の位置で場合分けして領域を求めることになります。$q$の変域を考慮すると、$p$の変域が一定ではないことに気が付くと思います。このようなパターンでは前回の【順像法と逆像法④】で解説した変域の捉え方が役に立ちます。
実数条件 V.S. 力業(円を含む場合)
これまで「基本的に全ての問題は順像法で解くことができます」と散々述べてきた訳ですが、やはり世の中には例外というのが付き物で、残念ながら順像法が不利になる問題も存在します。
例えば次の問題。
岐阜大学1989年など
$xy$平面上で曲線 $C:y=x^2$ $(x>0)$ 上の点$\mathrm{P}$を中心とし、$x$軸に接する円を考える。$\mathrm{P}$が$C$上を動くとき、この円の内部が動く範囲を図示せよ。
順像法でまともに解こうとしたら大変な目に遭います。というのも、$\mathrm{P}(p,p^2)$と置けば$$(x-p)^{2}+(y-p^{2})^{2}<p^{4}$$を満たすような点$(x,y)$の集合が求める領域に相当しますので、$p$について整理すると$$(1-2y)p^2-2xp+x^2+y^2<0$$となります。等式にして無理やり解くと、$$y=p^{2} \pm \sqrt{p^{4}-(x-p)^2}$$を得るので、これを $p>0$ の範囲で動かしたときの値域を求めることになります。しかしこれは無理関数であり、導関数は増減を調べられるような形にならず、式変形による解決もできないので、結局のところ順像法で解くのは困難です。
このような場合は、消去法的に逆像法(実数解$t$の存在条件に帰着させる方針)に頼るしかありません。それでも場合分けが少し面倒ではありますが…。
※なお、領域は以下の斜線部となります。ただし破線と白抜きの点は除きます。

また、次の問題も順像法だと難儀します。
2006年第2回東大実戦 文科第4問
放物線 $y=x^2$ 上の2点 $\mathrm{P}$、$\mathrm{Q}$ における接線が直交しているとき、線分 $\mathrm{PQ}$ を直径とする円を $C$ とする。
(1)円 $C$ の方程式を直線 $\mathrm{PQ}$ の傾き $m$ を用いて表せ。
(2)2点 $\mathrm{P}$、$\mathrm{Q}$ が動くとき、円 $C$ の通過する部分を求め、図示せよ。
(1)の結果は ↓↓↓ のようになります。
» (1) の答えはこちら
円 $C$:$\color{red}{x^{2}+y^{2}-m x-\left(m^{2}+\dfrac{1}{2}\right) y-\dfrac{3}{16}=0}$
» 閉じる
これもパラメータの式としては2次なので解けそうに見えます。しかし $x$、$y$ の式に円が含まれているので、$y$について解いてから順像法で処理するのはかなり困難です。なお、求めるべき通過領域は
$y \geqq -\dfrac{1}{4}$
かつ
$x^{2}+\left(y-\dfrac{3}{8}\right)^{2} \leqq \dfrac{9}{64}$
となります。
…というわけでパラメータの式に円が含まれる場合は逆像法がオススメです。
パラメータが高次の場合
例題①
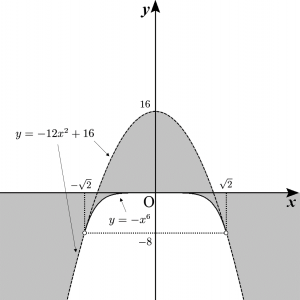
$t$が $0<t<2$ を満たして変化するとき、放物線$$y=2t^3-3t^2 x^2$$の通り得る領域を図示せよ。
実数$t$の3次式になっているので、実数解の存在条件を考えるのは難しいと判断。したがって $f(t)=2t^3-3t^2 x^2$ と置き、微分して値域を求めます(順像法を採用)。
答えとなる領域は下図の網掛け部分(境界は $y=-x^6$ $(|x|<\sqrt{2})$ の部分のみ含む)。
無理式を含む場合
例題②
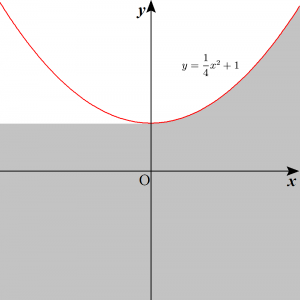
$t$が $t \geqq -1$ を満たして変化するとき、直線$$y=-t+\sqrt{t+1}\, x$$の通り得る領域を図示せよ。
この場合は結局$t$の2次方程式になるので、順像法と逆像法のどちらの方法でも解答可能です。
答えとなる領域は下図の網掛け部分(境界はすべて含む)。$y=\dfrac{1}{4}x^2+1$ は包絡線になっています。
パラメータに制約が少ない場合【重要】
名古屋大学1963年 文理共通第3問
点$\mathrm{P}$を通る直線を対称軸として、円 $x^2+y^2=1$ の対称図形をかいたとき、これが$x$軸に接した。このような点$\mathrm{P}$の存在範囲を求めよ。
点$\mathrm{P}$を$(X,Y)$、対称に写した円の中心を$(k,\pm 1)$などと置くと、諸々の関係式から$$k^{2}-2 X k+(1 \mp 2 Y)=0$$という方程式を得ます。逆像法だと判別式 $D \geqq 0$ から一気に存在範囲を求められます。これを順像法で解くと少し答案が長くなります。
y \geqq -\dfrac{1}{2}\left(x^{2}-1\right) \\
\text{または} \\
y \leqq \dfrac{1}{2}\left(x^{2}-1\right)
\end{cases}$$となります。
名古屋大学1978年 文系第4問
放物線 $y=-\dfrac{1}{3}x^2$ を、その頂点がいつも放物線 $y=x^2$ の上にあるように平行移動させる。こうして得られるどの放物線も通らない範囲を求め、図示せよ。
頂点が点$(t,t^2)$上に来るように平行移動した放物線の方程式は$$y=-\frac{1}{3}(x-t)^{2}+t^{2}$$であり、$$2 t^{2}+2 x t-(x^{2}+3 y)=0$$と整理できます。ここでどういうアプローチを取るかを決める訳ですが、問題文に「どの放物線も通らない範囲」とあるので、「そのような実数$t$の存在しない条件」を考えるのが適切です。そこで逆像法を用い、実数解を持たない条件 $D<0$ から一気に存在範囲を求めます。
なお、この領域は通過領域の補集合からも得られるので、必ずしも逆像法を使わなければならない訳ではありません。
このように、パラメータや点の存在範囲に制約があまり無い場合は逆像法で一気に領域を求めるのがラクです。勿論、順像法で解くことも可能ですが、パラメータの範囲に制約が無い場合は時間節約の意味でも逆像法をお勧めします。
他にも以下のような問題は逆像法でズバッと解決できます。
名古屋大学1965年 文理共通第3問
放物線 $y=1-x^2$ を平行移動させて、その頂点がもとの放物線 $y=1-x^2$ の上を動くようにする。このようにしてえられる放物線が存在する範囲を求めよ。
※答えは $y \leqq -\dfrac{1}{2}x^2+1$
名古屋大学1965年 文理共通第3問
$xy$平面上で次の条件を満たす点$\mathrm{P}$全体の集合を求め、これを図示せよ。
(条件)点$\mathrm{P}$の通る直線 $l$ で、$l$ と曲線 $y=x^2$ とで囲まれた部分の面積が $\dfrac{1}{6}$ となるものがある。
※答えは $y \leqq x^2+\dfrac{1}{4}$
図形的意味に着目する
最後にもう一題、見てみます。
例題③
$t$が任意の実数値をとるとき、座標平面上の2点$\mathrm{P}(t,t^2)$、$\mathrm{Q}(t+1,t^2+1)$を結ぶ線分の通過する領域を図示せよ。
まともに取り合うと面倒そうな問題ですが、図形的な意味を考えれば通過領域の見当を付けられることがあります。これは順像法とか逆像法とかいう以前の話です。
いま、線分$\mathrm{PQ}$は次のように動きます。
これにより、大雑把に次のような領域が得られるのではないかとアタリを付けることができます。
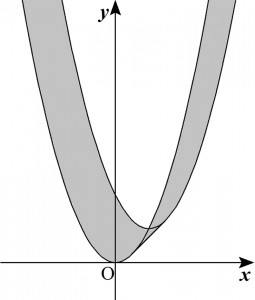
あらかじめ通過領域の目星が付いていれば、場合分けでミスして変な領域が得られても何かおかしいと気付くことができます。答えの見当が付いているかどうかというのは試験場では命運を分けるカギになることもあります。色々な視点から問題を観察できるようになっておきましょう。
因みに、この例題③の類題が大阪大学1985年文系第3問に出題されています。こちらは辺が1の正方形が曲線 $y=x^2$ と共有点をもつ、という条件がテーマの問題です。
(2022/02/03追記:文章のスタイルを一部変更)

通過領域シリーズは以上で一旦区切りとします。連日5本立てでお送りしてきましたが、その中の一つでも役立つ記事を見つけて頂ければ幸いです。通過領域の問題は一般的な教科書ではほとんど触れられておらず、解き方を知らないと全く手に負えないのが普通です。是非とも本シリーズを通じて対策し、この手の問題を苦手克服どころか得点源にしてライバルに差を付けてしまいましょう!