【高校数学】ベクトルの1次独立と1次従属

今回はベクトルの1次独立と1次従属に関するまとめです。

 

---

まずは定義を確認しましょう。

「1次独立」というのは「線形独立」と呼ばれることもあり、「ゼロベクトルの表示が自明なものに限ること」と言い換えることができます。また、「1次従属」は「線形従属」と呼ばれることもあります。次の課程の高校数学ではベクトルが

●　　　●　　　●

具体的な例で考えてみます。

例えば、$$\vec{a}=\left[\begin{array}{c}
1 \\
0 \\
0
\end{array}\right], \ \vec{b}=\left[\begin{array}{c}
0 \\
1 \\
0
\end{array}\right], \ \vec{c}=\left[\begin{array}{c}
0 \\
0 \\
1
\end{array}\right]$$の線形結合が零ベクトルになる、即ち$$k\,\vec{a}+l\,\vec{b}+m\,\vec{c}=\vec{0}$$となるような実数 $k$、$l$、$m$ の組は $k=l=m=0$ に限ります。

一方で、$\vec{a}$、$\vec{b}$、$\vec{c}$ が同一平面上のベクトルであるとき、例えば $k$、$l$、$m$ のうち $m \ne 0$ であれば、ある実数 $k^{\prime}$、$l^{\prime}$ を用いて$$\vec{c}=k^{\prime} \vec{a}+l^{\prime} \vec{b}$$と表せて、$$k^{\prime} \vec{a}+l^{\prime} \vec{b}+(-1) \vec{c}=\vec{0}$$となるので、$\vec{a}$、$\vec{b}$、$\vec{c}$ は1次従属です。例えば、$$\vec{a}=\left[\begin{array}{c}
1 \\
-1 \\
0
\end{array}\right], \ \vec{b}=\left[\begin{array}{c}
0 \\
1 \\
-1
\end{array}\right], \ \vec{c}=\left[\begin{array}{c}
1 \\
0 \\
-1
\end{array}\right]$$の場合、$k=l=1$、$m=-1$ とすれば$$k\,\vec{a}+l\,\vec{b}+m\,\vec{c}=\vec{0}$$が成り立つので、$\vec{a}$、$\vec{b}$、$\vec{c}$ は1次従属です。

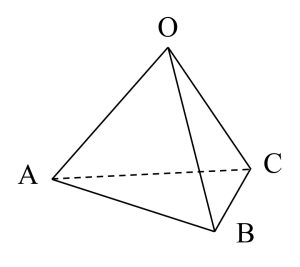
以上のことから、$\vec{a}$、$\vec{b}$、$\vec{c}$ が1次独立のときは、$\mathrm{OA}=|\vec{a}|$、$\mathrm{OB}=|\vec{b}|$、$\mathrm{OC}=|\vec{c}|$ とすると、四面体 $\mathrm{OABC}$ を作ることができます。逆に、四面体の3脚であるような $\vec{\mathrm{OA}}$、$\vec{\mathrm{OB}}$、$\vec{\mathrm{OC}}$ は1次独立となります。

●　　　●　　　●

3次元ベクトルの場合についてまとめておきます。

①「$\vec{a}$、$\vec{b}$、$\vec{c}$ が1次独立」と次の３つは同値

1. $k \vec{a}+l \vec{b}+m \vec{c}=\vec{0}$ が成り立つのは、$k=l=m=0$ に限る。
   　
2. $k \vec{a}+l \vec{b}+m \vec{c}=k’ \vec{a}+l’ \vec{b}+m’ \vec{c}$ が成り立つのは、$k=k’$、$l=l’$、$m=m’$ に限る。
   　
3. 空間内の任意のペクトル $\vec{d}$ は$\vec{d}=\alpha \vec{a}+\beta \vec{b}+\gamma \vec{c}$ （$\alpha$、$\beta$、$\gamma$は実数）とただ1通りに表される。
   ※このとき、$\langle\vec{a}, \vec{b}, \vec{c}\rangle$ を基底、($\alpha, \beta, \gamma$) を基底に関する $\vec{d}$ の成分という。

●　　　●　　　●

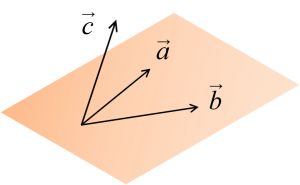
②「$\vec{a}$、$\vec{b}$、$\vec{c}$ が1次従属」と次は同値

• $k \vec{a}+l \vec{b}+m \vec{c}=\vec{0}$ を満たす少なくとも1つは$0$でない $k$、$l$、$m$ が存在する。

 

---

2次元ベクトルは平面のベクトル、3次元ベクトルは空間のベクトルとして考えればイメージしやすいですが、4次元ベクトルやそれ以上の高次のベクトルについても「1次独立/従属」が同様に定義されます。一般の$n$次ベクトルの場合について、「線形従属でない」＝「線形独立」と説明している参考書も多いです。