2025年の共通テスト数学ⅠAの第1問を解説します。
(1) $a, b$ を実数とする。$x$ についての方程式
\begin{equation}
(2a + 4b-2)x^2 + (5a + 11)x-b-8 = 0 \tag{①}
\end{equation}を考える。
(1) $a = 1$ とする。
$b$ に着目すると、①の左辺は
\begin{equation}
(4x^2-1)b + 16x-8 \tag{②}
\end{equation}と表せる。よって、②を因数分解すると
\[
(2x-1)\left(\boxed{ア} \, b \, x + b + \boxed{イ}\right)
\]となる。したがって、$x = \dfrac{1}{2}$ は①の解の一つであることがわかる。
(2) $b = 2$ とする。
(i) ①の左辺を因数分解すると
\[
(\boxed{\text{ウ}}x + \boxed{\text{エ}})\{(a + \boxed{\text{オ}})x-\boxed{\text{カ}}\}
\]となる。
(ii) $a = 2\sqrt{2}$ のとき、①の解は
\[
x = -\dfrac{\boxed{\text{エ}}}{\boxed{\text{ウ}}}, \quad \boxed{\text{キ}}-\boxed{\text{ク}}\sqrt{2}
\]となる。
(iii) $a = -\boxed{\text{オ}}$ であることは、①の解が $x = -\dfrac{\boxed{\text{エ}}}{\boxed{\text{ウ}}}$ だけであるための $\boxed{\text{ケ}}$。
$\boxed{\text{ケ}}$ の解答群:
⓪ 必要条件であるが、十分条件ではない
① 十分条件であるが、必要条件ではない
② 必要十分条件である
③ 必要条件でも十分条件でもない
(2025年 共通テスト数学ⅠA 本試験第1問〔1〕)
考え方・解答例
(1)
$a = 1$ のとき、問題文の通り$$(4x^2-1)b + 16x-8$$が得られます。これを次のように因数分解します。
まず、$4x^2-1 = (2x + 1)(2x-1)$ および $16x-8 = 8(2x-1)$ となるので
\begin{aligned} & \quad (4x^2-1)b + 16x-8 \\ &= b \cdot (2x + 1)(2x-1) + 8(2x-1) \\ &= (2x-1) \left( (2x + 1)b + 8 \right) \end{aligned}
と整理できます。問題では
\[
(2x-1)(\boxed{\text{ア}} b x + b + \boxed{\text{イ}})
\]としているので、実際比較すると
\[
(2x + 1)b + 8 = b(2x) + b + 8 = 2bx + (b + 8).
\]よって「$\boxed{\text{ア}} = 2, \boxed{\text{イ}} = 8$」と分かります。
また、この因数 $(2x-1)$ が含まれるため、$(2x-1) = 0 \implies x = \dfrac{1}{2}$ が (1) の根の1つであることがわかります。
(2)
(ⅰ)式に $b = 2$ を代入すると
\[
(2a + 4 \cdot 2-2)x^2 + (5a + 11)x-(2 + 8) = 0,
\]すなわち
\[
(2a + 8-2)x^2 + (5a + 11)x-10 = 0
\]\[
\therefore (2a + 6)x^2 + (5a + 11)x-10 = 0.
\]を得ます。
問題文によるとこれは次のように因数分解できるようです。
\[
(\boxed{\text{ウ}}x + \boxed{\text{エ}})\{(a + \boxed{\text{オ}})x-\boxed{\text{カ}}\}
\]後者の因数の$a$の係数が$1$になっていることから、$2$で括り出していると考えられます。また、定数項が$10$なので$\boxed{\text{エ}}$と$\boxed{\text{カ}}$の組み合わせは、$1$と$10$、または$2$と$5$のいずれかに限られます。
左辺について、$$2(a + 3)x^2 + \{5(a + 3)-2 \cdot 2\}x-10$$ つまり$$(2x + 5)\{(a + 3) x-2\}$$と因数分解できることが分かるので、「$\boxed{\text{ウ}} = 2$, $\boxed{\text{エ}} = 5$, $\boxed{\text{オ}} = 3$, $\boxed{\text{カ}} = 2$」と分かります。
(ⅱ)続いて $a = 2\sqrt{2}$ のとき、先程の因数分解の式から、解は$$x=-\dfrac{5}{2}, \ \dfrac{2}{3+2\sqrt{2}}$$と分かります。後者の分母を有理化すると、$\dfrac{2(3-2\sqrt{2})}{(3+2\sqrt{2})(3-2\sqrt{2})}$ すなわち $6-4\sqrt{2}$ を得ます。よって「$\boxed{\text{キ}} = 6$, $\boxed{\text{ク}} = 4$」と分かります。
(ⅲ)$a=-3$ のとき、先程の因数分解の式から与方程式は$$-2(2x+5)=0$$になります。したがって「$a=-3$ ⇒ ①の解が$x=-\dfrac{5}{2}$だけである」が成り立つので、十分条件です。
一方で、①は2次方程式なので解が$x=-\dfrac{5}{2}$だけである場合というのは、他に「$x=-\dfrac{5}{2}$が①の重解である」場合が考えられます。そこで $x=\dfrac{2}{a+3}$ が $x=-\dfrac{5}{2}$ に一致するような$a$の値が存在することを確かめます。実際、そのような$a$は存在し($a=-\dfrac{19}{5}$)、必要条件ではないことが分かります(下記☑POINTを参照のこと)。
よって、「$\boxed{\text{ケ}} = 1$」となります。
包含関係のイメージとしては以下のようになっているため、「①の解が$x=-\dfrac{5}{2}$だけである ⇒ $a=-3$ である」が成り立つわけではありません。したがって「十分条件であるが、必要条件ではない」が正しい答えとなります。 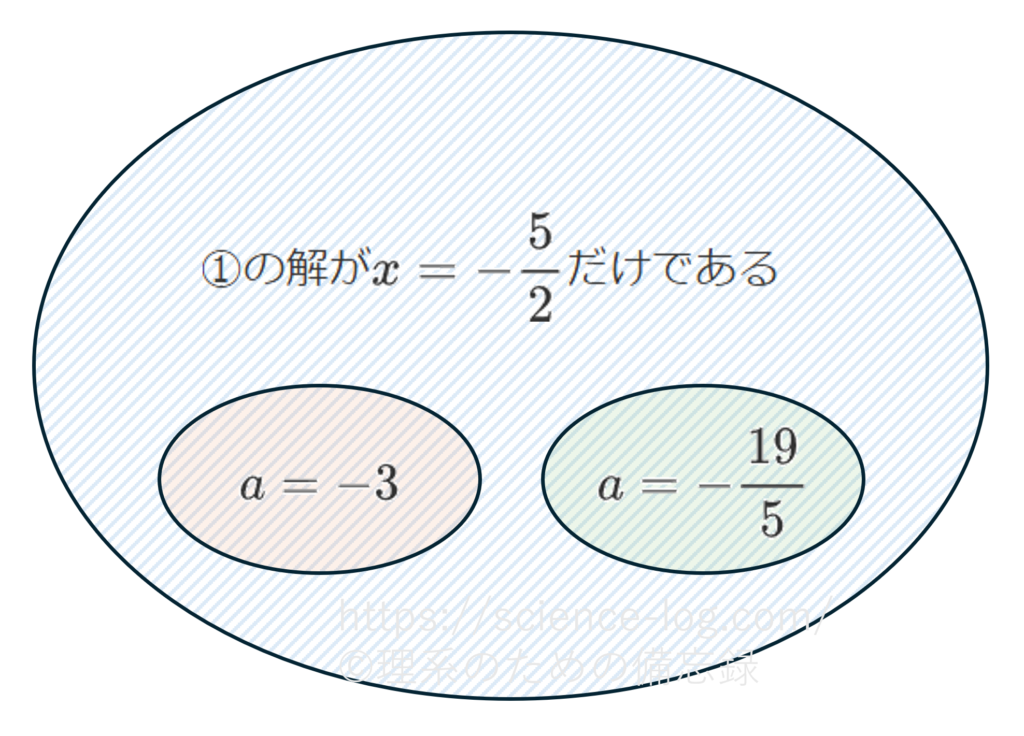
なお、包含関係で図示したときに領域が包含される方の条件を「十分条件」と言い、外側の条件は「必要条件」と言います。
図1のように、直線$\ell$上の点$A$において$\ell$に接する半径$2$の円を円$O$とし、$\ell$上の点$B$において$\ell$に接する半径$4$の円を円$O’$とする。円$O$と$O’$は2点で交わるとし、その交点を$P, Q$とする。ただし、$\angle APB < \angle AQB$とする。また、$\angle PAB$は鋭角であるとする。このとき、$\triangle PAB$と$\triangle QAB$について考えよう。
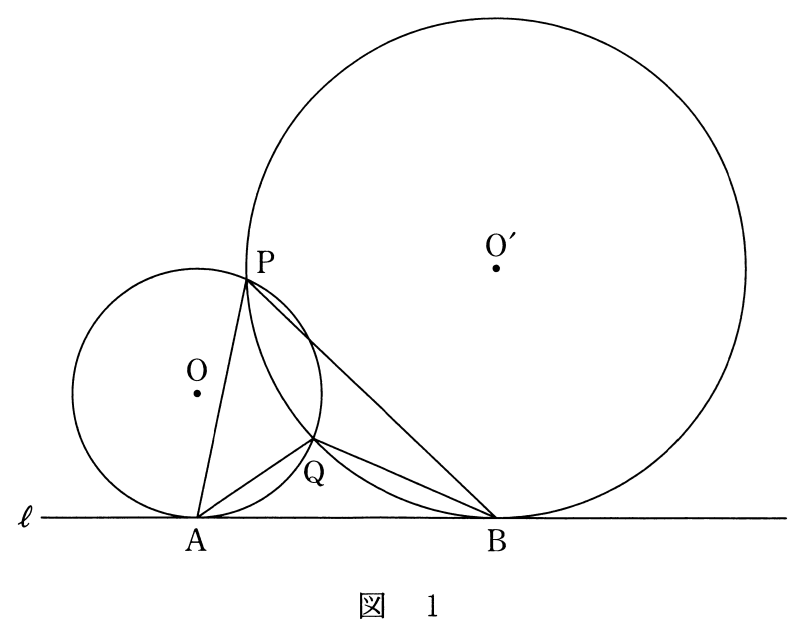
(1) $\angle PAB = \alpha$, $\angle PBA = \beta$ とおく。
円$O$の中心$O$から直線$PA$に引いた垂線と直線$PA$との交点を$H$とする。$\angle OAB = 90^\circ$であるから、$\angle AOH = \alpha$である。よって、$\triangle AOH$に着目すると、$AH = \boxed{\text{コ}} \sin \alpha$ であるから、
\[
PA = 2 \cdot AH = \boxed{\text{サ}} \sin \alpha \tag{①}
\]である。
同様にして、円$O’$の中心$O’$から直線$PB$に引いた垂線と直線$PB$との交点を$H’$とすると
\[
PB = 2 BH’ = \boxed{\text{シ}} \sin \beta \tag{②}
\]であることもわかる。
また、$\triangle PAB$の外接円の半径を$R_1$とおくと、正弦定理により
\[
\frac{\text{PA}}{\sin \boxed{\text{ス}}} = \frac{\text{PB}}{\sin \boxed{\text{セ}}} = 2R_1
\]が成り立つので
\[
\text{PA} \sin \boxed{\text{セ}} = \text{PB} \sin \boxed{\text{ス}}
\]である。この式に、①と②を代入することにより
\[
\sin \boxed{\text{セ}} = \sqrt{\boxed{\text{ソ}}} \sin \boxed{\text{ス}}
\]\[
PB = \sqrt{\boxed{\text{ソ}}} \cdot PA
\]となることがわかる。さらに
\[
R_1 = \boxed{\text{タ}} \sqrt{\boxed{\text{チ}}}
\]が得られる。
$\boxed{\text{ス}}, \boxed{\text{セ}}$ の解答群(同じものを繰り返し選んでもよい。)
⓪ $\alpha$ ① $\beta$
(2) 太郎さんと花子さんは、(1)の考察を振り返っている。
太郎:「$\triangle QAB$の外接円の半径も求められるかな。」
花子:「(1)の$R_1$の求め方を参考にすればよさそうだね。」
$\triangle PAB, \triangle QAB$の外接円の半径をそれぞれ$R_1, R_2$とおく。このとき、$R_1 \boxed{\text{ツ}} R_2$ である。さらに、$\sin \angle APB \boxed{\text{テ}} \sin \angle AQB$であることもわかる。
$\boxed{\text{ツ}}, \boxed{\text{テ}}$ の解答群(同じものを繰り返し選んでもよい。)
⓪ < ① = ② >
(3) 太郎さんと花子さんは、これまでの考察をもとに、$\triangle PAB$ と $\triangle QAB$ の辺の長さについて考えている。
太郎: $AB$ の長さが与えられれば、$PA$ と $QA$ の長さが求められそうだね。
花子: $\angle APB < \angle AQB$ に注意して求めてみようよ。
$AB = 2\sqrt{7}$ とする。このとき
\[
\sin \angle APB = \frac{\sqrt{\boxed{\text{トナ}}}}{\boxed{\text{ニ}}}
\]である。(1)より、
\[
PB = \sqrt{\boxed{\text{ソ}}} \cdot PA
\]であるから
\[
PA = \sqrt{\boxed{\text{ヌネ}}}
\]である。
同様に、
\[
QA = \sqrt{7}
\]であることがわかる。
(2025年 共通テスト数学ⅠA 本試験第1問〔2〕)
考え方・解答例
(1)
円$O$の半径は$2$なので $AH = 2 \sin \alpha$ と表せて、$$PA = 2 \cdot AH = 4 \sin \alpha$$となります。また、同様に円$O’$の半径は$4$なので $BH’ = 4 \sin \beta$ と表せて、$$PB = 2 \cdot BH’ = 8 \sin \beta$$となります。よって「$\boxed{\text{コ}} = 2$, $\boxed{\text{サ}} = 4$, $\boxed{\text{シ}} = 8$」と分かります。
正弦定理より$$\dfrac{\text{PA}}{\sin \beta} = \dfrac{\text{PB}}{\sin \alpha} = 2R_1$$が成り立つので①式と②式より$$4\sin^2 \alpha=8\sin^2 \beta$$となります。ここで $\sin \alpha$ と $\sin \beta$ はともに正なので両辺の平方をとって$$2\sin \alpha=2 \sqrt{2}\sin \beta$$ $$\therefore \sin \alpha=\sqrt{2}\sin \beta$$を得ます。よって正弦定理および $\dfrac{\sin \alpha}{\sin \beta}=\sqrt{2}$ より$$R_1=\dfrac{4 \sin \alpha}{2 \sin \beta}=2\sqrt{2}$$と求められます。
よって「$\boxed{\text{ス}} = 1$, $\boxed{\text{セ}} = 0$, $\boxed{\text{ソ}} = 2$, $\boxed{\text{タ}} = 2$, $\boxed{\text{チ}} = 2$」と分かります。
(2)
次に$\triangle QAB$の外接円について考えます。ヒントにあるように$R_1$と同様に考えます。
円$O$の中心$O$から直線$QA$に引いた垂線と直線$QA$との交点を$H_a$とすると、\[
QA = 2 \cdot AH_a = 4 \sin \alpha \tag{③}
\]となります。また、円$O’$の中心$O’$から直線$QB$に引いた垂線と直線$QB$との交点を$H_b$とすると、\[
QB = 2 \cdot BH_b = 8 \sin \beta \tag{④}
\]となります。
ここで、先程と全く同じ関係式が得られていることに気が付くはずです。実は全く同様の処理により、$R_2=2\sqrt{2}$と求められ、$R_1=R_2$ が成り立ちます。ここで$\triangle PAB$と$\triangle QAB$のそれぞれで正弦定理から$$\begin{cases} 2R_1=\dfrac{AB}{\sin \angle APB} \\ 2R_2=\dfrac{AB}{\sin \angle AQB} \end{cases}$$が成り立ちますが、いま $R_1=R_2$ なので $$\dfrac{AB}{\sin \angle APB}=\dfrac{AB}{\sin \angle AQB}$$すなわち$$\sin \angle APB=\sin \angle AQB$$が成り立ちます。
よって「$\boxed{\text{ツ}} = 1$, $\boxed{\text{テ}} = 1$」と分かります。
(3)
$\triangle PAB$について正弦定理より $\dfrac{AB}{\sin \angle APB}=2 R_1$ が成り立つから、$AB = 2\sqrt{7}$ のとき、$R_1=2 \sqrt{2}$より$$\sin \angle APB=\dfrac{\sqrt{14}}{4}$$となります。よって、$\angle APB$が鋭角であることに注意すれば$$\cos \angle APB=\dfrac{\sqrt{2}}{4}$$と求められます。
ここで余弦定理$$AB^2=PA^2+PB^2-2 PA \cdot PB \cos \angle APB$$より、$$28=PA^2+2PA^2-2\sqrt{2}PA^2 \cdot \dfrac{\sqrt{2}}{4}$$ $$\therefore PA^2= 14$$ $$\therefore PA=\sqrt{14}$$を得ます。
よって「$\boxed{\text{ト}} = 1$, $\boxed{\text{ナ}} = 4$, $\boxed{\text{ニ}} = 4$, $\boxed{\text{ヌ}} = 1$, $\boxed{\text{ネ}} = 4$」と分かります。
それなりに長めの問題ですが、中身はかなりシンプルな内容でした。今年の数ⅠAは易化傾向なので、第1問は落としたくない設問です。
全体的に誘導が丁寧で解きやすかったのではないかと思いますが、誘導が丁寧だとむしろ解きにくいと感じる人もいるかもしれません。そういう場合は誘導を完全に無視してしまうのも一つの手です。(ただ、共通テストは穴埋め式のマークシート問題なので、誘導に従う方が効率的に解答できるという点には留意しておきましょう)
問題〔1〕で困るところはあまり無いと思いますが、必要十分性についての理解が曖昧、もしくは重解の可能性に気が付けないと(ⅲ)で失点してしまったかもしれません。
問題〔2〕は図形の問題でした。計算も比較的平易で、ミスなく得点したいところです。強いて言えば(2)で少し焦ってしまった受験生がいたかもしれませんね。平面図形の問題で使うべき道具は大体決まっているので、落ち着いて立式したいところです。

“【2025年】共通テスト数学ⅠA第1問” への2件の返信