【2025年】共通テスト数学ⅠA第2問〔２〕

2025年の共通テスト数学ⅠAの第2問〔２〕（後半の問題）を解説します。問題文が長いので、複数タブを開くか手元に問題用紙を用意すると良いかもしれません。

第２問〔２〕

以下の問題を解答するにあたっては、与えられたデータに対して、次の値を外れ値とする。

(第1四分位数) - 1.5 \times (四分位範囲) \leq 以下の値

(第3四分位数) + 1.5 \times (四分位範囲) \geq 以上の値

太郎さんは、47都道府県における外国人宿泊者数と日本人宿泊者数の動向を調べるため、それらに関するデータを分析することにした。外国人宿泊者数を、日本国内に住所を有しない宿泊者の人数の1年間の合計とし、日本人宿泊者数を、日本国内に住所を有する宿泊者の人数の1年間の合計とする。宿泊者数に関するデータは千の位を四捨五入し、1万人単位で表したものとし、以下においては単位（万人）を省略して用いることとする。例えば、「4567890人」は「457」とする。

なお、以下の図や表については、国土交通省のWebページをもとに作成したものである。

（１）

(i) 図1は、47都道府県における令和4年の外国人宿泊者数と日本人宿泊者数の散布図である。なお、散布図には原点を通り、傾きが10の直線（破線）を付加している。また、日本人宿泊者数が1000を超える都道府県の数は12である。

図１　令和4年の外国人宿泊者数と日本人宿泊者数の散布図

次の (a), (b) は、図1に関する記述である。

(a)　令和4年について、外国人宿泊者数が100を超え、かつ日本人宿泊者数が2500を超える都道府県の数は2である。
(b)　令和4年について、日本人宿泊者数が外国人宿泊者数の10倍未満である都道府県の割合は50%未満である。

(a), (b) の正誤の組み合わせとして正しいものは $タ$ である。

$タ$ の解答群

	⓪	①	②	③
(a)	正	正	誤	誤
(b)	正	誤	正	誤

(ii)　

47都道府県における令和4年の外国人宿泊者数を分析した結果、外れ値となる都道府県の数は8であった。

一方、表1は47都道府県における令和4年の日本人宿泊者数を、値の小さい順に並べ、その順に都道府県 $P_{1}, P_{2}, \dots, P_{47}$ としたものである。この中で、外国人宿泊者数で外れ値となる都道府県( $P_{37}, P_{40}, P_{42}, P_{43}, P_{44}, P_{45}, P_{46}, P_{47}$ )に印 * を付けている。

表１　47都道府県における令和4年の日本人宿泊者数

都道府県	日本人宿泊者数	都道府県	日本人宿泊者数	都道府県	日本人宿泊者数
P₁	182	P₁₃	373	P₂₅	620
P₂	187	P₁₄	388	P₂₆	625
P₃	197	P₁₅	395	P₂₇	646
P₄	204	P₁₆	401	P₂₈	670
P₅	255	P₁₇	405	P₂₉	683
P₆	270	P₁₈	452	P₃₀	705
P₇	276	P₁₉	458	P₃₁	831
P₈	303	P₂₀	501	P₃₂	832
P₉	303	P₂₁	522	P₃₃	839
P₁₀	321	P₂₂	537	P₃₄	876
P₁₁	328	P₂₃	605	P₃₅	925
P₁₂	351	P₂₄	613	P₃₆	1251
P₃₇*	1339	P₄₀*	1765	P₄₃*	2158
P₃₈	1399	P₄₁	1814	P₄₄*	2195
P₃₉	1547	P₄₂*	1970	P₄₅*	2831
P₄₆*	2839	P₄₇*	5226

表1のデータにおいて、四分位範囲は
$チ$ となることから、令和4年の外国人宿泊者数と日本人宿泊者数の両方で外れ値となる都道府県の数は
$ツ$ である。

$チ$ の解答群

⓪	320	①	450	②	597	③	638	④	900
⑤	966	⑥	1253	⑦	1261	⑧	1602	⑨	1864

（２）

47都道府県におけるある年の外国人宿泊者数を $x$ 、日本人宿泊者数を $y$ とし、 $x$ と $y$ の値の組を、それぞれ
$(x_{1}, y_{1}), (x_{2}, y_{2}), \dots, (x_{47}, y_{47})$ と表す。 $x, y$ の平均値をそれぞれ $\overset{―}{x}, \overset{―}{y}$ とし、 $x, y$ の分散をそれぞれ $s_{x}^{2}, s_{y}^{2}$ とする。また、 $x$ と $y$ の共分散を $s_{x y}$ とする。

47都道府県それぞれにおける外国人宿泊者数と日本人宿泊者数を足し合わせた合計宿泊者数を $z$ とし、その値を
$z_{i} = x_{i} + y_{i} (i = 1, 2, \dots, 47)$ と表す。例えば、 $i = 7$ のときは $z_{7} = x_{7} + y_{7}$ である。

$z$ の平均値を $\overset{―}{z}$ とするとき、
$z_{i} - \overset{―}{z} = (x_{i} - \overset{―}{x}) + (y_{i} - \overset{―}{y}) (i = 1, 2, \dots, 47)$ である。このことに着目すると、 $z$ の分散を $s_{z}^{2}$ とするとき、
$s_{z}^{2} = テ$ となる。

また、令和4年の $x$ と $y$ の間には正の相関があることが図1からわかる。このことから、令和4年について、 $s_{z}^{2}$ と $s_{x}^{2} + s_{y}^{2}$ の関係として、後の ⓪ ～ ② のうち、正しいものは
$ト$ であることがわかる。（図１の再掲は省略）

$テ$ の解答群
$\begin{array}{ll} ⓪ & s_{x}^{2} + s_{y}^{2} - 2 s_{x y} \\ ① & s_{x}^{2} + s_{y}^{2} - s_{x y} \\ ② & s_{x}^{2} + s_{y}^{2} \\ ③ & s_{x}^{2} + s_{y}^{2} + s_{x y} \\ ④ & s_{x}^{2} + s_{y}^{2} + 2 s_{x y} \end{array}$

$ト$ の解答群
$\begin{array}{ll} ⓪ & s_{z}^{2} > s_{x}^{2} + s_{y}^{2} \\ ① & s_{z}^{2} = s_{x}^{2} + s_{y}^{2} \\ ② & s_{z}^{2} < s_{x}^{2} + s_{y}^{2} \end{array}$

（３）

太郎さんが住む地域では、その地域に宿泊を促すためのキャンペーンとして、キャンペーンA、Bが実施されている。

太郎さんは、キャンペーンAの方がよいと思っている人が多いという噂を聞いた。このうわさのとおり、キャンペーンAの方がよいと思っている人が多いといえるかどうかを確かめることにした。そこで、かたよりなく選んだ人たちに、キャンペーンA、Bのどちらがよいかについて、二択のアンケートを行ったところ、アンケートに回答した35人のうち、23人が「キャンペーンAの方がよい」と答えた。この結果から、一般にキャンペーンAの方がよいと思っている人が多いといえるかどうかを、次の方針で考えることにした。

【方針】

・“「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい” という仮説を立てる。

・この仮説のもとで、かたよりなく選ばれた35人のうち23人以上が「キャンペーンAの方がよい」と回答する確率が5%未満であれば、その仮説は誤っていると判断し、5%以上であればその仮説は誤っているとは判断しない。

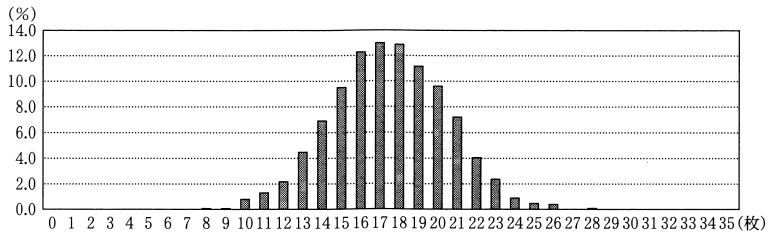
後の実験結果は、35枚の硬貨を投げる実験を1000回行ったとき、表が出た枚数ごとの回数の割合を示したものである。

実験結果

表の枚数(枚)	0	1	2	3	4	5	6	7	8	9	10	11
割合(%)	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.1	0.1	0.8	1.3
表の枚数(枚)	12	13	14	15	16	17	18	19	20	21	22	23
割合(%)	2.2	4.5	6.9	9.5	12.3	13.0	12.9	11.2	9.6	7.2	4.1	2.4
表の枚数(枚)	24	25	26	27	28	29	30	31	32	33	34	35
割合(%)	0.9	0.5	0.4	0.0	0.1	0.0	0.0	0.0	0.0	0.0	0.0	0.0

表の枚数

実験結果を用いると、35枚の硬貨のうち23枚以上が表となった割合は、 $ナ . ニ$ %である。これを、35人のうち23人以上が「キャンペーンAの方がよい」と回答する確率とみなし、方針に従うと、
「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい」という仮説は $ヌ$ 。したがって、今回のアンケート結果からは、キャンペーンAの方がよいと思っている人が $ネ$ 。

$ヌ$ 、 $ネ$ については、最も適当なものを、次のそれぞれの解答群から一つずつ選べ。

$ヌ$ の解答群
$\begin{array}{cc} ⓪ & 誤っていると判断する \\ ① & 誤っているとは判断しない \end{array}$

$ネ$ の解答群
$\begin{array}{cc} ⓪ & 多いといえる \\ ① & 多いとはいえない \end{array}$

（2025年共通テスト数学ⅠA 本試験第2問〔２〕）

考え方・解答例

（１）

（ⅰ）1問目は散布図に関する問題です。

(a)の主張は「外国人宿泊者数が100を超えている」かつ「日本人宿泊者数が2500を超えている」なので、該当するのは下図の赤色部分となります。領域内の点は2つですから、(a)は「正しい」と分かります。

(b)についてですが、グラフ上の対角線がちょうど10倍の線にあたります。見たところ、この直線より下にある点は1つしかないので、(b)の主張「日本人宿泊者数が外国人宿泊者数の10倍未満である都道府県の割合は50%未満」は正しいことがわかります。

よって、正、正なので「 $タ = 0$ 」と分かります。

（ⅱ）データは47個で奇数個存在するので中央値は $P_{24}$ となり、中央値を挟んで両側23個ずつに分けられます。これも奇数なので四分位数は $12$ 、 $36$ と分かります。箱ひげ図のイメージとしては以下のようになります。

よって四分位範囲は $P_{36}$ と $P_{12}$ の値の差を取ればよく、 $1251 - 351 = 900$ と分かります。

今回、外れ値の定義は以下のようなものでした。これに従って計算します。

$(第1四分位数) - 1.5 \times (四分位範囲) \leq 以下の値$ $(第3四分位数) + 1.5 \times (四分位範囲) \geq 以上の値$

第１四分位について、 $351 - 1.5 \times 900$ は負なので、小さい方の外れ値は存在しないことが分かります。続いて第３四分位について、計算すると $1251 + 1.5 \times 900 = 2601$ より、これより大きなものはP₄₅*、P₄₆*、P₄₇*の3都道府県しかないことが分かります。

よって、「 $チ = 4$ 、 $ツ = 3$ 」となります。

（２）

分散と共分散の定義が頭に入っていれば簡明な問題です。

$z_{i} = x_{i} + y_{i} (i = 1, 2, \dots, 47)$ という定義から、 $z$ の共分散は $S_{z}^{2} = \frac{1}{47} {{(z_{1} - \bar{z})}^{2} + \dots + {(z_{47} - \bar{z})}^{2}}$ と表せます。ここで、 $\begin{aligned} {(z_{i} - \bar{z})}^{2} & = {(x_{i} - \bar{x}) + (y_{i} - \bar{y})}^{2} \\ = {(x_{i} - \bar{x})}^{2} + {(y_{i} - \bar{y})}^{2} + 2 (x_{i} - \bar{x}) (y_{i} - \bar{y}) \end{aligned}$ と展開できるので、 $i = 1, 2, \dots, 47$ について和をとれば $S_{z}^{2} = S_{x}^{2} + S_{y}^{2} + 2 S_{x y} > S_{x}^{2} + S_{y}^{2}$ であることが分かります。ここで、不等号が成り立つ根拠は問題文中に示されている「令和4年の $x$ と $y$ の間には正の相関がある」の部分です。これにより共分散は正、すなわち $S_{x y} > 0$ となります。

以上より、「 $テ = 4$ 、 $ト = 0$ 」となります。

（３）

いわゆる二項検定に関する問題です。まずは題意を把握するところから取り組みます。問題文を読むと、太郎さんは「限られたサンプルからキャンペーンA、Bのどちらが良いと思ってる人が多いかを割り出す」ことについて慎重な態度であることが分かります。

要するに、太郎さんは1/2の確率でAとBのどちらが良いかを答える母集団を仮定して、アンケートの結果から導かれる結論が統計的に妥当かを判断したいということのようです。これをコイントスのモデルで検証する、というのが今回の問題のテーマになっています。（背景知識については末尾のPOINTも参考にしてください）

さて、表を読み取ると、35枚の硬貨のうち23枚以上が表となった割合は、 $2.4 + 0.9 + 0.5 + 0.4 + 0.1 = 4.3 (%)$ と求められるので、5 %を下回っています。したがって、“「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい” という仮説は誤っていると判断し、キャンペーンAの方がよいと思っている人が多いといえることが分かります。

したがって、「 $ナ = 4$ 、 $二 = 3$ 、 $ヌ = 0$ 、 $ネ = 0$ 」となります。

POINT

表の枚数が $n$ となった累積回数を棒グラフで表現したのが「実験結果」の図です。題意のような施行で得られる分布は「二項分布」に従っており、アンケート調査から統計的に有意な結果が得られたかどうかを、二項検定（Binomial Test）を利用することで検証する、というのが本問の筋書きです。

二項検定とは、「ある事象が偶然に起こったのか、それとも何か特別な要因が関与しているのか」を統計的に判断するための検定方法です。特に「成功と失敗」などの2種類の結果をもつ試行（ベルヌーイ試行）が複数回行われたときに、観測された結果が期待値と比べて統計的に有意な差があるかどうかを検定するために使います。二項検定は、製品の不良品検査や医薬品の有効性の検証など、様々な分野で利用される統計手法です。

この検定では有意水準 $α$ （統計的に「偶然とは考えにくい」と判断する基準のこと）として、 $α = 0.05$ （5 ％）が用いられることが多いです。今回の問題で太郎さんが5%未満かどうかに着目しているのは、この有意水準より大きいことを検証することを目的としているためです。

“「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しい” という仮説は、より専門的には「帰無仮説」と呼ばれます。これに対して “「キャンペーンAの方がよい」と回答する割合と「キャンペーンBの方がよい」と回答する割合は等しくない” という仮説を「対立仮説」と言います。

帰無仮説のもとでは、人々がAを選ぶ確率は $0.5$ なので、帰無仮説の下で「35人のうち23人以上がAを選ぶ確率」を計算すると、理論値としては（ $k$ を表の枚数として） $\begin{aligned} P (X \geq 23) & = \sum_{k = 23}^{35} P (X = k) \\ = \sum_{k = 23}^{35}_{35} C_{k} (0.5)^{35} \\ = 0.0447655 \dots \end{aligned}$ と計算できます。このことから、太郎さんが1000回のコイントスで求めた $0.043$ は理論値に近い値であることが分かります。検定で得られた確率が有意水準未満であれば帰無仮説を棄却するので、人々がAを選ぶ確率は $0.5$ より大きいことが結論されます。

それにしても35枚の硬貨を投げる実験を1000回手作業というのは、なかなかの苦行ですね…(笑)。

第１問と第２問前半に続いて、こちらも至ってシンプルな内容でした。問題文は長いですが、誘導がとても丁寧なので素早く解き切りたい問題です。

今年の問題は煩雑なデータの読み取りが無く、すべて問題文中にヒントが与えられた形式での出題となりました。受験生への配慮が行き届いた問題文だったと思います。

また、定義に立ち返らせる問題もあり、教育的な作りになっていると感じました。統計分野の理解が不十分な受験生は失点してしまったかもしれません。一方で難関大学の受験生同士ではほとんど差がつかなかったのではないかと思います。こういう易しめの1次試験の年は大抵ハイレベルでシビアな戦いになるので、むしろ気の毒な感じがします…。

2025年5月
月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

（１）

（２）

（３）

考え方・解答例

（１）

（２）

（３）

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル