2025年の共通テスト数学ⅠAの第3問を解説します。立体図形が登場しますが、落ち着いて解答したいところです。
6点 $A, B, C, D, E, F$ を頂点とし,三角形 $ABC$ と $DEF$,および四角形 $ABED, ACFD, BCFE$ を面とする五面体がある。ただし,直線 $AD$ と $BE$ は平行でないとする。
以下では,例えば,面 $ABC$ を含む平面を平面 $ABC$,面 $ABED$ を含む平面を平面 $ABED$,などということにする。
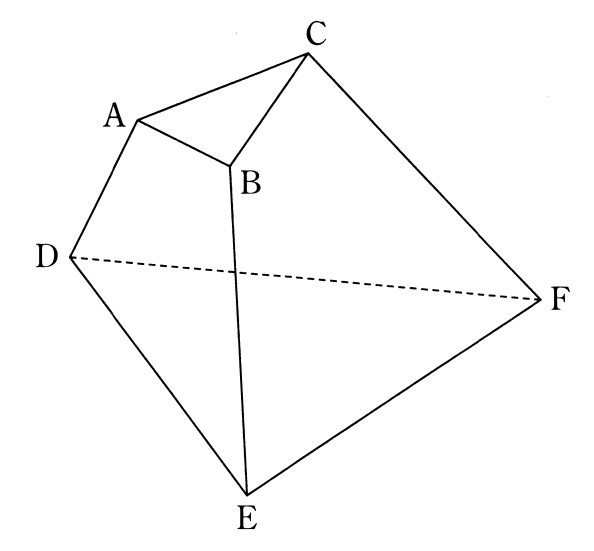 参考図
参考図
(1)
3直線 $AD, BE, CF$ は1点で交わる。これを証明しよう。
直線 $AD$ と $BE$ は平面 $ABED$ にあり,平行でないので1点で交わる。その交点を $P$ とする。
点 $P$ は直線 $AD$ 上にあり,直線 $AD$ は平面 $ABED$ と平面 $\boxed{\text{ア}}$ の交線であるから,点 $P$ は平面 $\boxed{\text{ア}}$ 上にあることがわかる。
また,点 $P$ は直線 $BE$ 上にあり,直線 $BE$ は平面 $ABED$ と平面 $\boxed{\text{イ}}$ との交線であるから,点 $P$ は平面 $\boxed{\text{イ}}$ 上にあることがわかる。
平面 $\boxed{\text{ア}}$ と平面 $\boxed{\text{イ}}$ との交線は直線 $CF$ であるから,点 $P$ は直線 $CF$ 上にもあることがわかる。したがって,3直線 $AD, BE, CF$ は点 $P$ で交わる。
$\boxed{\text{ア}}$,$\boxed{\text{イ}}$ の解答群(同じものを繰り返し選んでもよい。)
⓪ $ABC$
① $DEF$
② $ACFD$
③ $BCFE$
(2)
五面体において,面 $ABC$ は一辺の長さが $3$ の正三角形であり
\[
AD = 7, \quad BE = 11, \quad CF = 17, \quad DE = 9
\]であるとする。また,6点 $A, B, C, D, E, F$ はある一つの球面上にあるとし,その球面を $S$ とする。直線 $AD$ と $BE$ の交点を $P$ とする。
(ⅰ) 平面 $ABED$ と球面 $S$ が交わる部分は円であり,4点 $A, B, E, D$ はその円周上にある。このことから,三角形 $PAB$ と $PED$ は相似であることがわかり,その相似比は $1 : \boxed{\text{ウ}}$ である。したがって
\[
\boxed{\text{ウ}} \cdot PA = PB + \boxed{\text{エオ}}
\]\[
\boxed{\text{ウ}} \cdot PB = PA + \boxed{\text{カ}}
\]が成り立つ。よって
\[
PA = \boxed{\text{キ}}, \quad PB = \boxed{\text{ク}}
\]となる。
(ⅱ) 平面 $BCFE$ と球面 $S$ が交わる部分に着目すると,方べきの定理より
\[
PC = \boxed{\text{ケ}}
\]となる。したがって
\[
EF = \boxed{\text{コサ}}, \quad DF = \boxed{\text{シス}}
\]となる。
(ⅲ) $\angle ADE, \angle ADF, \angle EDF$ の大きさに着目すると,次の命題 (a), (b), (c) の真偽の組合せとして正しいものは $\boxed{\text{セ}}$ であることがわかる。
(a) 平面 $ABED$ と平面 $DEF$ は垂直である。
(b) 直線 $DE$ は平面 $ACFD$ に垂直である。
(c) 直線 $AC$ と直線 $DE$ は垂直である。
$\boxed{\text{セ}}$ の解答群
| ⓪ | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | |
|---|---|---|---|---|---|---|---|---|
| (a) | 真 | 真 | 真 | 真 | 偽 | 偽 | 偽 | 偽 |
| (b) | 真 | 真 | 偽 | 偽 | 真 | 真 | 偽 | 偽 |
| (c) | 真 | 偽 | 真 | 偽 | 真 | 偽 | 真 | 偽 |
考え方・解答例
(1)
直線 $AD$ は平面 $ABED$ と平面 $ACFD$ の交線なので、$\boxed{\text{ア}} = ACFD$、直線 $BE$ は平面 $ABED$ と平面 $BCFE$ の交線なので、$\boxed{\text{イ}} = BCFE$ と分かります。
よって「$\boxed{\text{ア}} = 2$、$\boxed{\text{イ}} = 3$」と分かります。
(2)
与えられた問題設定を図に起こすと下図のようになります。
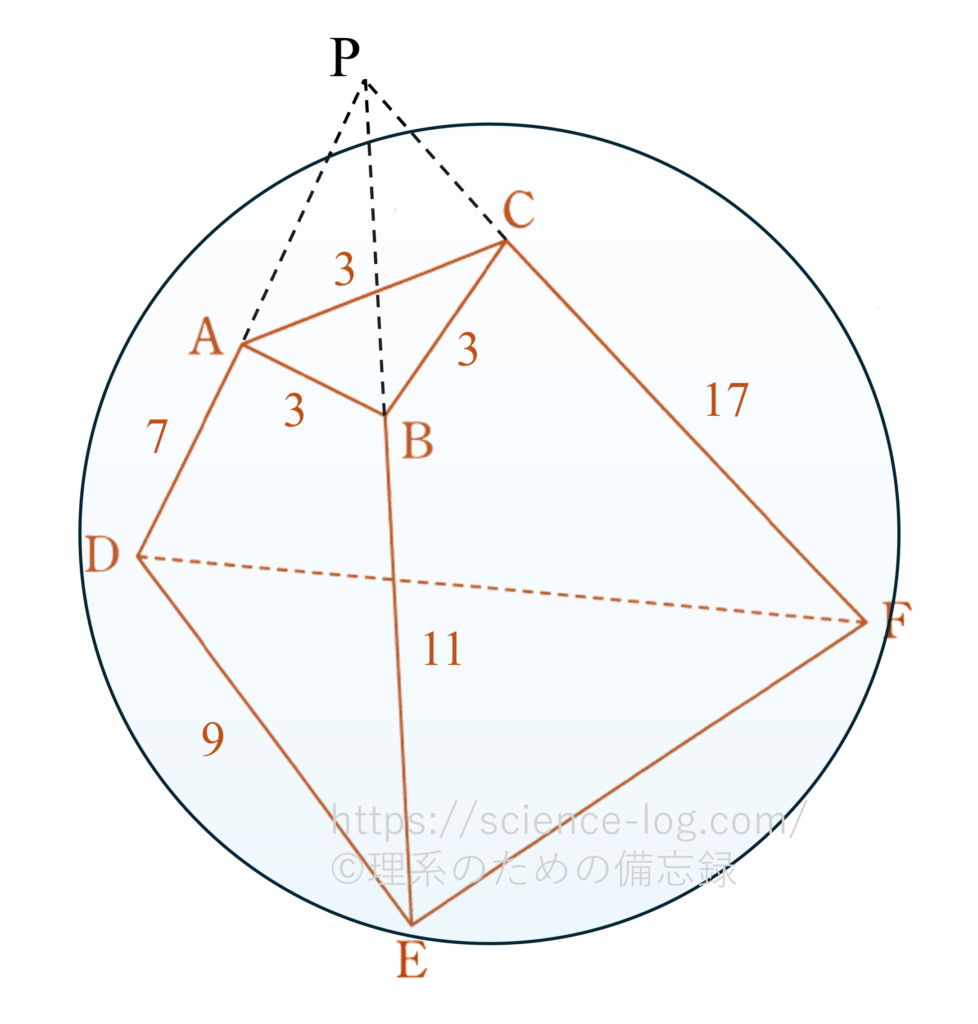
(ⅰ) 6点 $A, B, C, D, E, F$ はある一つの球面上に存在するので、そのうちの4点 $A, B, D, E$ はその球の断面となる円周上に存在しています。
$\triangle PAB$ と $\triangle PED$ は相似で、頂点$P$に対する底面はそれぞれ$AB$、$ED$ですから、相似比はそれらの長さの比に等しく、$AB:ED=3:9$すなわち、$$\triangle PAB : \triangle PED = 1:3$$となります。
したがって、$PE$、$PD$の長さはそれぞれ$PA$、$PB$の$3$倍と分かるので、関係式$$3 PA = PB + BE$$および$$3 PB = PA + AD$$を得ます。よって\begin{cases} 3 \cdot PA = PB + 11 \\ 3 \cdot PB = PA + 7 \end{cases}が成り立ちますから、連立して解いて\[
PA = 5, \quad PB = 4
\]となります。
よって、「$\boxed{\text{ウ}} = 3$、$\boxed{\text{エ}} = 1$、$\boxed{\text{オ}} = 1$、$\boxed{\text{カ}} = 7$、$\boxed{\text{キ}} = 5$、$\boxed{\text{ク}} = 4$」です。
(ⅱ) 平面 $ADFC$ についても同様に $\triangle PAC$ と $\triangle PFD$ の相似を考えると、$PA:PC=PF:PD$ が成り立つので、$$5:PC=PC+17 : 12$$ $$\therefore PC=3$$と求められます。これより、$PA:CA=PF:DF$ から、$$\therefore 5:3=20:DF$$ $$\therefore DF=12$$を得ます。
平面 $BCFE$ でも同様に $\triangle PBC$ と $\triangle PFE$ の相似を考えると、$PC:CB=PE:EF$ が成り立つので、$$3:3=15 : EF$$ $$\therefore EF=15$$と求められます。
よって、「$\boxed{\text{ケ}} = 3$、$\boxed{\text{コ}} = 1$、$\boxed{\text{サ}} = 5$、$\boxed{\text{シ}} = 1$、$\boxed{\text{ス}} = 2$」です。
上記では誘導を無視して方べきの定理を利用していませんが、誘導にしたがって「方べきの定理」から$$PB \cdot PE = PC \cdot PF$$のように立式して求めてもOKです。ミスなく計算できる方法を選びましょう。
(ⅲ) これまでの結果を図に起こしてみます。
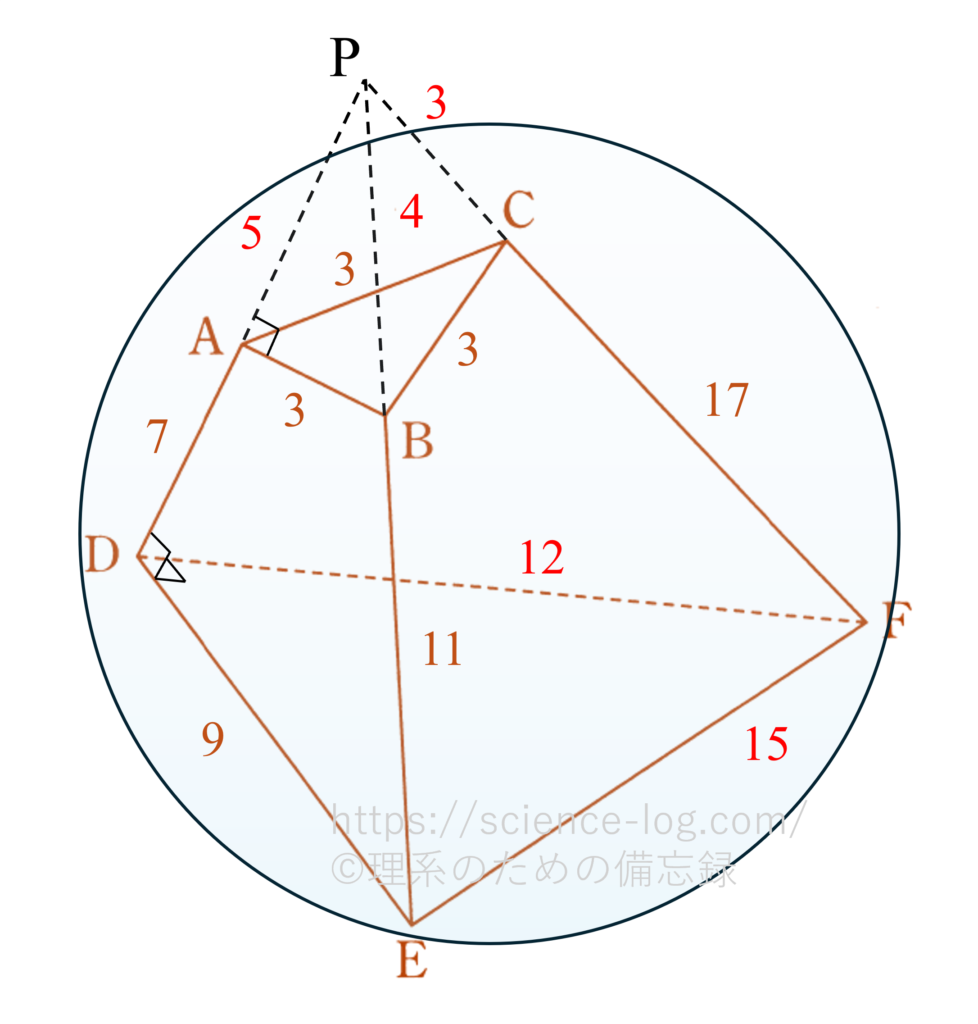
$\triangle PAB$ に着目すると、辺の長さが $3:4:5$ になっているので直角三角形だと分かります。よって、これと相似な $\triangle PDE$ も $\angle ADE = 90^{\circ}$ の直角三角形です。
また、$\triangle DEF$ について辺の長さが $3:4:5$ なので、これも直角三角形であり $\angle FDE = 90^{\circ}$ と分かります。
$\triangle PDF$ は $PD=FD=12$ の二等辺三角形で、$\angle ADF$ は直角ではありません。
以上のことから、$\angle ADF$ は直角でないので「(a) 平面 $ABED$ と平面 $DEF$ は垂直である。」は偽です。
また、$\angle ADE$ と $\angle EDF$ が直角なので、平面 $ACFD$ と直線 $DE$ は垂直の関係にあります。したがって、平面 $ACFD$ 上に存在する直線 $AC$ と直線 $DE$ も垂直です。
よって、「(b) 直線 $DE$ は平面 $ACFD$ に垂直である。」および「(c) 直線 $AC$ と直線 $DE$ は垂直である。」は真です。
よって、「$\boxed{\text{セ}} = 4$」と分かります。
立体図形が登場して焦った受験生が多かったかもしれませんが、平面ごとに考えれば単純な相似・円周上の多角形の問題にすぎません。
線分の長さが正しく計算できていれば最後の (ⅲ) も問題なく解答できると思います。特に、今回は辺の長さが $3:4:5$ となる三角形があることに気が付けば解答は容易です。ここを間違えた方は「直線と直線が垂直になる条件」、「直線と平面が垂直になる条件」、「平面と平面が垂直になる条件」をよく確認しておきましょう。
