英国の名門大学であるケンブリッジ大学とウォーリック大学の入試に使われている数学のテスト「STEP」から、昨年の問題を取り上げてみます。イギリスの大学受験生が解いている問題を眺めるのも勉強になる・・・かもしれません。
「Sixth Term Examination Paper」(通称 STEP) は数学の入学試験問題で、11問もしくは12問の問題から6つの問題を選択して解答する形式の試験です。STEPには1、2、3の3種類があり、この順に難度が上がります。
イギリスではSTEPの他に「Mathematics Admissions Test」(通称 MAT) や「Test of Mathematics for University Admission」(通称 TMUA) などの共通数学試験があります。STEPがすべて記述式なのに対してMATでは一部、TMUAでは全てがマーク式の問題になっています。問題の難しさは、おおよそ
STEP3>STEP2>STEP1≈MAT>TMUA
という序列になっており、STEP2,3になると日本の高校数学レベルを超えた内容まで出題されます。
今回は2019年のSTEP1から第1問をご紹介します。
《問題》
A straight line passes through the fixed point $(1, k)$ and has gradient $-\tan \theta$, where $k > 0$ and $0 < \theta < \dfrac{1}{2}\pi$. Find, in terms of $\theta$ and $k$, the coordinates of the points $X$ and $Y$ where the line meets the $x$-axis and the $y$-axis respectively.
(i)
Find an expression for the area $A$ of triangle $OXY$ in terms of $k$ and $\theta$. (The point $O$ is the origin.)
You are given that, as $\theta$ varies, $A$ has a minimum value. Find an expression in terms of $k$ for this minimum value.
(ii)
Show that the length $L$ of the perimeter of triangle $OXY$ is given by $$\small L = 1+\tan\theta + \sec\theta + k(1 + \cot \theta + \operatorname{cosec}\theta).$$
You are given that, as $\theta$ varies, $L$ has a minimum value. Show that this minimum value occurs when $\theta = \alpha$ where $$\small \dfrac{1-\cos \alpha}{1-\sin \alpha} = k.$$ Find and simplify an expression for the minimum value of $L$ in terms of $\alpha$.
(STEP2019 MATHⅠ §A p1)
» 和訳はこちら
ある直線は定点 $(1, k)$ を通り、勾配が $-\tan \theta$ であり、$k > 0$ と $0 < \theta < \dfrac{1}{2}\pi$ を満たしている。$\theta$ と $k$ を用いて、この直線と $x$ 軸と $y$ 軸との交点 $X$ および $Y$ の座標を求めよ。
(i)
三角形 $OXY$ の面積 $A$ を $k$ と $\theta$ で表せ。(ただし点 $O$ は原点とする)
$\theta$ が変化するとき、$A$ は最小値を持つ。その最小値を $k$ で表せ。
(ii)
三角形 $OXY$ の外周の長さ$L$が、$$\small L = 1+\tan\theta + \sec\theta + k(1 + \cot\theta + \operatorname{cosec}\theta)$$ で与えられることを示せ。
$\theta$ が変化するとき、$L$ は最小値を持つ。この最小値は$$\small \dfrac{1-\cos \alpha}{1-\sin \alpha} = k$$を満たす角 $\theta = \alpha$ のときにとることを示せ。$L$ の最小値を $\alpha$ を用いて簡単な式で表せ。
» 閉じる
《考え方》
問題の中身は至って普通です。まずは直線の方程式を求めましょう。
解答例
the coordinates of the points $X$ and $Y$
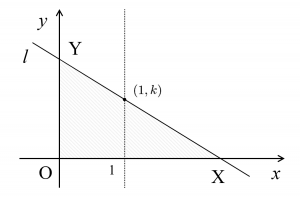
定点 $(1, k)$ を通り、勾配が $-\tan \theta$ であるような直線 $l$ の方程式は$$l:y=-\tan \theta \cdot x+k+\tan \theta$$となる。よって$x$切片および$y$切片は $x=\dfrac{k}{\tan \theta}+1$、$y=k+\tan \theta$ となるから、点 $X$ および $Y$ の座標は$$\color{red}{X\left(\dfrac{k}{\tan \theta}+1,0\right),\,Y\left(0,k+\tan \theta\right)}$$と求められる。
(ⅰ)
三角形 $OXY$ の面積 $A$ は$$\begin{align} A&=\dfrac{1}{2} \times OX \times OY \\ &=\dfrac{1}{2}\left(\dfrac{k}{\tan \theta}+1\right)\left(k+\tan \theta\right) \\ &=\color{red}{\dfrac{1}{2}\tan \theta + \dfrac{k^2}{2\tan \theta}+k} \end{align}$$
いま、$\tan \theta>0$ であるから相加・相乗平均の不等式より、$$\begin{align} A &=\dfrac{1}{2}\tan \theta + \dfrac{k^2}{2\tan \theta}+k \\ &= \dfrac{1}{2}\left(\tan \theta + \dfrac{k^2}{\tan \theta}\right)+k \\ & \geqq \dfrac{1}{2} \cdot 2\sqrt{\tan \theta \cdot \dfrac{k^2}{\tan \theta}}+k \\ & \geqq \color{red}{2k} \end{align}$$等号が成立するのは$\tan \theta = \dfrac{k^2}{\tan \theta}$、すなわち、$$\tan \theta =k$$のときである。$0 < \theta < \dfrac{1}{2}\pi$ であるから $\tan \theta$ は任意の正の実数値をとる。よって任意の $k\,(>0)$ に対して $\tan \theta =k$ となる $\theta$ が存在するから、最小値 $2k$ は必ず存在する。
(ⅱ)
三角形 $OXY$ の外周の長さ$L$が$$\small L = 1+\tan\theta + \dfrac{1}{\cos\theta} + k\left(1 + \dfrac{1}{\tan\theta} + \dfrac{1}{\sin\theta}\right)$$で与えられることを示す。
$$\small \begin{cases} OX=\dfrac{k}{\tan \theta}+1 \\ OY=k+\tan \theta \\ \begin{align} XY&=\sqrt{OX^2+OY^2} \\ &=\sqrt{\left(\dfrac{k}{\tan \theta}+1\right)^2+\left(k+\tan \theta\right)^2} \\ &=\sqrt{k^2\left(\dfrac{1}{\tan ^2\theta}+1\right)+2k\left(\dfrac{1}{\tan \theta}+\tan \theta\right)+\left(\tan^2 \theta+1\right)} \\ &=\sqrt{\dfrac{k^2}{\sin^2\theta}+\dfrac{2k}{\sin\theta\cos\theta}+\dfrac{1}{\cos^2\theta}} \\ &=\sqrt{\left(\dfrac{k}{\sin \theta}+\dfrac{1}{\cos\theta}\right)^2}\\ &=\dfrac{k}{\sin \theta}+\dfrac{1}{\cos\theta} \end{align} \end{cases}$$より、三角形 $OXY$ の外周の長さ $L$ $(=OX+OY+XY)$ は$$\small L = 1+\tan\theta + \dfrac{1}{\cos\theta} + k\left(1 + \dfrac{1}{\tan\theta} + \dfrac{1}{\sin\theta}\right)$$で与えられる。
また、$L$ を $\theta$ の関数 $L(\theta)$ と見なすと、$$\small \begin{align} L'(\theta)&=\dfrac{1}{\cos^2\theta}+\dfrac{\sin\theta}{\cos^2\theta}-\dfrac{k}{\sin^2\theta}-\dfrac{k\cos\theta}{\sin^2\theta} \\ &=\dfrac{\sin^2\theta+\sin^3\theta-k(\cos^2\theta+\cos^3\theta)}{\sin^2\theta\cos^2\theta}\end{align}$$となる。
よって関数 $L(\theta)$ の増減は$$\small \sin^2\theta+\sin^3\theta-k(\cos^2\theta+\cos^3\theta)=0$$を満たす$\theta$の前後で変化する。この等式を整理すると、$$\therefore \small \dfrac{\sin^2\theta+\sin^3\theta}{\cos^2\theta+\cos^3\theta}=k$$ $$\therefore \small \dfrac{\sin^2\theta(1+\sin\theta)}{\cos^2\theta(1+\cos\theta)}=k$$ $$\therefore \small \dfrac{(1-\cos^2\theta)(1+\sin\theta)}{(1-\sin^2\theta)(1+\cos\theta)}=k$$ $$\therefore \small \dfrac{1-\cos\theta}{1-\sin\theta}=k$$となる。ここで、角 $\theta = \alpha$ はこれを満たすから、$$\small \dfrac{1-\cos \alpha}{1-\sin \alpha} = k$$を満たす角 $\theta = \alpha$ のときに$L$ は最小値をとる。
よって最小値は$$\small \begin{align} & \quad 1+\tan\alpha + \dfrac{1}{\cos\alpha} + \dfrac{1-\cos\alpha}{1-\sin\alpha}\left(1 + \dfrac{1}{\tan\alpha} + \dfrac{1}{\sin\alpha}\right) \\ &=1+\dfrac{\sin\alpha+1}{\cos\alpha} + \dfrac{1-\cos\alpha}{1-\sin\alpha}\left(1 + \dfrac{\cos\alpha+1}{\sin\alpha}\right) \\ &=1+\dfrac{\sin\alpha+1}{\cos\alpha} + \dfrac{1-\cos\alpha}{1-\sin\alpha}+\dfrac{1-\cos^2\alpha}{\sin\alpha(1-\sin\alpha)} \\ &=1+\dfrac{(1-\sin^2\alpha)+\cos\alpha(1-\cos\alpha)}{\cos\alpha(1-\sin\alpha)}+\dfrac{\sin\alpha}{1-\sin\alpha} \\ &=1+\dfrac{1}{1-\sin\alpha}+\dfrac{\sin\alpha}{1-\sin\alpha} \\ &=\color{red}{\dfrac{2}{1-\sin\alpha}}\end{align}$$と求められる。
(コメント)
日本の入試と比べてどうでしょうか? 本問に関してはごく普通の問題という感じでしたね。(ⅰ)について、微分を用いても$A$の最小値を求めることができます。ですが相加相乗平均の不等式を使う方が簡単だと思います。(ⅱ)では特に増減表を書いていませんが、$L(\theta)$ が最小値をとる($L'(\theta)$ が一度だけ負→正と符号が変化する)ことは $\small \dfrac{\sin^2\theta+\sin^3\theta}{\cos^2\theta+\cos^3\theta}$ が $\small 0 < \theta < \dfrac{\pi}{2}$ の範囲で単調増加することから導かれます。
