コラッツ予想とコラッツ数列について

最近、日本のIT企業「株式会社音圧爆上げくん」が数学の未解決問題である「コラッツ予想」の解決に対して、賞金1億2000万円を懸けたというニュースが話題になりました（詳細のPDFファイルはこちら）。今回はこのコラッツ予想について紹介したいと思います。

 コラッツ予想とは？

コラッツ予想そのものは小学生でも理解できる簡単なものです。

具体的に考えてみましょう。例えば$n$を$5$としたとき、上記の操作を繰り返すと

$5, 16, 8, 4, 2, 1$

という数列が得られます。$5$は奇数なので$3$をかけて$1$を足すと$16$になり、$16$は偶数なので$2$で割ると$8$になり、･･･という操作を続けていくと、この数字の並びが出てきます。

実はこの「コラッツ予想」、ドイツの数学者ローター･コラッツが問題を提示したのは1937年と今から80年以上も前なのですが、現在でも完全には証明できていない「未解決問題」なのです。「コラッツ予想」は「コラッツ問題」とも呼ばれ、このような数列の作り方から「3n+1問題」と呼ばれることもあります。

※今回は深く立ち入りませんが、「3n+1」の部分を改変して「3n-1」や「3n+3」、「n+1」などにしても面白い考察ができます。

※この問題に取り組んだ研究者の名を冠して「角谷問題」と呼ばれることもあります。

この操作によって得られる数列は「コラッツ数列」と呼ばれ、盛んに研究されています。因みに、現在は$2^{68}$以下の数についてコラッツ予想が正しいことがコンピュータによって確かめられており、多くの数学者はコラッツ予想が正しいと考えています。しかし、このことから$2^{68}$より大きな数について何か言える訳ではなく、コラッツ予想が未解決問題であることに変わりはありません。

 コラッツ数列を求める

$2$～$20$までの範囲でコラッツ数列を求めると、以下のようになります。

・2→1 (2項)
・3→10→5→16→8→4→2→1 (8項)
・4→2→1 (3項)
・5→16→8→4→2→1 (6項)
・6→3→10→5→16→8→4→2→1 (9項)
・7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1 (17項)
・8→4→2→1 (4項)
・9→28→14→7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1 (20項)
・10→5→16→8→4→2→1 (7項)
・11→34→17→52→26→13→40→20→10→5→16→8→4→2→1 (15項)
・12→6→3→10→5→16→8→4→2→1 (10項)
・13→40→20→10→5→16→8→4→2→1 (10項)
・14→7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1 (18項)
・15→46→23→70→35→106→53→160→80→40→20→10→5→16→8→4→2→1 (18項)
・16→8→4→2→1 (5項)
・17→52→26→13→40→20→10→5→16→8→4→2→1 (13項)
・18→9→28→14→7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1 (21項)
・19→58→29→88→44→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1 (21項)
・20→10→5→16→8→4→2→1 (8項)

どの整数$n$から始めても最終的には$1$になっている行き着く様子が分かります。数列の長さは整数$n$の値によって区々まちまちですね。

原理的には手計算で求めることができますが、それなりに骨が折れます。ここから先はコンピュータ君にお任せしてしまいましょう。$n=1000$ までのコラッツ数列を以下のページに掲載しておきました。Pythonのサンプルコードも載せておきますので、参考までに。

「n=1000までのコラッツ数列一覧」
（※データ量が大きいので読み込みに時間が掛かるかもしれません）

def Collatz(n):
    length = 1;  numlist = []
    while n != 1: # 1になるまで繰り返す
        numlist.append(n)
        if n & 1: # ビット積
            n = 3 * n + 1
        else:
            n = n // 2
        length += 1
    numlist.append(n)
    return length, numlist

maxnum = 101
length_list = []

for i in range(2, maxnum):
    length, numlist = Collatz(i)
    print(length, numlist)

 コラッツ数列の長さと最大値

ここでコラッツ数列の長さ（数列の項数）に注目し、何か規則性がないか探ってみます。以下に $2 \leqq n \leqq 100$ の範囲で調べたコラッツ数列の長さの散布図を示します。

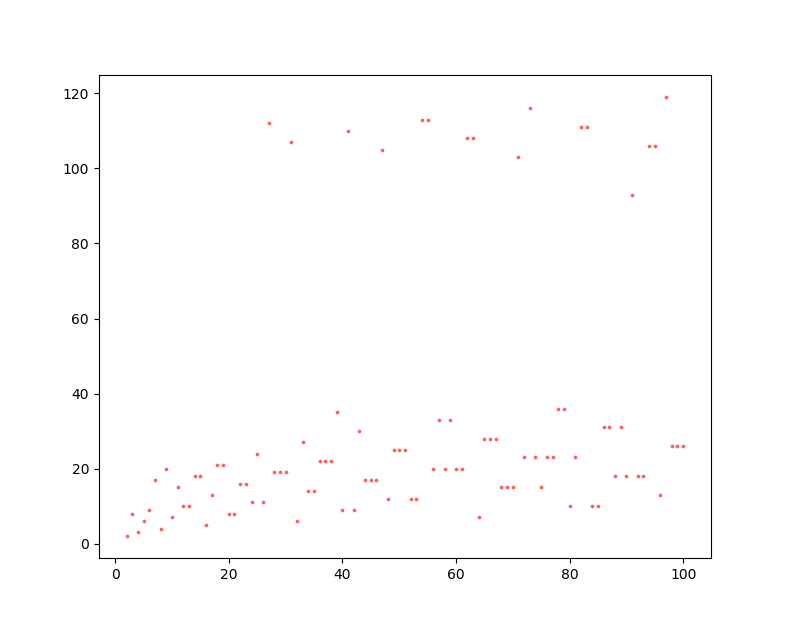図1．コラッツ数列の長さ（100まで）

何となく2層に分かれているような印象を受けますね。$2 \leqq n \leqq 1000$ の範囲で$n$の偶数/奇数の別で色分けしてみると下のようになります。

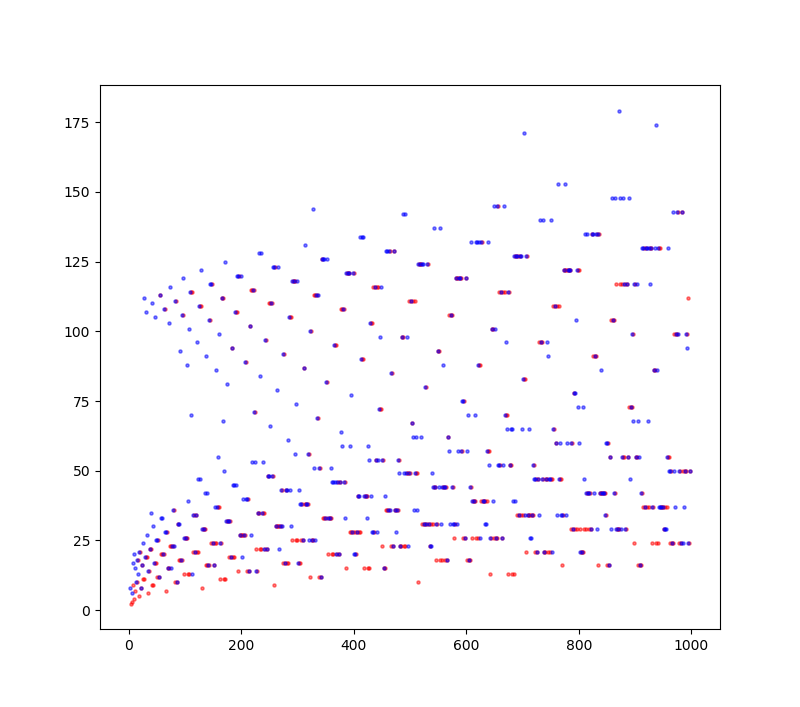図2．コラッツ数列の長さ（1000まで）

よりはっきりと層に分かれていることは分かりますが、綺麗に色分けできていません。残念ながらこれはヒントにならなさそうです。

もう少し先まで調べてみましょう。$2 \leqq n \leqq 10000$ の範囲でプロットすると同じような模様が見えてきます。

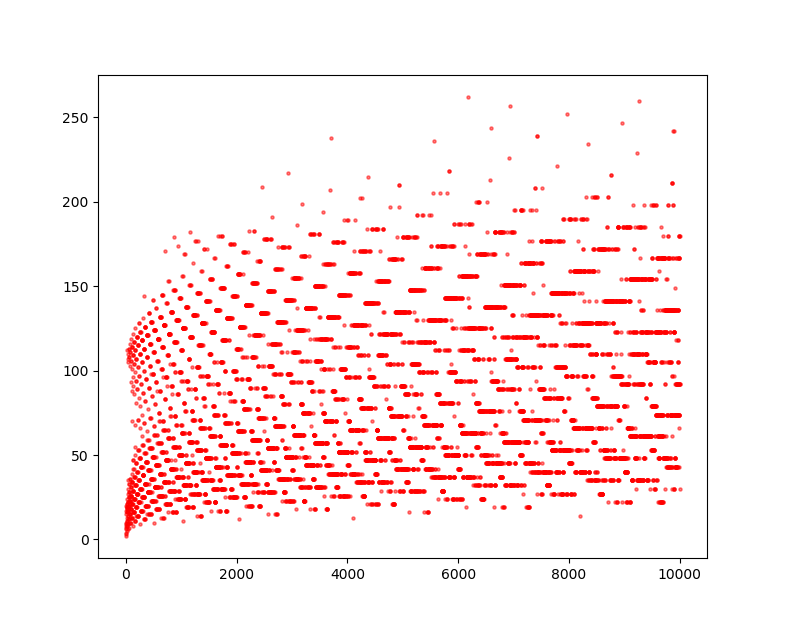図3．コラッツ数列の長さ（10000まで）

続いてコラッツ数列の最大値について調べてみます。以下に $2 \leqq n \leqq 100$ の範囲で調べたコラッツ数列の最大値の散布図を示します。

図4．コラッツ数列の最大値（100まで）

点列が完全に2層に分かれていますね。多くの$n$では縦軸の値が$1000$未満の小さい値となりますが、上の方にある点の値はすべて$9232$です。その次に大きな値は$808$と、かなり差が開いています。

この傾向は$n$の範囲を大きくしても変わりません。

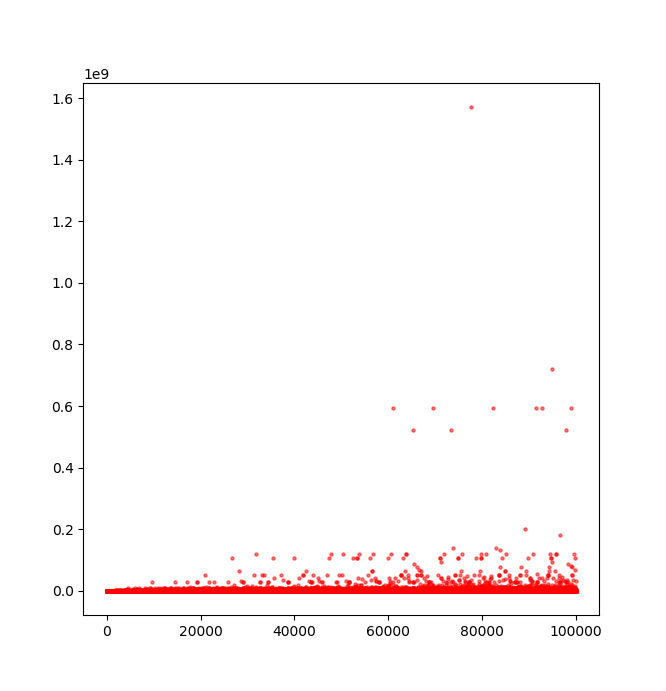図5．コラッツ数列の最大値（100000まで）

これは $2 \leqq n \leqq 10^5$ の範囲で調べたコラッツ数列の最大値の散布図ですが、同様にプロットが非常に離散的になっています（縦軸は$10^9$オーダー）。

縦軸の範囲を狭めると、もう少し綺麗なプロットになります。以下は $2 \leqq n \leqq 10^4$ の範囲で縦軸の最大値を$10^5$としたときの図です。

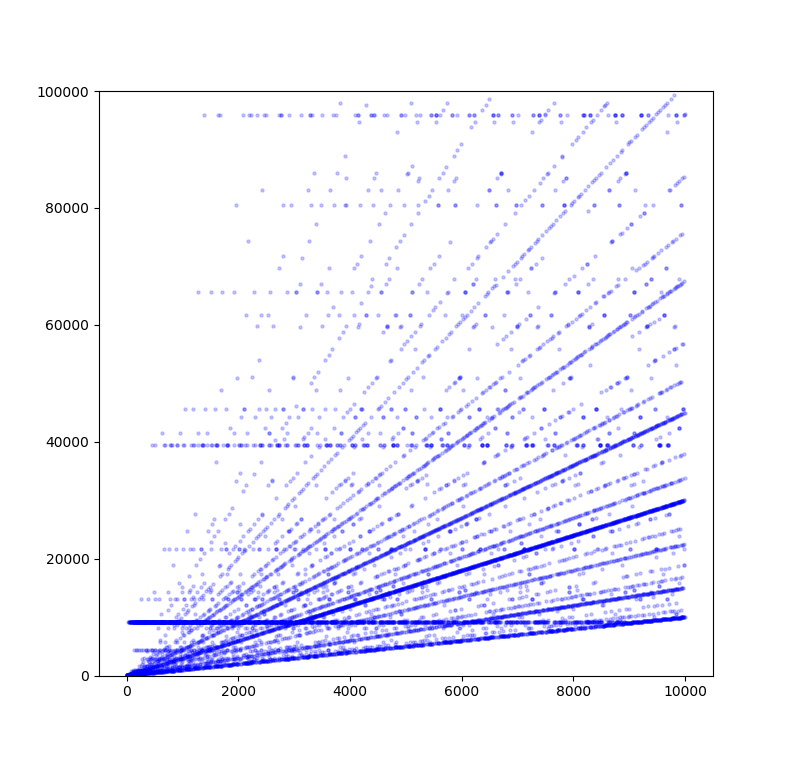図6．コラッツ数列の最大値（10000まで）

直線が浮かび上がって見えます。例えば、横軸に平行な最も濃い直線は高さ$9232$の直線です。この値は先ほども出てきましたね。

import matplotlib.pyplot as plt

maxnum = 10001
num_list = [i for i in range(2,maxnum)]
maxval_list = []

for i in range(2, maxnum):
    length, tmp_list = Collatz(i)
    maxval_list.append(max(tmp_list))

ax = plt.figure(figsize=(4,4), dpi=100).add_subplot(111)
ax.scatter(num_list, maxval_list, c="b", s=5.0, alpha=0.2)
plt.ylim(0, 10**5)  # 縦軸の上限を指定
plt.show()

こうしたグラフが得られるのはコラッツ数列の特徴ですが、これらから具体的な規則性を導くのは難しそうです。

 コラッツ数列のグラフ

ある一つの$n$の値に対して得られるコラッツ数列のグラフは次のようになります。

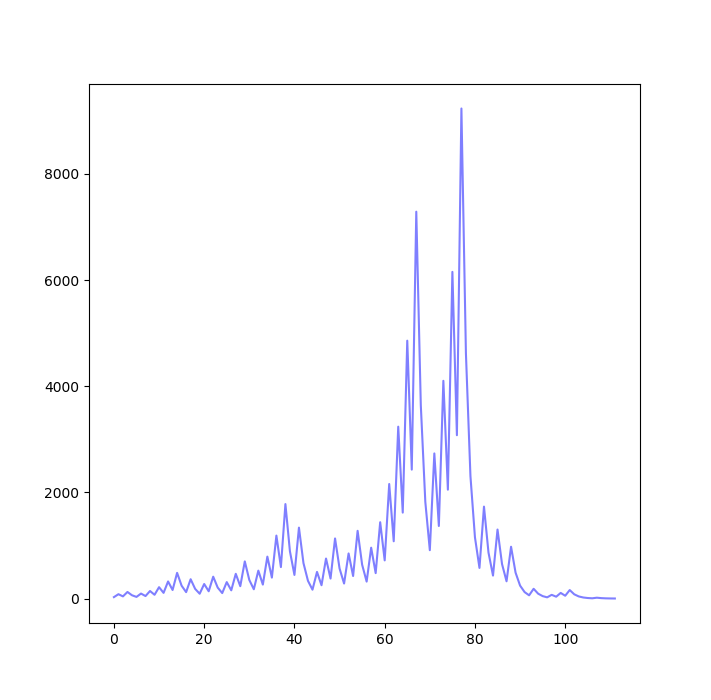図7．コラッツ数列の推移
（$n=27$ のとき）

これは $n=27$ の場合について横軸を項番号、縦軸を項の値としてコラッツ数列の折れ線グラフをプロットしたものです。

$2 \leqq n \leqq 30$ の場合のコラッツ数列を重ねてプロットすると次のようになります。$n=0$ を紫色、$n=30$ を黄色として、$n$の大きさに応じて折れ線の色をグラデーションで表示しています。

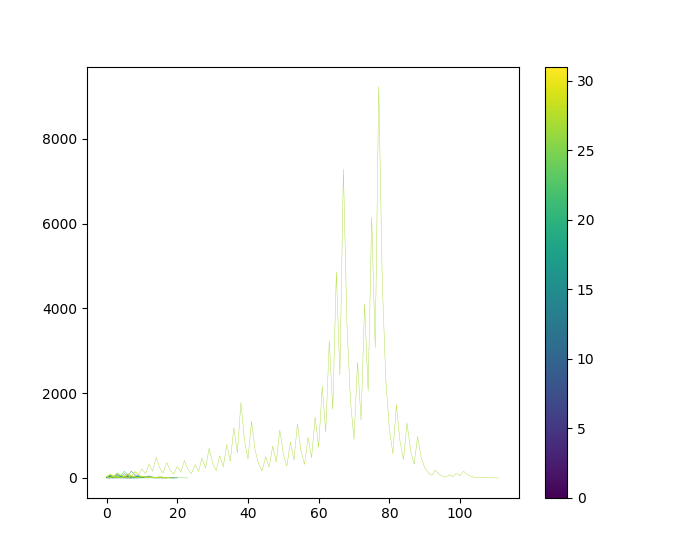図8．コラッツ数列の推移
（$n=2$～$30$）

$n=27$ のときに突出して項数が多い（コラッツ数列が長い）ことが一目瞭然ですね。$2$～$100$では次のようになります。

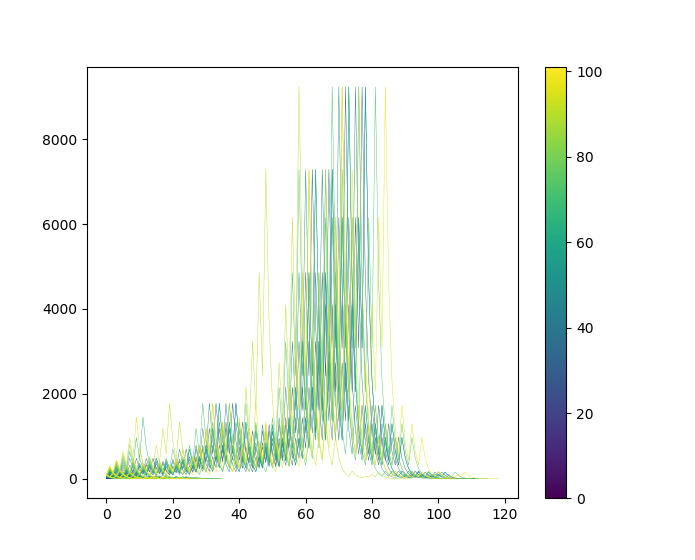図9．コラッツ数列の推移
（$n=2$～$100$）

コラッツ数列の最大値が $9232$ に到達している$n$が幾つか存在することが見て取れます。横軸に平行なラインがうっすら見えるような気もします。なお、この図9の折れ線の終点の横軸の値は図1の縦軸の値に相当しています。横軸$40$～$80$の辺りに折れ線の終点が無いことは図1からも確かめられます。

$n=1000$ までをプロットしてみると次のようになります。小さい$n$（色の濃い折れ線）では$9232$のラインで堰き止められている・・・・・・・・・様子がよく分かります。

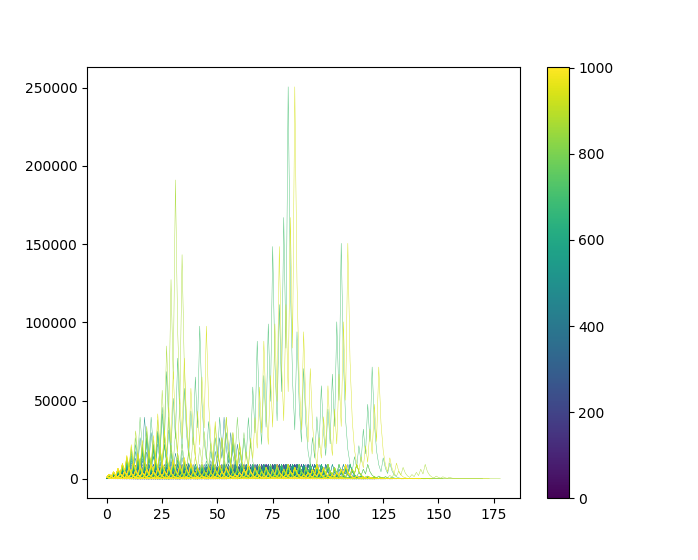図10．コラッツ数列の推移
（$n=2$～$1000$）

ついでに $n=2$～$10000$ についても同様のプロットも載せておきます。ごちゃごちゃしていて何だかよく分かりませんが…。

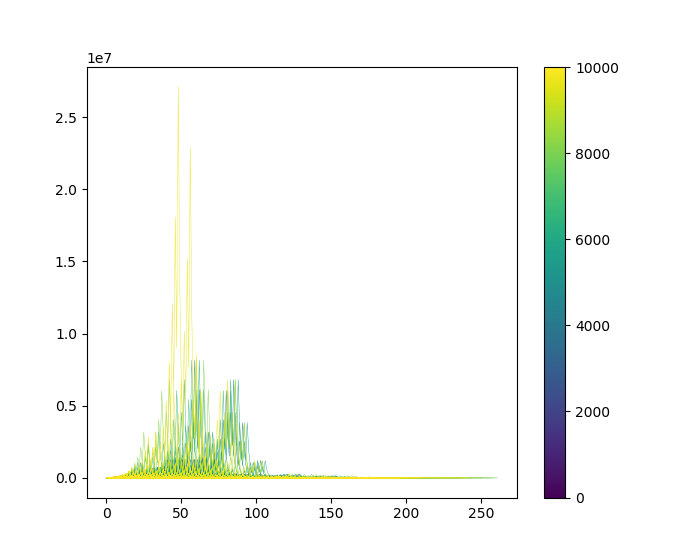図11．コラッツ数列の推移
（$n=2$～$10^4$）

from matplotlib import pyplot as plt
from matplotlib import colors
from matplotlib.cm import ScalarMappable

def Collatz(n):
    length = 1;  numlist = []
    while n != 1: # 1になるまで繰り返す
        numlist.append(n)
        if n & 1: # ビット積
            n = 3 * n + 1
        else:
            n = n // 2
        length += 1
    numlist.append(n)
    return length, numlist

maxnum = 101
fig = plt.figure(figsize=(4,4), dpi=100)
ax = fig.add_subplot(111)
cn = colors.Normalize(0, maxnum)  # 色調の規格化

for i in range(2,maxnum):
    length, numlist = Collatz(i)
    num_list = [i for i in range(0,length)]
    ax.plot(num_list, numlist, linewidth=0.3, alpha=1, color=plt.cm.viridis(cn(i)))

mappable = ScalarMappable(cmap='viridis', norm=cn) #カラーバー用
fig.colorbar(mappable)
plt.show()

 入試にも登場するコラッツ予想

コラッツ予想は未解決問題ですが、実は入試に時々登場しています。例えば、2011年度のセンター試験数学Ⅱ･Ｂ第6問では題材としてコラッツ予想が扱われています。当時の受験生はまさか未解決問題が背景にあるとは思わなかったでしょう（勿論、問題自体は解答可能です）。（１）までの問題文を抜粋します。

（出典：2011年度センター試験数学Ⅱ･Ｂ第6問）

数列を求める操作自体は簡単なので、ここまで読み進めて来た方にとっては簡単だと思います。数列はそれぞれ

6→3→10→5→16→8→4→2→1

11→34→17→52→26→13→40→20→10→5→16→8→4→2→1

となるので、答えは順に8, 14です。

コラッツ問題は設定が分かりやすいため、高校入試でも盛んに取り上げられています。最近だと、愛知県の公立高校入試（2020年,全日制課程B）、都立西高校（2020年, 自校作成問題）などで出題例があります。

（出典：2020年 愛知県公立高校 全日制B）

（出典：2020年 都立西高校）

他にも出題多数なのでトピックとして押さえておくと、いざという時に慌てずに済むかもしれません。中学受験でも時折登場することがあり、今年（2021年）の慶應義塾中等部の試験では「12回の操作で$1$になる整数の個数」を求めさせる問題が出題されています。（答えは17, 96, 104, 106, 113, 640, 672, 680, 682, 4096の10個です）