今年の北大理系数学では格子点を題材とする整数問題が出題されました。また、複素平面が2年連続で出題されませんでした。
《問題》
座標平面上の2点 $\left(\dfrac{1}{16}, 0\right)$、$\left(0, \dfrac{1}{9}\right)$ を通る直線 $l$ を考える。
(1)$l$ 上にある格子点の座標をすべて求めよ。ただし、格子点とはその点の$x$座標と$y$座標がともに整数であるような点のことである。
(2)$l$ 上の格子点のうち、原点との距離が最小となる点をAとする。また、$l$ 上のA以外の格子点のうち、原点との距離が最小となる点をBとする。さらに、Aの$x$座標とBの$y$座標をそれぞれ$x$座標と$y$座標とする点をCとする。三角形ABCの内部および周上にある格子点の個数を求めよ。
(北海道大学2020年 前期理系第2問)
《考え方》
2点 $\left(a, 0\right)$、$\left(0, b\right)$ を通る直線の方程式は$$\dfrac{x}{a}+\dfrac{y}{b}=1$$で与えられます。与えられている2点は軸の切片になっているので直線$l$はすぐ求められると思います。$l$ 上にある格子点の座標を表現するためにはパラメータを持ち出す必要があります。(2)も落ち着いて考えれば易しい問題です。
● ● ●
解答例
(1)
2点 $\left(\dfrac{1}{16}, 0\right)$、$\left(0, \dfrac{1}{9}\right)$ を通る直線 $l$ の方程式は$$16x+9y=1 \quad \cdots①$$で与えられる。$(x,y)=(4,-7)$ は方程式$①$の解の一つであるから、$$16 \cdot 4 + 9 \cdot (-7)=1 \quad \cdots②$$であり、$①-②$ より$$16(x-4)+9(y+7)=0$$を得る。これより整数$m$を用いると一般解は$$\begin{cases}x=9m+4 \\ y=-16m-7\end{cases}$$と表せるので、求める格子点は$$(x,y)=\color{red}{(9m+4,-16m-7)}$$となる。ただし$m$は整数である。
(2)
$m=-2$ のとき $(-14,25)$ で原点との距離は$\sqrt{821}$、
$m=-1$ のとき $(-5,9)$ で原点との距離は$\sqrt{106}$、
$m=0$ のとき $(4,-7)$ で原点との距離は$\sqrt{65}$、
$m=1$ のとき $(13,-23)$ で原点との距離は$\sqrt{698}$となる。
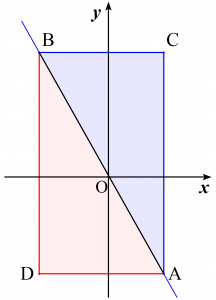
これより、点A$(4,-7)$、点B$(-5,9)$、点C$(4,9)$となる。
さらにここで点D$(-5,-7)$をとると、四角形ACBDの内部および周上にある格子点の個数は$$\begin{align}&\{4-(-5)+1\}\times\{9-(-7)+1\} \\ =&\,10 \times 17 \\ =&\,170 \end{align}$$と求められる。このうち対角線AB上に存在するのは$(4,-7)$、$(-5,9)$の2点のみであるから、三角形ABCの内部および周上にある格子点の個数は$$(170-2) \div 2 + 2=\color{red}{86}$$と計算できる。
(コメント)
完答しなければならないレベルの大問です。(1)は一次不定方程式の典型的な問題です。(2)もかなり易しい問題です。解答例では少しスマートに個数を求めましたが、数え上げも十分に可能な設定の問題でした。
△ABC内部の格子点と△ABD内部の格子点の個数が等しいことに着目すると煩雑な数え上げ作業が不要になります(下図参照)。このとき、対角線AB上の格子点を重複して数えてしまわないように気を付けましょう。