多項式の剰余の問題です。modの力で解決しましょう。
《問題》
$n$ を整数とするとき、$n^2+n+2$ は$5$で割り切れないことを証明しなさい.
(千葉大学2017 先進科学Ⅰ第5問)
《考え方》
$\text{mod} \ 5$ で考えれば瞬殺です。$n^2+n+2$ を$N$と置きます。
$n \equiv 0 \pmod{5}$ のとき、$N \equiv 2 \pmod{5}$、
$n \equiv 1 \pmod{5}$ のとき、$N \equiv 4 \pmod{5}$、
$n \equiv 2 \pmod{5}$ のとき、$N \equiv 3 \pmod{5}$、
$n \equiv 3 \pmod{5}$ のとき、$N \equiv 4 \pmod{5}$、
$n \equiv 4 \pmod{5}$ のとき、$N \equiv 2 \pmod{5}$
となるので、任意の整数$n$について $n^2+n+2$ は$5$で割り切れません。
(コメント)
合同式は便利ですが解答が非常に素っ気無いものになってしまうのが玉に瑕ですね・・・。
・・・ということで少し一般化してみましょう。
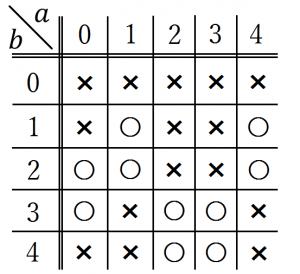
$N’=n^2+an+b$ と置くとき、$N’$が任意の整数$n$について$5$で割り切れないような$0$以上$5$以下の整数の組$(a,b)$を調べますと、以下のようになります。
表は $\text{mod} \ 5$ で示しており、「✖」は$N’$がある$n$について$5$で割り切れてしまうとき($5$の倍数となるような$n$が存在するとき)、「◯」は$N’$が任意の整数$n$について$5$で割り切れないときを表しています。本問は $(a,b)=(1,2)$ のときを問題にしたものです。
この表によれば「$n^2+2n+3$ は$5$で割り切れないことを証明しなさい」とか「$n^2+3n+4$ は$5$で割り切れないことを証明しなさい」といった類題が作れることが分かりますね。
本問の場合は1文字の2次式ですが、数学オリンピックなどでは2文字の3次式とか4次式とかが出てきますので、本問よりも遥かにハイレベルの出題となります。
なお解法としては、解答例では剰余類を利用していますが、もちろん $n=5k+1$、$n=5k+2$、・・・ のように順次代入して計算してもOKです。ただし記述量を考えると $\text{mod} \ 5$ で解答した方がかなり有利だと思います。