千葉大は良問を多く出題しており今年の問題も例外ではありません。難関大志望者であれば step up のための演習に持って来いです。合同式の話題です。
《問題》
$a,b$を正の整数とするとき、次を証明せよ。
（１）$a^3-a$は$3$の倍数である。
（２）$a-b$が$3$の倍数ならば、$a^3-b^3$は$9$の倍数である。
（３）$a^3-b^3$は、$3$の倍数ならば$9$の倍数である。
（千葉大学2017 前期第３問）
《考え方》
$3$を法とする合同式の出番です。（合同式についてはコチラをご参照ください）
（１）は誰でも知っている通り、$3$つの隣接する整数には必ず$3$の倍数が含まれるというもので、それ故に$3$つの隣接整数の積は必ず$3$の倍数となります。$a^3-a=(a-1)a(a+1)$なので$3$の倍数です。
合同式を使うのは（２）からでしょう。
$a^3-b^3=(a-b)(a^2+ab+b^2)$なので$$a^2+ab+b^2 {\equiv}_{(3)} 0$$を示せば良いことになります。仮定より$a {\equiv}_{(3)} b$なので、$$\begin{align} a^2+ab+b^2 &{\equiv}_{(3)} a^2+a^2+a^2 \\ &{\equiv}_{(3)} 3a^2 \\ &{\equiv}_{(3)} 0 \end{align}$$となり、$a^3-b^3 {\equiv}_{(9)} 0$が示されます。
（３）は場合に分けます。
$a^3-b^3=(a-b)(a^2+ab+b^2) {\equiv}_{(3)} 0$のとき、
① $a-b {\equiv}_{(3)} 0$
または
② $a^2+ab+b^2 {\equiv}_{(3)} 0$
のいずれかが成立しますが、①のときは（２）で証明済みですので、②のときを示します。$a,b$を$3$を法とした余りで分類すると、$a^2+ab+b^2 {\equiv}_{(3)} 0$となるのは$a {\equiv}_{(3)} b$のときに限られることが分かります。$a,b$の剰余で分類した$a^2+ab+b^2$の剰余を以下のように表にしても良いでしょう。
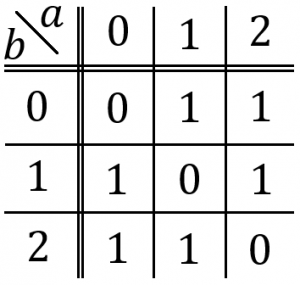結局 $a^2+ab+b^2 {\equiv}_{(3)} 0$ ならば $a {\equiv}_{(3)} b$ が言えるので
$a^3-b^3 {\equiv}_{(3)} 0$ならば$a^3-b^3 {\equiv}_{(9)} 0$
が示されます。
（コメント）
整数に熟達していれば少々物足りない問題かもしれませんね。
（2017/04/17追記：神戸大文系第3問に類題があります）
(2)も，合同式というほどのものではなく，
a^3-b^3=(a-b)^3+3ab(a-b)からただちに従いますね．
(3) 出題意図は，(1)を使うところにあるように思います．
a^3-b^3が3の倍数のとき，
(1)よりa-b=(a^3-b^3)-(a^3-a)+(b^3-b)も3の倍数．
よって，(2)よりa^3-b^3は9の倍数．
確かに（２）は$a^3-b^3=(a-b)^3+3ab(a-b)$という基本的な式変形により一発で示されますね。
また、（３）で（１）を利用すればよいことに気付けば、仰る通り（２）の結果も踏まえて鮮やかに証明することができます。
管理人は合同式が好きなので、つい何も考えずに合同式で処理してしまいがちなのですが(笑)、今回の様に誘導設問の意図を読み取ることができれば式変形だけで証明が片付いてしまいますね。
本問の本質を突いた別解を与えて下さったたけちゃん様に感謝致します。