半径1の球に内接する正四面体（北海道大学2005年前期数学文理共通）

解答例①

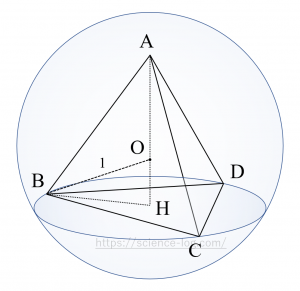
半径$1$の球に内接する正四面体$\mathrm{ABCD}$の一辺の長さを$a$、点$\mathrm{A}$から平面$\mathrm{BCD}$に下ろした垂線の足を$\mathrm{H}$、球の中心を$\mathrm{O}$とする。

点$\mathrm{H}$は$\mathrm{△}\mathrm{BCD}$の外心であるから正弦定理より$$2\mathrm{BH}={\displaystyle \frac{a}{\sin {60}^{\circ }}}$$ $$\therefore \mathrm{BH}={\displaystyle \frac{a}{\sqrt{3}}}$$となる。

$\mathrm{△}\mathrm{ABH}$について三平方の定理から$$\begin{array}{rl}\mathrm{AH}& =\sqrt{{\mathrm{AB}}^2-{\mathrm{BH}}^2}\\ & =\sqrt{a^2-{\left(\frac{a}{\sqrt{3}}\right)}^2}\\ & =\frac{\sqrt{6}}{3}a\end{array}$$と表せる。

同様に、$\mathrm{△}\mathrm{OBH}$について三平方の定理から$${\mathrm{BH}}^2+{\mathrm{OH}}^2=1^2$$ $$\therefore {\left({\displaystyle \frac{a}{\sqrt{3}}}\right)}^2+{({\displaystyle \frac{\sqrt{6}}{3}}a-1)}^2=1$$ $$\therefore a^2-\frac{2\sqrt{6}}{3}a=0$$ $$\therefore a=\frac{2\sqrt{6}}{3}(\because a>0)$$を得る。

故に、半径$1$の球に内接する正四面体の一辺の長さは$$\frac{2\sqrt{6}}{3}$$である。

解答例②

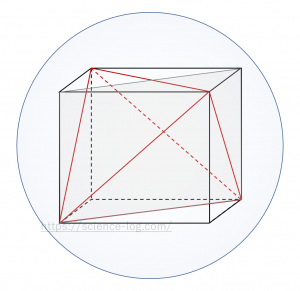
半径$1$の球に内接する正四面体は、半径$1$の球に内接する立方体から図のように切り出すことができる。

図の網掛け部分の断面に注目すると、この立方体の体対角線の長さは大円の直径に等しく、$2$であることが言える。立方体の体対角線と側面の対角線の長さの比は $\sqrt{3}:\sqrt{2}$ だから、半径$1$の球に内接する正四面体の一辺の長さは$$2\times {\displaystyle \frac{\sqrt{2}}{\sqrt{3}}}=\frac{2\sqrt{6}}{3}$$と求められる。