図形の重心を解析的に求める方法

本稿では積分を使って一般の図形の重心を求める方法を解説します。

 

 そもそも重心とは？

「重心」とは「質量をもつ図形に対して働く万有引力（重力）の合力の作用点」として定義される点のことを指します。

身近な例で考えてみましょう。手元に鉛筆がある人は、下の図のように人差し指で釣り合いのとれる位置を探してみて下さい。このようにして、ちょうどバランスのとれるポイントが見つかるはずです。この位置が鉛筆の重心に相当します。

鉛筆全体に働く重力の合力は重心に集約されていると見なすことができて、実際に「万有引力（重力）の合力の作用点」になっています。そのため、重心をピンポイントで支えれば、鉛筆全体に働く重力と釣り合いが取れるのです。

物体（質量を有する物質の集合体）には例外なく重心が存在します。重心の位置を算出しておくと物理的な現象を考察する上で役立ちます。例えば、剛直な物体に働く重力は重心に集中して働くものとして考えることができるので、物体の運動を考えるのが簡単になります。

 

 重心を求める「公式」

重心がどこにあるのかを見つける一般的な方法を知っておくと便利です。高校物理の教科書には次のような公式が載っています。$$x_{\mathrm{G}}=\dfrac{m_{1} x_{1}+m_{2} x_{2}+\cdots}{m_{1}+m_{2}+\cdots}$$ここで$x_{\mathrm{G}}$というのは重心の座標を指しており、各質点の質量を$m_{1}$、$m_{2}$、…とし、質点の位置を$x_{1}$、$x_{2}$、…としています。

これは座標軸を自分で設定して計算により求める公式ですが、分割の難しい図形に適用するのは困難です。例えば下図のＡのような長方形を組み合わせた図形の重心は上の式を使って求められますが、Ｂのような曲線を含む図形の重心は求めることができません。

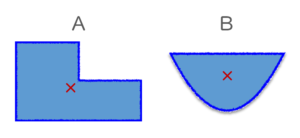
そこでＢのような場合では「面積の細分を考える」という積分の考え方に似た方法で重心を求めます。分かりやすくするために直角二等辺三角形を例に考えてみましょう。

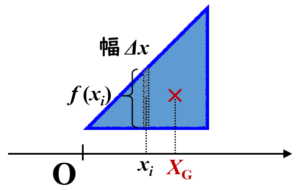
直角二等辺三角形の面積全体（$S$と置く）を極めて細い長方形に分割して、すべての長方形を足し合わせて重心（加重平均）を考えます。ここでは図形の質量は一様であると仮定しています。

この直角二等辺三角形の質量を$M$とし、斜線部の長方形の面積を$\varDelta S_i$とすると、斜線部の質量$\varDelta m_i$は全体に対する質量の割合を考えて$$\varDelta m_i=\dfrac{\varDelta S_i}{S} \times M$$と表すことができます。

いま、斜線部の重心の位置を$x_i$とすれば、重心の位置$x_{\mathrm{G}}$は和の記号を用いて$$\begin{align} x_{\mathrm{G}}&=\dfrac{\displaystyle \sum_{i=1}^{n}\varDelta m_i x_i }{\displaystyle \sum_{i=1}^{n}\varDelta m_i} \\ &= \dfrac{\displaystyle \sum_{i=1}^{n}\dfrac{\varDelta S_i}{S} M x_i }{\displaystyle \sum_{i=1}^{n}\dfrac{\varDelta S_i}{S} M} \\ &= \dfrac{\displaystyle \sum_{i=1}^{n}\varDelta S_i x_i }{\displaystyle \sum_{i=1}^{n}\varDelta S_i} \end{align}$$と表現できます（途中で約分しています）。さらに斜線部の長方形の幅を$\varDelta x$、縦の長さを$f(x_i)$とすれば、$\varDelta S_i=f(x_i)\varDelta x$ なので$$\begin{align} x_{\mathrm{G}}&=\dfrac{\displaystyle \sum_{i=1}^{n} f(x_i) x_i \varDelta x }{\displaystyle \sum_{i=1}^{n} f(x_i)\varDelta x} \end{align}$$となります。これは $n \to \infty$ として$\varDelta x$を極限まで小さくとれば、区分求積法の考え方に従って積分表示に書き直すことができ、重心の位置は$$\color{red}{x_{\mathrm{G}}=\dfrac{\displaystyle \int_{0}^{L} f(x)x \, d x }{\displaystyle \int_{0}^{L} f(x) \, d x}}$$で与えられます。ここで$L$は適当な積分区間の上限です。

これが今回紹介する重心の公式です。このように面積の細分を考えることによって、関数の積分を用いて重心の位置を求めることができます。

 

 直角二等辺三角形の重心

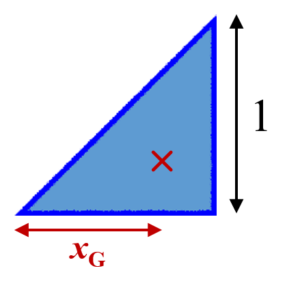
上記の公式により、等辺の長さが$1$の直角二等辺三角形の重心の位置$x_{\mathrm{G}}$は、$$\begin{align} x_{\mathrm{G}}&=\dfrac{\displaystyle \int_{0}^{1} x \times x \, d x }{\displaystyle \int_{0}^{1} x \, d x} \\ &= \dfrac{\left[\dfrac{1}{3}x^3\right]_{0}^{1}}{\left[\dfrac{1}{2}x^2\right]_{0}^{1}} \\ &= \dfrac{1}{3} \times \dfrac{2}{1} \\ &= \dfrac{2}{3} \end{align}$$と求められます。また、高さ方向の重心の位置$y_{\mathrm{G}}$は同様に考えて$$y_{\mathrm{G}}=\dfrac{\displaystyle \int_{0}^{1} (1-x) \times x \, d x }{\displaystyle \int_{0}^{1} x \, d x}=\dfrac{1}{3}$$と求められます。これが正しいことは重心ベクトルの公式などから確認できます。

 

 放物線の重心

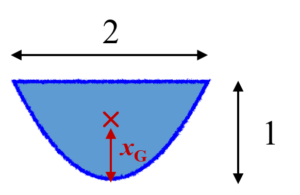
公式を使えば上図のような放物線が囲む図形の面積も求められます。$$\begin{align} x_{\mathrm{G}}&=\dfrac{\displaystyle \int_{0}^{1} 2\sqrt{x} \times x \, d x }{\displaystyle \int_{0}^{1} 2\sqrt{x} \, d x} \\ &= \dfrac{2\left[\dfrac{2}{5}x^{\frac{5}{2}}\right]_{0}^{1}}{2\left[\dfrac{2}{3}x^{\frac{3}{2}}\right]_{0}^{1}} \\ &= \dfrac{3}{5} \end{align}$$頂点からの距離が$x$のとき、微小長方形の横幅は$2\sqrt{x}$であることに注意してください。

 

 半円の重心

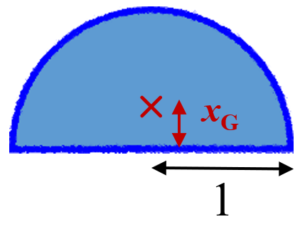
半径が$1$である半円の重心を求めてみます。弦からの距離が$x$のとき、微小長方形の横幅が$2\sqrt{1-x^2}$であることに注意すると、$$x_{\mathrm{G}}=\dfrac{\displaystyle \int_{0}^{1} 2\sqrt{1-x^2} \times x \, d x }{\displaystyle \int_{0}^{1} 2\sqrt{1-x^2} \, d x}$$となります。ここで$\displaystyle \int_{0}^{1} 2\sqrt{1-x^2} \, d x$は半径$1$の半円の面積なので$\dfrac{\pi}{2}$であり、$-\dfrac{2}{3}(1-x^2)^{\frac{3}{2}}$ を微分すると $2x\sqrt{1-x^2}$ となるので、$$\begin{align} x_{\mathrm{G}}&=\dfrac{\left[-\dfrac{2}{3}(1-x^2)^{\frac{3}{2}}\right]_{0}^{1}}{\dfrac{\pi}{2}} \\ &= \dfrac{2}{3}\times \dfrac{2}{\pi} \\ &= \dfrac{4}{3 \pi} \end{align}$$と求められます。

 

 半球の重心

以上の方法は平面図形だけでなく立体図形にも応用可能です。最後に半径が$1$である半球の重心を求めてみましょう。

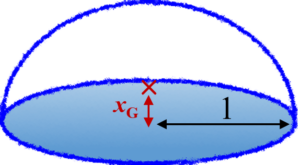
底面からの高さが$x$のとき、微小円柱の底面積が$(1-x^2)\pi$であることに注意すると、$$\begin{align} x_{\mathrm{G}}&=\dfrac{\displaystyle \int_{0}^{1} (1-x^2)\pi \times x \, d x }{\displaystyle \int_{0}^{1} (1-x^2)\pi \, d x} \\ &=\dfrac{\displaystyle \int_{0}^{1} (x-x^3) \, d x }{\displaystyle \int_{0}^{1} (1-x^2) \, d x} \\ &=\dfrac{\left[\dfrac{1}{2}x^2-\dfrac{1}{4}x^4\right]_{0}^{1}}{\left[x-\dfrac{1}{3}x^3\right]_{0}^{1}} \\ &= \dfrac{1}{4}\times \dfrac{3}{2} \\ &= \dfrac{3}{8} \end{align}$$と求められます。

 

---

---