積分方程式の基礎的な問題ですが、被積分関数に絶対値が付いています。このパターンでは場合分けが発生するので注意が必要です。
《問題》
関数$f(x)$が$$f(x)=x^{2}-x \int_{0}^{2}|f(t)|\,dt$$を満たしているとする。このとき、$f(x)$を求めよ。
(東北大学2007年 前期文系第4問)
《考え方》
定積分 $\displaystyle \int_{0}^{2}|f(t)|\,dt$ は結局のところ定数になるので、これを$a$などと文字で置くことができます。すると関数$f(x)$は$$f(x)=x^{2}-ax$$と表せるので$$a=\displaystyle \int_{0}^{2}|t^{2}-at|\,dt$$という方程式が成立します。後はこれを中身の正負に注意しつつ解くだけです。
● ● ●
解答例
定数$a$を用いて $a=\displaystyle \int_{0}^{2}|f(t)|\,dt$ と置くと、関数$f(x)$は$$f(x)=x^{2}-ax$$と表せて、方程式$$a=\displaystyle \int_{0}^{2}|t^{2}-at|\,dt \quad \cdots (*)$$が成立する。
(i) $0 \leqq a <2$ のとき、右辺は$$\small \begin{aligned}
\text{(右辺)} &=\int_{0}^{a}\left(a t-t^{2}\right) d t+\int_{a}^{2}\left(t^{2}-a t\right) d t \\
&=\left[\frac{a t^{2}}{2}-\frac{t^{3}}{3}\right]_{0}^{a}+\left[\frac{t^{3}}{3}-\frac{a t^{2}}{2}\right]_{a}^{2} \\
&=\frac{a^{3}}{6}+\left\{\left(\frac{8}{3}-2 a\right)-\left(-\frac{a^{3}}{6}\right)\right\} \\
&=\frac{a^{3}}{3}-2 a+\frac{8}{3}
\end{aligned}$$となるから、方程式$(*)$を解くと、$$a^{3}-9 a+8=0$$ $$\therefore (a-1)\left(a^{2}+a-8\right)=0$$ $$\therefore a=1,\ \frac{-1 \pm \sqrt{33}}{2}$$を得る。このうち $0 \leqq a <2$ を満たすものは $a=1$ に限る。
(ii) $a \geqq 2$ のとき、右辺は$$\small \begin{aligned}
\text{(右辺)} &=\int_{0}^{2}\left(a t-t^{2}\right) d t \\
&=\left[\frac{a t^{2}}{2}-\frac{t^{3}}{3}\right]_{0}^{2} \\
&=2 a-\frac{8}{3}
\end{aligned}$$となるから、方程式$(*)$を解くと、$$a=\frac{8}{3}$$を得る。これは $a \geqq 2$ を満たしている。
以上、(i)、(ii)より、求める関数$f(x)$は$$\color{red}{x^{2}-x, \quad x^{2}-\frac{8}{3} x}$$の2つである。
(コメント)
被積分関数に絶対値が付いているので、積分値は面積と捉えることができます。
(i) $0 \leqq a <2$ のとき、定積分は以下の面積に相当します。
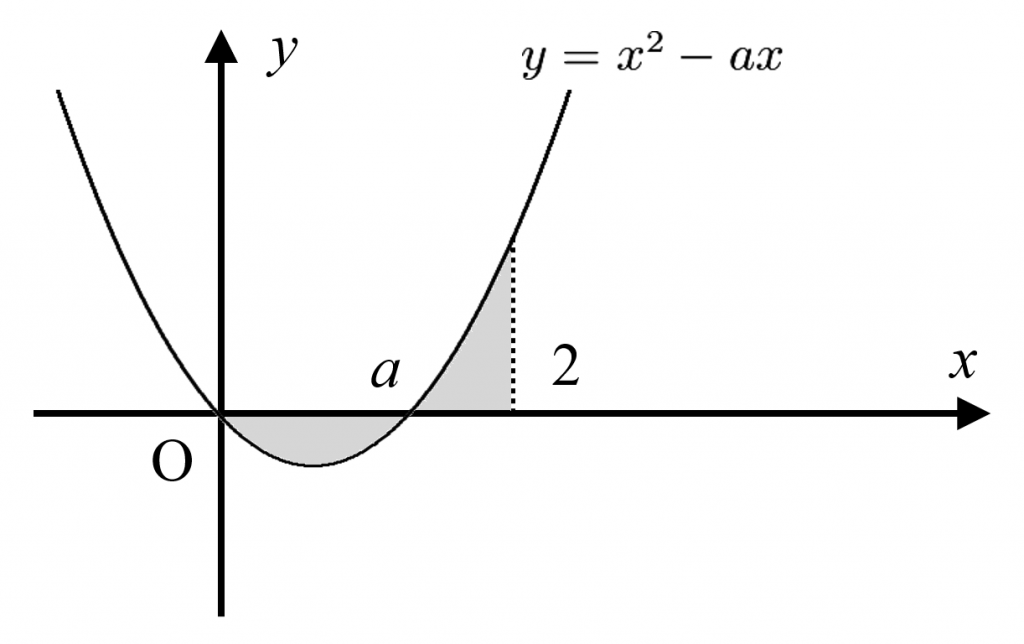
また、(ii) $a \geqq 2$ のとき、定積分は以下の面積に相当します。
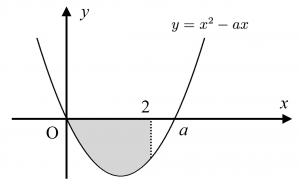
このように面積を考えると場合分けの必要性がビジュアル化できるので、理解の助けになります。
