今回は東大理系数学の過去問から回転体の求積問題を取り上げます。
座標空間内を、長さ$2$の線分$\mathrm{AB}$が次の2条件(a)、(b)をみたしながら動く。
(a) 点$\mathrm{A}$は平面 $z=0$ 上にある。
(b) 点$\mathrm{C}(0,0,1)$が線分$\mathrm{AB}$上にある。
このとき、線分$\mathrm{AB}$が通過することのできる範囲を$K$とする。$K$と不等式 $z \geqq 1$ の表す範囲との共通部分の体積を求めよ。
(2016年東京大学前期理系 第6問)
考え方
線分$\mathrm{AB}$が$z$軸のまわりで対称であることから、立体$K$が$z$軸まわりの回転体になります。このことは問題文を一見してまず気付きたい点です。この事実を踏まえれば、線分$\mathrm{CB}$の通過領域を$xz$平面上で議論すればよいことが分かります。ここでその後の計算量に差が付きます。
立体$K$は$z$軸に関して回転対称なので、$xz$平面による$K$の断面について $z=t$ と固定したときの点$\mathrm{B}$の$x$座標を求められれば、後は完答まで一直線です。積分計算ではケアレスミスに注意しましょう。
解答例
長さ$2$の線分$\mathrm{AB}$は点$\mathrm{C}(0,0,1)$を通り、点$\mathrm{A}$は平面 $z=0$ 上を自由に動き回る。また、線分$\mathrm{AB}$が平面 $z=t$($1 \leqq t \leqq 2$)と交点を持つとき、点$\mathrm{B}$の$z$座標が増加するにつれて交点の$x$座標は単調減少する。これより、$xz$平面上において線分$\mathrm{AB}$が通過することのできる範囲のうち $z \geqq 1$ を満たす部分を$D$とすれば、立体$K$は$D$を$z$軸周りに一回転させてできる立体に一致する。
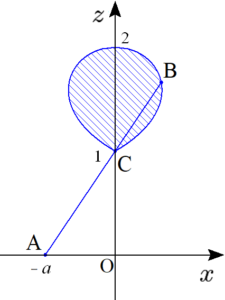
$a>0$ とし、点$\mathrm{A}$の座標を$(-a,0,0)$と置く。このとき$\overrightarrow{\mathrm{AC}}=\left(a,\,0,\,1\right)$であるから、$$\begin{align} \overrightarrow{\mathrm{OB}}&=\overrightarrow{\mathrm{OA}}+ \overrightarrow{\mathrm{AB}} \\ &=\overrightarrow{\mathrm{OA}}+2 \dfrac{ \overrightarrow{\mathrm{AC}}}{\left|\overrightarrow{\mathrm{AC}}\right|} \\ &=\left(-a+\dfrac{2a}{\sqrt{a^2+1}},\,0,\,\dfrac{2}{\sqrt{a^2+1}}\right) \end{align}$$となる。ここで点$\mathrm{B}$の$z$座標を$t$(ただし $1 \leqq t \leqq 2$)と置くと、$t=\dfrac{2}{\sqrt{a^2+1}}$ であり、$$a=\dfrac{\sqrt{4-t^2}}{t}$$と表せる。よって、点$\mathrm{B}$の$x$座標を$X$とし、$X$を$t$で表すと、$$\begin{align} X &= -a+\dfrac{2a}{\sqrt{a^2+1}} \\ &=a \left(-1+\dfrac{2}{\sqrt{a^2+1}}\right) \\ &=\dfrac{\sqrt{4-t^2}}{t}\left(-1+t\right) \end{align}$$となる。
これより、$z=t$ における立体$K$の断面積$S(t)$は$$\begin{align} S(t) &= \pi X^2 \\ &= \dfrac{\pi(4-t^2)(t-1)^2}{t^2} \end{align}$$となる。よって、立体$K$の $z \geqq 1$ の部分の体積$V$は$$\small \begin{align} V &= \displaystyle \int_{1}^{2} S(t) \, dt \\ &= \displaystyle \pi \int_{1}^{2} \dfrac{(4-t^2)(t-1)^2}{t^2} \, dt \\ &= \displaystyle \pi \int_{1}^{2} \left(-t^2+2t+3-\dfrac{8}{t}+\dfrac{4}{t^2}\right) \, dt \\ &= \pi \left[-\dfrac{1}{3}t^3+t^2+3t-8 \log t-\dfrac{4}{t}\right]_{1}^{2} \\ &= \pi\left(-\dfrac{7}{3}+3+3-8 \log 2+2\right) \\ &= \color{red}{\pi\left(\dfrac{17}{3}-8 \log 2\right)} \end{align}$$と求められる。

積分すべき断面積の式が正しいことを示すために、解答の中で点$\mathrm{B}$の軌跡の形状($z$座標の変化が単調であること、平面 $z=t$ との交点の$x$座標の変化が単調であること、など)に触れておく必要があります。ここが抜けていると$t$の値によって断面積の式に場合分けが必要となる可能性を棄却できていない答案になってしまいます。
参考のために立体$K$の $z \geqq 1$ の部分の立体図を示しておきます。
$z$軸を含むある平面上における点$\mathrm{B}$の軌跡を求めてしまえば勝ち、ということに気が付けると比較的見通し良く解答できます。予備校の解答速報では難~やや難に分類されていたようですが、体積計算の際に場合分けが不要であり、基礎的な計算力さえあれば十分完答可能なレベルだと思います。
問題の立体図形がある直線に関して回転対称的 ⇒ ある直線を通る平面で立体の断面を考える ⇒ 積分、という流れに乗れれば空間認識の苦手な人でも機械的に体積計算まで辿り着けるはずです。回転軸の有無に関わらず、取り敢えず適当な平面で切って断面図を考えるというのは立体図形問題を解く上での定石ですね。
別解としては、上記の回答例と同様に点$\mathrm{B}$の範囲を $x>0$ の範囲に限り、$\angle \mathrm{OCA}= \theta$ などと置いて三角関数により点$\mathrm{B}$の座標を表す方法などがあります。この方針によれば$$\mathrm{B}(2 \sin \theta-\tan \theta, \, 0, \, 2 \cos \theta)$$と表せますが、三角関数のまま積分計算に突入するとやや煩雑な計算をこなす必要があります。
因みに、本問の点$\mathrm{B}$の軌跡は「ニコメデスのコンコイド」と呼ばれる曲線に相当します。ニコメデスはコンコイド曲線を研究した古代ギリシャの数学者の名前です。
(2021/10/02追記)
2014年の東工大実戦模試の第3問に「ニコメデスのコンコイド」を題材とする求積問題が出題されています。こちらは体積ではなく曲線の囲む領域の面積を求める問題です。