対称軸をもつ立体の求積③（1991年一橋大学後期数学第4問）

解答例

点$\mathrm{P}$の存在する範囲は線分$\mathrm{AB}$を回転軸とする回転体である。そこで、点$\mathrm{A}$を原点、点$\mathrm{B}$を$(4,0,0)$として平面 $z=0$ 上の $y\geqq 0$ で点$\mathrm{P}$の存在する範囲を考える。点$\mathrm{P}$を$(x,y,0)$と置くと、条件(ⅰ)～(ⅲ)はそれぞれ$$\{\begin{array}{l}\sqrt{x^2+y^2}\leqq 4\\ 4\leqq 4x\leqq 8\\ 4x\leqq 2\sqrt{2}\sqrt{x^2+y^2}\end{array}$$すなわち$$\{\begin{array}{ll}\sqrt{x^2+y^2}\leqq 4& \cdots \mathrm{①}\\ 1\leqq x\leqq 2& \cdots \mathrm{②}\\ \sqrt{2}x\leqq \sqrt{x^2+y^2}& \cdots \mathrm{③}\end{array}$$となる。$\mathrm{②}$より $x>0$ だから$$\mathrm{③}⟺2x^2\leqq x^2+y^2$$ $$\therefore x^2\leqq y^2\cdots {\mathrm{③}}^{\prime }$$であり、$y\geqq 0$ より、${\mathrm{③}}^{\prime }$は$$x\leqq y\cdots \mathrm{④}$$に一致する。$\mathrm{①}$、$\mathrm{②}$、$\mathrm{④}$より、平面 $z=0$ 上の $y\geqq 0$ の部分で点$\mathrm{P}$の存在する領域は以下の図の赤色斜線部となる。これを$x$軸のまわりに1回転してできる立体が点$\mathrm{P}$の存在する範囲である。

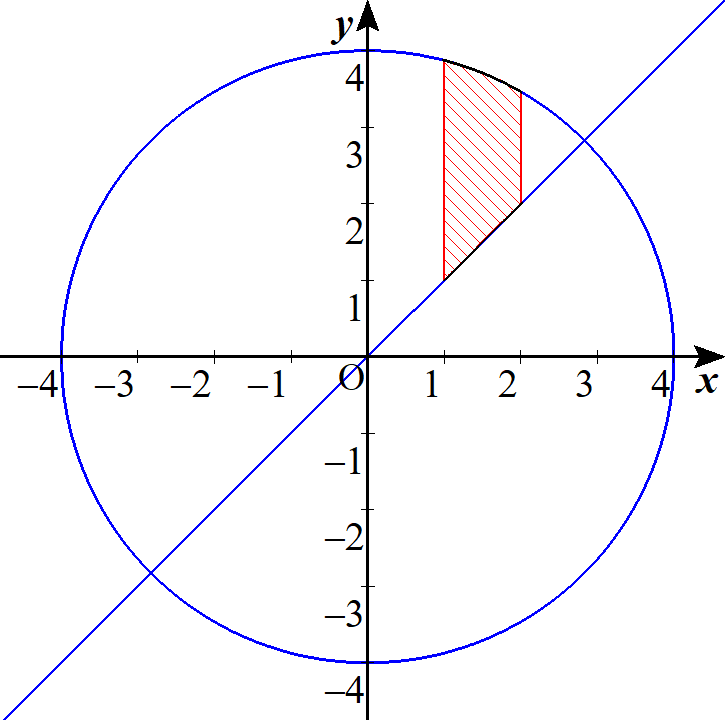
よって、求める立体の体積を$V$とすると、$$\begin{array}{rl}V& ={\displaystyle {\int }_1^2\pi \{(16-x^2)-x^2\}dx}\\ & ={\displaystyle 2\pi {\int }_1^2(8-x^2)dx}\\ & =2\pi {[8x-{\displaystyle \frac{1}{3}}{x}^3]}_1^2\\ & =2\pi (8-{\displaystyle \frac{7}{3}})\\ & ={\displaystyle \frac{34}{3}}\pi \end{array}$$となる。