一見して回転体と分かりにくい立体シリーズの筆頭です。計算自体は難しくありませんが、断面を調べるところでつまづく受験生が出てきそうな問題です。
$a$は与えられた実数で、$0<a \leqq 1$ を満たすものとする。$xyz$空間内に1辺の長さ$2a$の正三角形$\triangle \mathrm{PQR}$を考える。辺$\mathrm{PQ}$は$xy$平面上にあり、$\triangle \mathrm{PQR}$を含む平面は$xy$平面と垂直で、さらに点$\mathrm{R}$の$z$座標は正であるとする。
(1)辺$\mathrm{PQ}$が$xy$平面の単位円の内部(周を含む)を自由に動くとき、$\triangle \mathrm{PQR}$(内部を含む)が動いてできる立体の体積$V$を求めよ。
(2)$a$が $0<a \leqq 1$ の範囲を動くとき、体積$V$の最大値を求めよ。
(1996年京都大学後期理系 第5問)
考え方
大雑把に$\triangle \mathrm{PQR}$の立体的なイメージを考えてみましょう。「$\triangle \mathrm{PQR}$を含む平面は$xy$平面と垂直」とあるので、題意の立体を$z$軸に垂直な平面で切れば良さそうだと分かります。
この平面内で$\triangle \mathrm{PQR}$の通過する領域を考えるのですが、これがどんな図形になるのかを把握する必要があります。ここで詰まってしまうと先に進めません。「辺$\mathrm{PQ}$が$xy$平面の単位円の内部(周を含む)を自由に動く」とあるので、まず極端な場合、つまり点$\mathrm{P}$、$\mathrm{Q}$が単位円の円周上に存在する場合を検討します。よくわからないという人は、まず$xy$平面上で辺$\mathrm{PQ}$が動く領域を調べてみましょう。
解答例
(1)
点$\mathrm{P}$、$\mathrm{Q}$が$xy$平面の単位円の円周上に存在する場合を考える。$\triangle \mathrm{PQR}$の辺$\mathrm{PR}$、$\mathrm{QR}$と平面 $z=t$($0 \leqq t \leqq \sqrt{3} a$)との交点を$\mathrm{S}$、$\mathrm{T}$と置き、線分$\mathrm{ST}$の中点を$\mathrm{U}$、点$(0,\,0,\,t)$を$\mathrm{H}$と置く。
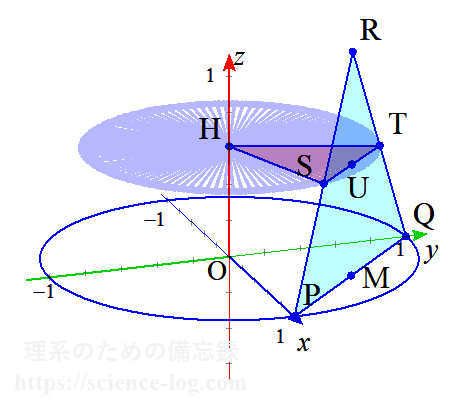
このとき、辺$\mathrm{PQ}$を平行移動すれば$\triangle \mathrm{PQR}$は$\triangle \mathrm{STH}$の範囲を通過し得る。よって、$\triangle \mathrm{PQR}$(内部を含む)が動いてできる立体を$K$とするとき、$K$の $z=t$ における断面は線分$\mathrm{SH}$を半径とする円となる。
これより、$K$の $z=t$ における断面積$A(t)$は線分$\mathrm{PQ}$の中点を$\mathrm{M}$とすれば$$\begin{align} A(t) &=\pi \mathrm{SH}^{2} \\ &=\pi\left(\mathrm{SU}^{2}+\mathrm{HU}^{2}\right) \end{align}$$となる。ここで$$\mathrm{HU}=\mathrm{OM}=\sqrt{1-a^{2}}$$であり、$$\mathrm{SU}:\mathrm{PM}=\mathrm{RU}:\mathrm{RM}$$より$$\mathrm{SU}: a=\sqrt{3} a-t: \sqrt{3} a$$となるから$$\mathrm{SU}=\dfrac{\sqrt{3} a-t}{\sqrt{3}}$$である。よって$$A(t)=\pi\left\{\dfrac{1}{3}(t-\sqrt{3} a)^{2}+1-a^{2}\right\}$$となるから、立体$K$の体積$V$は$$\begin{aligned}
V &=\int_{0}^{\sqrt{3} a} A(t) \, dt \\
&=\pi\left[\dfrac{1}{9}(t-\sqrt{3} a)^{3}+\left(1-a^{2}\right) t\right]_{0}^{\sqrt{3} a} \\
&=\color{red}{\dfrac{\sqrt{3}}{3} \pi\left(3 a-2 a^{3}\right)}
\end{aligned}$$と求められる。
(2)
(1)の結果より$$\dfrac{d V}{d a}=2 \sqrt{3} \pi\left(\dfrac{1}{2}-a^{2}\right)$$となるから、$V$を$a$の関数と見たときの増減は以下の表のようになる。$$\begin{array}{|c|c|c|c|c|c|}
\hline a & 0 & \cdots & \dfrac{\sqrt{2}}{2} & \cdots & 1 \\
\hline V^{\prime} & & + & 0 & – & \\
\hline V & & \nearrow & \dfrac{\sqrt{6}}{3} \pi & \searrow & \\
\hline
\end{array}$$よって、$a$が $0<a \leqq 1$ の範囲を動くとき、体積$V$の最大値は$$\color{red}{\dfrac{\sqrt{6}}{3} \pi}$$となる。

平面 $z=t$ による断面で$\triangle \mathrm{PQR}$の通過する領域を考えるのですが、「考え方」のところでも触れた通り、イメージしにくいという人はまず平面 $z=0$($xy$平面)上で辺$\mathrm{PQ}$の可動領域を調べてみるのが良いでしょう。辺$\mathrm{PQ}$が単位円の中しか動けないという制約により、これは$\mathrm{OP}$を半径とする円になります。あとはこれを平面 $z=t$ 上で考えるだけです。$\mathrm{PQ}$の長さを固定したときに、平面 $z=t$ で$z$軸から最も遠い$\triangle \mathrm{PQR}$内部の点がどこなのかを調べ、平面 $z=t$ 上でも円になることを確認します。ここで詰まってしまうと先に進めません。
参考のために、$a=\dfrac{\sqrt{2}}{2}$ のときに$\triangle \mathrm{PQR}$が動いてできる立体を図示しておきます。$z$軸に対して$\mathrm{PR}$がねじれの位置にあるので円錐台にはなりません。
ただし、この立体的なイメージは解答する上で必要という訳ではありません。断面積さえ求めてしまえば体積$V$は機械的に計算できます。