今年の徳島大入試では記進法が出題されましたが、学習指導要領が改訂され、整数分野からの出題が増えると予想されます。普通(?)の整数問題もしっかり対策しておくべきでしょう。
《問題》
次の問いに答えよ。
(1)不等式 $(x-1)^2-3|x-1|+1<0$ を満たす整数$x$をすべて求めよ。
(2)すべての自然数$n$に対して、$2^{n-1}+3^{3n-2}+7^{n-1}$ が$5$の倍数であることを、数学的帰納法を用いて証明せよ。
(徳島大学2013 理系前期(総合科)第1問)
《考え方》
(1)は不等式の絡む整数問題ですが、$x-1$ でまとまっているため絶対値があるにしては比較的取り組みやすいタイプです。
《(1)解答例 》
与不等式の左辺を$f(x)$と置けば、関数 $y=f(x)$ は直線 $x=1$ に関して対称であるから $x \geqq 1$ の範囲で調べれば十分である。このとき与不等式は$$(x-1)^2-3(x-1)+1<0$$となるので、$$\therefore \dfrac{3-\sqrt{5}}{2}<x-1<\dfrac{3+\sqrt{5}}{2}$$ $$\therefore \dfrac{5-\sqrt{5}}{2}<x<\dfrac{5+\sqrt{5}}{2}$$と$x$の範囲が $x \geqq 1$ で求まる。$2<\sqrt{5}<3$ より、$1<\dfrac{5-\sqrt{5}}{2}<\dfrac{3}{2}$、$\dfrac{7}{2}<\dfrac{5+\sqrt{5}}{2}<4$ と評価できるので、$x$の取り得る整数値は $x=2$ または $3$ となる。したがって $x \leqq 1$ の範囲も含めると、$$\color{red}{x=-1,0,2,3}$$となる。
(コメント)
$y=(x-1)^2-3|x-1|+1$ のグラフは以下のようになります。
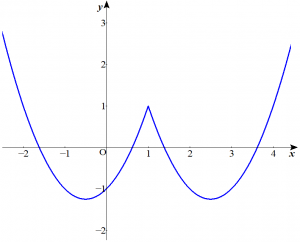 展開などはせずに $x-1$ をまとめたまま処理しましょう。計算の際は $t=x-1$ などと置いても良いと思います。
展開などはせずに $x-1$ をまとめたまま処理しましょう。計算の際は $t=x-1$ などと置いても良いと思います。
(2)ですが、問題文に帰納法で解けという指示があるので、それに従いましょう。
《(2)解答例 》
$a_n=2^{n-1}+3^{3n-2}+7^{n-1}$ と置き、$a_n$が任意の自然数$n$に対して$5$の倍数であることを示す。
$a_1=1+3+1=5$ より、$5$の倍数である。
ある自然数$k$に対して $a_k=2^{k-1}+3^{3k-2}+7^{k-1}$ が$5$の倍数であると仮定する。このとき、
$$\begin{align}
a_{k+1}
&=2^{k}+3^{3k+1}+7^{k} \\
&=2(a_{k}-3^{3k-2}-7^{k-1})+3^{3k+1}+7^{k} \\
&=2a_{k}+(-2+3^3) \cdot 3^{3k-2}+(-2+7) \cdot 7^{k-1} \\
&=2a_{k}+25 \cdot 3^{3k-2}+5 \cdot 7^{k-1}
\end{align}$$
となるので$a_{k+1}$も$5$の倍数である。したがって数学的帰納法により、任意の自然数$n$に対して $a_n=2^{n-1}+3^{3n-2}+7^{n-1}$は$5$の倍数であることが示された。
□
(コメント)
$2^{n-1}+3^{3n-2}+7^{n-1}$が任意の自然数$n$に対して$5$の倍数であることは、$\bmod{5}$ を使えば帰納法によらず、直接的に証明できます。別解として示しておきます。
《(2)別解 》
$a_n=2^{n-1}+3^{3n-2}+7^{n-1}$ と置き、$a_{n}$が任意の自然数$n$に対して$5$の倍数であることを示す。いま、計算しやすくするために$0$以上の整数$k$により $n=k+1$ と表し、$5$を法として$a_{k+1}$を調べる。
$$\begin{align}
a_{k+1}
&=2^{k}+3^{3k+1}+7^{k} \\
&=2^{k}+3 \cdot 27^{k}+7^{k} \\
&\equiv 2^{k}+3 \cdot 2^{k}+2^{k} \pmod{5} \\
&=5 \cdot 2^{k} \\
&\equiv 0 \pmod{5}
\end{align}$$
故に任意の$a_{n}$は$5$の倍数である。
□
(コメント)
現行の課程では合同式による解答が認められているので、合同式を使ったスマートな解答も作れるようにしたいですね。

(1)の解答例ですが,
「左辺が直線~に関して対称」は少し変な気もしました.
$x-1$をまとめて扱う代わりに $|x-1|$ をまとめて扱えば,
この表現を使わずに進めることができますね.
もちろん本質的には同じですが...
コメントありがとうございます。
ご指摘の箇所についてマイナーチェンジしてみました。
「左辺」を主語とするのは言われてみれば確かに奇妙な表現ですね・・・。
仰る通り、$\dfrac{3-\sqrt{5}}{2}<|x-1|<\dfrac{3+\sqrt{5}}{2}$のように解いても良いですね。
前問ともども,修正ありがとうございました.
本問については,意図をストレートに説明したものですから,
これが最も素直な(というか堂々としたというか)修正ですね.