今回も通過領域の良問を取り上げます。横浜国立大学の入試から。
$xy$平面上に点$(a,\,2)$を中心とし、原点$\mathrm{O}$を通る円$C$がある。$C$が放物線 $y=x^2$と異なる４点で交わるとき、次の問いに答えよ。
（１）$a$の満たす条件を求めよ。
（２）$a$が（１）で求めた条件を満たしながら変化するとき、$C$の動く範囲を図示せよ。
（2002年横浜国立大学(経済)前期 第4問）
考え方
「円$C$が放物線 $y=x^2$と異なる４点で交わる」という条件を（１）で求めます。まずは円$C$の方程式を$a$で表し、$y=x^2$と連立して$a$の満たすべき条件を求めます。（２）は逆像法、つまり「解の配置」の問題に置き換えて方程式が解をもつ条件を考えるのが良いでしょう。20分以内を目途に片付けたい問題です。
解答例
（１）
円$C$は点$(a,\,2)$を中心とし、原点$\mathrm{O}$を通るから、方程式は$$C:(x-a)^{2}+(y-2)^{2}=a^{2}+4$$ $$\therefore x^{2}-2 a x+y^{2}-4 y=0 \quad \cdots ①$$となる。
$①$と $y=x^2$ を連立すると、$$x^{2}-2 a x+x^{4}-4 x^{2}=0$$ $$x\left(x^{3}-3 x-2 a\right)=0 \quad \cdots ②$$を得る。円$C$が放物線 $y=x^2$と異なる４点で交わることは、$②$が異なる４つの実数解をもつことと同値である。これはつまり「（＊）方程式 $x^{3}-3 x-2 a=0$ が $x=0$ 以外の異なる３つの実数解をもつこと」と同値である。そこで、$f(x)=x^{3}-3 x-2 a$ と置いて増減を調べる。$$\begin{aligned} f^{\prime}(x) &=3 x^{2}-3 \\ &=3(x+1)(x-1) \end{aligned}$$より、増減表は以下のようになる。$$\begin{array}{|c|c|c|c|c|c|}
\hline x & \cdots & -1 & \cdots & 1 & \cdots \\
\hline f^{\prime}(x) & + & 0 & – & 0 & + \\
\hline f(x) & \nearrow & -2 a+2 & \searrow & -2 a-2 & \nearrow \\
\hline
\end{array}$$（＊）を満たすためには、$f(0)=-2a \ne 0$ かつ、関数$f(x)$の極大値と極小値の符号が異なればよい。よって、$a \ne 0$ および、$$f(-1) f(1)=(-2 a+2)(-2 a-2)<0$$を解いて $-1<a<1$ を得るから、求めるべき$a$の満たす条件は
$-1<a<1$ かつ $a \ne 0$
となる。
（２）
円$C$上の点$(X,\,Y)$が条件を満たす領域内に存在することと、$X^{2}-2 a X+Y^{2}-4 Y=0 \quad \cdots ③$ かつ $-1<a<1$、$a \ne 0$ を満たすような実数$a$が存在することは同値である。$③$を$$-2Xa+(X^{2}+Y^{2}-4 Y)=0$$と変形し、$a$の係数で場合分けして考える。
（ⅰ）$X=0$ のとき$$X^{2}+Y^{2}-4 Y=0$$より、$X=0, \ Y=\pm 4$ を得る。
（ⅱ）$X \ne 0$ のとき、$③$より$$a=\dfrac{X^{2}+Y^{2}-4 Y}{2 X}$$となるから、$$-1<\dfrac{X^{2}+Y^{2}-4 Y}{2 X}<1$$かつ$$X^{2}+Y^{2}-4 Y \ne 0$$が求めるべき条件である。これより$$\small \left(X^{2}+2 X+Y^{2}-4 Y\right)\left(X^{2}-2 X+Y^{2}-4 Y\right)<0$$ $$\small \therefore \left\{(X+1)^{2}+(Y-2)^{2}-5\right\}\left\{(X-1)^{2}+(Y-2)^{2}-5\right\}<0$$を得る。
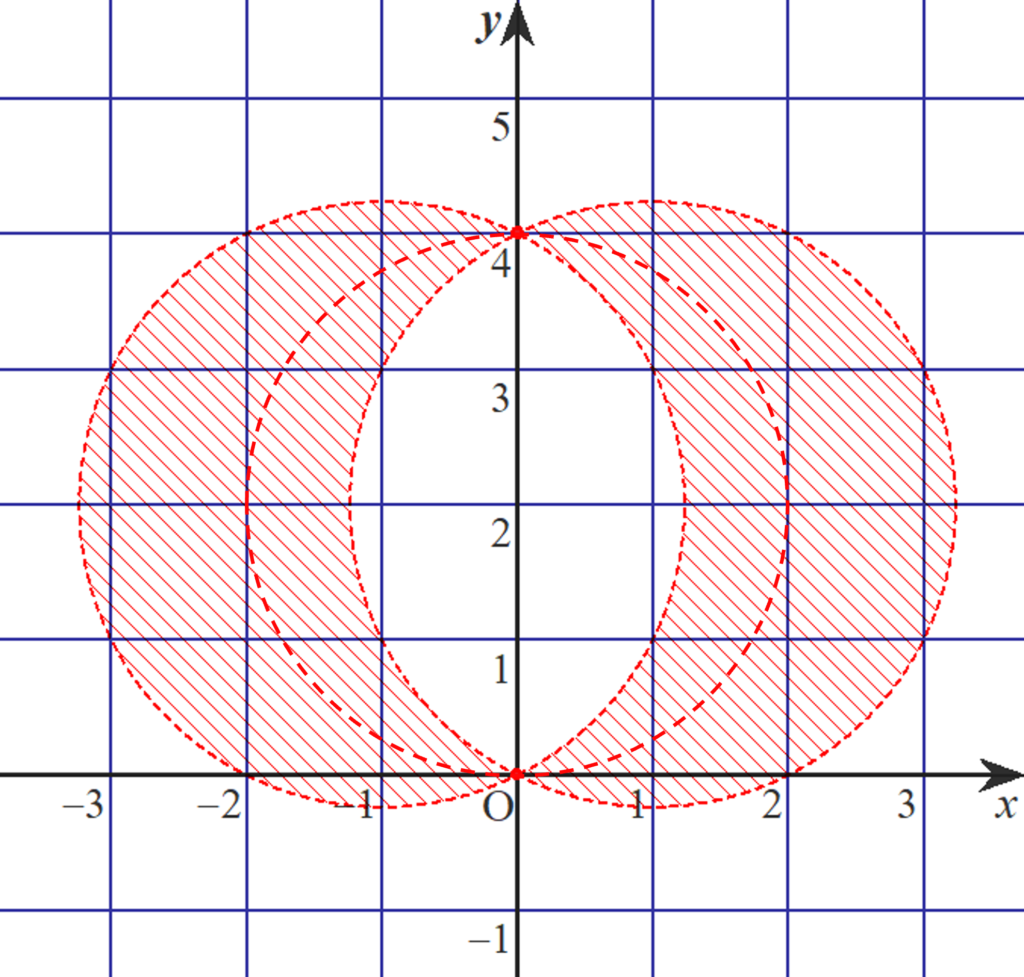
以上より、円$C$の動く範囲は下図の斜線部（赤色部分）である。ただし、境界線は含まず、２点$(0, \,\pm 4)$のみ含む。
（１）で$4$次式が登場していきなり手詰まりになったりしませんでしたか？「円$C$が放物線 $y=x^2$と異なる４点で交わる」という条件を座標平面上で考えれば、４つの交点の分だけ$x$座標が出てくるはずだ、と見当が付きます。これが解答例中の$4$次式$②$に対応しています。因数分解すれば$3$次式が出てくるので、異なる３つの実数解を持つ条件に読み替えれば増減を調べて$a$の満たすべき条件が求められそうだと見通しが付くはずです。
それから、$③$式は$a$に関する$1$次式ですが、解答の根拠は逆像法によるものです。逆像法は「パラメータを含む方程式が（実数の）解をもつような点$\small (x,y)$の条件を求める」という考え方のことであり、二次方程式が出てこなくても「逆像法」です。
本問のレベルが試験本番で卒無くこなせれば基礎の実力は問題ないと思います。こうした「解答を一見すると簡単そうな問題」こそ試験会場でミスしやすいものです。ありがちなミスですが、$a \ne 0$ の条件を忘れて$y$軸上の点が抜けていたりしないでしょうか？ ほんのちょっとしたケアレスミスが合否を左右します。
なお、「円$C$が放物線 $y=x^2$と異なる４点で交わる」という条件を満たすとき、円$C$の動く範囲はちゃんと今回求めた領域に一致しています。円の中心を動かして確かめてみて下さい。余裕のある人は「円$C$が放物線 $y=x^2$と異なる３点で交わる」場合を考えてみるのも面白いかもしれません。
通過領域問題の苦手意識は早めに解消しておきましょう。通過領域の問題の解き方や考え方については「通過領域問題の攻略法」のシリーズで詳しく解説しているので是非参考にして下さい！