放物線にまつわる面積公式②（例題編）

●　　　●　　　●

《マジメな解答例》

$y=x^2-6x+12$ より、$y’=2x-6$ となるから、接線$l$の方程式は$$y=(2t-6)(x-t)+(t^2-6t+12)$$ $$\therefore y=\fbox{2}(t-\fbox{3})x-\fbox{1}t^2+\fbox{12}$$となる。これが点$(2,0)$を通るから $(x,y)=(2,0)$ を代入して$$0=4(t-3)-t^2+12$$より、$$\therefore t=\fbox{0}、\fbox{4}$$を得る。以下、$t=4$ であるから接線$l$の方程式は $y=2x-4$ となる。

面積$S_1$は

$\begin{align}
S_1&=\int^{4}_{0} \{(x^2-6x+12)-(2x-4)\}dx \\
&=\int^{4}_{0} (x^2-8x+16)dx \\
&=\left[ \dfrac{1}{3} x^3-4x^2+16x \right]^{4}_{0} \\
&=\dfrac{\fbox{64}}{\fbox{3}}
\end{align}$

法線$m$の方程式は$$y=-\dfrac{1}{2}(x-4)+4$$ $$\therefore y=\dfrac{\fbox{-1}}{\fbox{2}}x+\fbox{6}$$となるから、放物線$\mathrm{C}$と法線$m$の交点の$x$座標は、$$x^2-6x+12=-\dfrac{1}{2}x+6$$ $$\therefore x=\dfrac{3}{2}、4$$と求められる。よって面積$S_2$は

$\begin{align}
S_2&=\int^{4}_{\frac{3}{2}} \left\{\left(-\dfrac{1}{2}x+6\right)-(x^2-6x+12)\right\}dx \\
&=\int^{4}_{\frac{3}{2}} \left(-x^2+\dfrac{11}{2}x-6\right)dx \\
&=\left[ -\dfrac{1}{3} x^3+\dfrac{11}{4}x^2-6x \right]^{4}_{\frac{3}{2}} \\
&=-\dfrac{4}{3}-\left(-\dfrac{63}{16}\right) \\
&=\dfrac{\fbox{125}}{\fbox{48}}
\end{align}$

図形の位置関係は以下の図のようになっている。

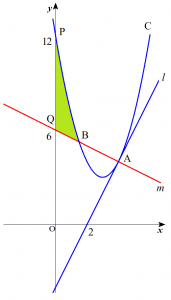よって面積$S_3$は

$\begin{align}
S_3&=\int^{\frac{3}{2}}_{0} \left\{(x^2-6x+12)-\left(-\dfrac{1}{2}x+6\right)\right\}dx \\
&=\int^{\frac{3}{2}}_{0} \left(x^2-\dfrac{11}{2}x+6\right)dx \\
&=\left[ \dfrac{1}{3} x^3-\dfrac{11}{4}x^2+6x \right]^{\frac{3}{2}}_{0} \\
&=\dfrac{63}{16}-0 \\
&=\dfrac{\fbox{63}}{\fbox{16}}
\end{align}$

と求められる。

» 閉じる

●　　　●　　　●

《公式を使った解答例》

$y=x^2-6x+12$ より、$y’=2x-6$ となるから、接線$l$の方程式は$$y=(2t-6)(x-t)+(t^2-6t+12)$$ $$\therefore y=\fbox{2}(t-\fbox{3})x-\fbox{1}t^2+\fbox{12}$$となる。これが点$(2,0)$を通るから $(x,y)=(2,0)$ を代入して$$0=4(t-3)-t^2+12$$より、$$\therefore t=\fbox{0}、\fbox{4}$$を得る。以下、$t=4$ であるから接線$l$の方程式は $y=2x-4$ となる。（ここまではマジメな解答例と同じ）

面積$S_1$は「$\dfrac{1}{3}$公式」より、$$S_1=\dfrac{1}{3}(4-0)^3=\dfrac{\fbox{64}}{\fbox{3}}$$と求められる。（☜時間短縮！）

法線$m$の方程式は$$y=-\dfrac{1}{2}(x-4)+4$$ $$\therefore y=\dfrac{\fbox{-1}}{\fbox{2}}x+\fbox{6}$$となるから、放物線$\mathrm{C}$と法線$m$の交点の$x$座標は、$$x^2-6x+12=-\dfrac{1}{2}x+6$$ $$\therefore x=\dfrac{3}{2}、4$$と求められる。（法線の求め方もマジメな解答例と同じ）

よって面積$S_2$は「$\dfrac{1}{6}$公式」より、

$\begin{align}
S_2
&=\dfrac{1}{6}\left(4-\dfrac{3}{2}\right)^3 \\
&=\dfrac{1}{6} \cdot \left(\dfrac{5}{2}\right)^3 \\
&=\dfrac{\fbox{125}}{\fbox{48}}
\end{align}$

と求められる。（☜時間短縮！）

$S_3$を求めるが、ここで$\triangle{\mathrm{BPQ}}$に着目する。$\triangle{\mathrm{BPQ}}$の面積は$$\dfrac{1}{2} \cdot 6 \cdot \dfrac{3}{2}=\dfrac{9}{2}$$である。また、放物線$\mathrm{C}$と線分$\mathrm{PB}$によって囲まれる図形の面積を$S_4$とすると、$S_4$は「$\dfrac{1}{6}$公式」より、

$\begin{align}
S_4
&=\dfrac{1}{6}\left(\dfrac{3}{2}-0\right)^3 \\
&=\dfrac{1}{6} \cdot \left(\dfrac{3}{2}\right)^3 \\
&=\dfrac{9}{16}
\end{align}$

と求められる。よって

$\begin{align}
S_3
&=\triangle{\mathrm{BPQ}}-S_4 \\
&=\dfrac{9}{2}-\dfrac{9}{16} \\
&=\dfrac{\fbox{63}}{\fbox{16}}
\end{align}$

となる。（☜時間短縮！）

※実際にはこんなに日本語を書く必要は無いのでもっと短い労力で解答可能です。センター試験の第２問は、余白にインテグラル等を書き込んでいる暇があったらさっさと公式で片付けた方が良いでしょう。ここで時間が稼げたら数ⅡBで９割は確実です。

» 閉じる