放物線に接する指数関数を求めてみよう

本稿では、誰もが一度は考えたことのあるであろう(？)「放物線に接する指数関数」を求めてみます。前回に引き続き「ランベルトのW関数」に登場してもらいます！

 

 放物線と指数関数

放物線と指数関数の位置関係を考えてみます。下の図に青色が $y=x^2$、赤色が $y=a^x$（$a>1$）のグラフを示します。緑色の点を左右に動かして$a$の値を変えることができます。

$a$の値を色々と変えていると、ある$a$の値でちょうど放物線と指数関数が接することが観察されます。この値は$2$にとても近い値ですが、どうやら$2$ではないようです。グラフを観察していると、大体$2.087…$くらいの微妙な数であることが分かります。

実はこの値は解析的に求めることができます。

 

 ランベルトのW関数（再登場）

放物線と指数関数が接するためには、まず共有点を持たなければなりません。そこで、共有点の$x$座標を$t$と置きます（$t$は明らかに正の実数）。

このとき、$t$は方程式$$t^2=a^t$$を満たします。このような実数$t$を求めるために、前回の「方程式$2^x=x^2$の解について」でも扱った「ランベルトのW関数」に再登場してもらいます。

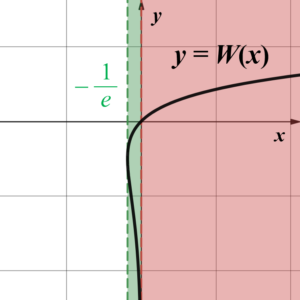
ランベルトのW関数とは「関数$y=xe^x$の逆関数」のことでした。

上図のように、関数 $y=W(x)$ は $y \geqq -1$ の部分（赤色部分；$W_{0}(x)$）と $y \leqq -1$ の部分（青色部分；$W_{-1}(x)$）に分けることができます。つまり、関数 $y=W(x)$ は $-\dfrac{1}{e} \leqq x <0$ の範囲では2価関数（一つの$x$の値に対して$y$の値を$2$つ与える関数）となります。

 

 $a$の値を求める

ランベルトのW関数についておさらいしたところで、早速、方程式を解いてみましょう。

方程式 $t^2 = a^t$ の両辺に自然対数をとり、$$2 \log |t| = t \log a$$ $$\therefore t^{-1} \log |t| = \frac{1}{2} \log a$$ $$\therefore t^{-1} \log |t| = \log \sqrt{a}$$と整理します。

いま、$t>0$ の場合を考えるので、絶対値を外すと$$t^{-1} \log t = \log \sqrt{a}$$となります。ここで $t^{-1}=e^{- \log t}$ により、$$\log t \, e^{- \log t} =\log \sqrt{a}$$ $$\therefore -\log t \, e^{- \log t} =-\log \sqrt{a}$$となります。この両辺についてランベルトのW関数をとると、$$W\left(-\log t \, e^{- \log t}\right) = W(-\log \sqrt{a})$$ $$\therefore -\log t = W(-\log \sqrt{a})$$ $$\therefore t = \color{red}{e^{-W(-\log \sqrt{a})}}$$を得ます。途中でW関数について $W(x e^x)=x$ の関係が成り立つことを利用しました。

---

さて、共有点の$x$座標は$e^{-W(-\log \sqrt{a})}$という値になることが分かりました。ここで、ランベルトのW関数が $-\dfrac{1}{e} \leqq x <0$ の範囲では2価関数であることを思い出して下さい。$-\log \sqrt{a}$は常に負なので、$W(x)$の2価関数の定義域内かどうかが重要となります。

$-\dfrac{1}{e} < -\log \sqrt{a} <0$ のとき、$W(-\log \sqrt{a})$は2つの値を同時に与えるため、$e^{-W(-\log \sqrt{a})}$としては2つの値が存在することになります。また、$-\log \sqrt{a}<-\dfrac{1}{e}$ のときは定義域の範囲外なので$W(-\log \sqrt{a})$の値は存在しません。

要するに、放物線と指数関数が第1象限にただ一つの共有点（特にこの場合は接線を共有する点）をもつためには、$e^{-W(-\log \sqrt{a})}$がただ一つの値を取ることが必要となります。$x<0$ の範囲で$W(x)$がただ一つの値を与えるとき、そのような負の$x$の値は$-\dfrac{1}{e}$だけなので、$a$は等式$$-\log \sqrt{a}=-\dfrac{1}{e}$$を満たすことが必要です。これを解いて$$a=e^{\frac{2}{e}}$$を得ます。これこそが求めるべき正の実数$a$の値なのでした。

 

 あとがき

めでたく、放物線 $y=x^2$ に接する指数関数は$$y=e^{\frac{2}{e}x}$$と求められました。冒頭で述べた「$2.087…$くらいの微妙な数」の正体とは、$e^{\frac{2}{e}}$のことです。実際にこの値は$$e^{\frac{2}{e}} \approx 2.0870652286…$$という値をとります。

最後に少しだけ一般化した放物線 $y=px^2$（$p>0$）に接する指数関数を考えてみます。上記の方法で同様に計算すると、そのような指数関数の式は$$y=e^{\frac{2\sqrt{p}}{e}x}$$と求めることができます。

また、$0<a<1$ の範囲では指数関数 $y=a^x$ は $a>1$ の場合と左右対称になるので、$e^{\frac{2}{e}}$の逆数をとれば同様に第2象限で接することが直ちに了解できます。

---

---