正方形に内接する三角形と点の軌跡の長さ（2025年東京大学前期理系数学第1問）

2025年の大学入試2次前期試験が終了しました。受験生の皆様、お疲れ様でした。まずは東京大学の入試問題を取り上げます。

図形の位置関係は次のようになる。

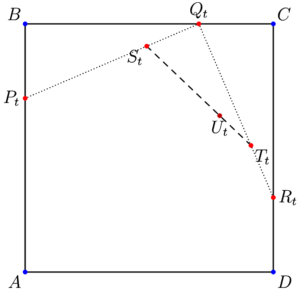
（１）

まず，線分上の内分点を順に求める。

• • 線分 $AB$ 上の点 $P_t$： \[ \begin{aligned}P_t &= \bigl((1-t)\cdot 0 + t\cdot 0,\,(1-t)\cdot 0 + t\cdot 1\bigr) \\ &= (0,t).\end{aligned} \]
  • 線分 $BC$ 上の点 $Q_t$： \[ \begin{aligned}Q_t &= \bigl((1-t)\cdot 0 + t\cdot 1,\,(1-t)\cdot 1 + t\cdot 1\bigr) \\ &= (t,1).\end{aligned} \]
  • 線分 $CD$ 上の点 $R_t$： \[ \begin{aligned}R_t &= \bigl((1-t)\cdot 1 + t\cdot 1,\,(1-t)\cdot 1 + t\cdot 0\bigr) \\ &= (1,\,1-t).\end{aligned} \]

次に，これらを結ぶ線分 $P_tQ_t$，$Q_tR_t$ を比 $t:(1-t)$ で内分する点をそれぞれ $S_t$，$T_t$ とする。

• • 線分 $P_tQ_t$ 上の点 $S_t$： \[ \begin{aligned}S_t &= \bigl((1-t)\cdot 0 + t\cdot t,\,(1-t)\cdot t + t\cdot 1\bigr) \\ &= (t^2,\,2t-t^2).\end{aligned} \]
  • 線分 $Q_tR_t$ 上の点 $T_t$： \[ \begin{aligned}T_t &= \bigl((1-t)\cdot t + t\cdot 1,\,(1-t)\cdot 1 + t\cdot(1-t)\bigr) \\ &= (2t-t^2,\,1-t^2).\end{aligned} \]

最後に，線分 $S_tT_t$ を比 $t:(1-t)$ で内分する点 $U_t$ を求める。 \[ U_t = \bigl((1-t)\,S_t + t\,T_t\bigr). \] すなわち \[ U_t = \Bigl((1-t)\,t^2 + t\,(2t-t^2),\,(1-t)\,(2t-t^2) + t\,(1-t^2)\Bigr). \] 計算すると，$x$-座標は \[ \begin{aligned}(1-t)\,t^2 + t\,(2t-t^2) &= t^2-t^3 + 2t^2-t^3 \\ &= 3t^2-2t^3,\end{aligned} \] $y$-座標は \[ \begin{aligned}(1-t)\,(2t-t^2) + t\,(1-t^2) &= 2t-3t^2 + t^3 + t-t^3 \\ &= 3t-3t^2.\end{aligned} \] よって \[ U_t = \color{red}{\bigl(3t^2-2t^3,\;3t-3t^2\bigr)}. \] さらに $t=0$ のときは $U_0 = A=(0,0)$，$t=1$ のときは $U_1 = D=(1,0)$ となり，問題文の条件と一致する。

（２）

$t$ が $0$ から $1$ へ動くとき，点 $U_t$ はパラメータ表示 \[ x(t) = 3t^2-2t^3, \quad y(t) = 3t-3t^2 \] で与えられる曲線上を動く。これと $x$-軸（線分 $AD$）に囲まれた部分の面積は \[ \text{面積} = \int_{x=0}^{x=1} y\,dx = \int_{t=0}^{t=1} \bigl(3t-3t^2\bigr)\,\frac{dx}{dt}\,dt. \] ここで \[ \frac{dx}{dt} = \frac{d}{dt} \bigl(3t^2-2t^3 \bigr) = 6t-6t^2 = 6t(1-t). \] よって被積分関数は \[ \bigl(3t-3t^2\bigr)\,\bigl(6t-6t^2\bigr) = 18\,t^2(1-t)^2. \] したがって \[ \text{面積} = \int_{0}^{1} 18\,t^2(1-t)^2\,dt. \] 次に \[ \begin{aligned}\int_{0}^{1} t^2(1-t)^2\,dt &= \int_{0}^{1} \bigl(t^2-2t^3 + t^4\bigr)\,dt \\ &= \Bigl[\dfrac{t^3}{3}-\dfrac{2t^4}{4} + \dfrac{t^5}{5}\Bigr]_0^1 \\ &= \dfrac{1}{3}-\dfrac{1}{2} + \dfrac{1}{5} \\ &= \dfrac{10}{30}-\dfrac{15}{30} + \dfrac{6}{30} \\ &= \dfrac{1}{30}.\end{aligned} \] よって \[ \text{面積} = 18 \times \dfrac{1}{30} = \color{red}{\dfrac{3}{5}}. \]

（３）

パラメータ表示 \[ x(t) = 3t^2-2t^3, \quad y(t) = 3t-3t^2 \] において，曲線の長さは \[ L(a) = \int_{t=0}^{t=a} \sqrt{\bigl(x'(t)\bigr)^2 + \bigl(y'(t)\bigr)^2}\,dt. \] まず \[ x'(t) = 6t-6t^2, \quad y'(t) = 3-6t. \] よって \[ \begin{aligned}\bigl(x'(t)\bigr)^2 + \bigl(y'(t)\bigr)^2 &= (6t-6t^2)^2 + (3-6t)^2 \\ &= 36\,t^2(1-t)^2 + 9\,(1-2t)^2.\end{aligned} \] これは \[ 9\Bigl[4\,t^2(1-t)^2 + (1-2t)^2\Bigr]. \] さらに \[ 4\,t^2(1-t)^2 + (1-2t)^2 = (1-2t + 2t^2)^2. \] ($0 \le t \le 1$ の範囲では正なので絶対値は不要) \[ \sqrt{(x'(t))^2 + (y'(t))^2} = 3\bigl(1-2t + 2t^2\bigr). \] よって \[ \begin{aligned}L(a) &= \int_{0}^{a} 3\bigl(1-2t + 2t^2\bigr)\,dt \\ &= 3 \int_{0}^{a} (1-2t + 2t^2)\,dt.\end{aligned} \] カッコ内を積分すると \[ \begin{aligned}\int_{0}^{a} (1-2t + 2t^2)\,dt &= \Bigl[t-t^2 + \dfrac{2}{3}t^3\Bigr]_0^a \\ &= a-a^2 + \dfrac{2}{3}a^3.\end{aligned} \] ゆえに \[ L(a) = 3\Bigl(a-a^2 + \dfrac{2}{3}a^3\Bigr) = \color{red}{3a-3a^2 + 2a^3}. \]

[asy]
import graph;

size(200);

pair A = (0,0), B = (0,1), C = (1,1), D = (1,0);

// パラメータ t の設定
real t = 0.7; // tの値を変更して異なる位置の点を描画可能

// 各分割点の定義
pair P_t = (1-t)*A + t*B;
pair Q_t = (1-t)*B + t*C;
pair R_t = (1-t)*C + t*D;

pair S_t = (1-t)*P_t + t*Q_t;
pair T_t = (1-t)*Q_t + t*R_t;

pair U_t = (1-t)*S_t + t*T_t;

// 四角形 ABCD の描画
draw(A--B--C--D--cycle, gray+linewidth(1.0));

// 分割点の補助線
draw(A--B, solid);
draw(B--C, solid);
draw(C--D, solid);
draw(D--A, solid);
draw(P_t--Q_t, dotted);
draw(Q_t--R_t, dotted);
draw(S_t--T_t, dashed);

// 各点の描画
dot(A, blue);
dot(B, blue);
dot(C, blue);
dot(D, blue);
dot(P_t, red);
dot(Q_t, red);
dot(R_t, red);
dot(S_t, red);
dot(T_t, red);
dot(U_t, heavyred);

// ラベル
label("$A$", A, SW);
label("$B$", B, NW);
label("$C$", C, NE);
label("$D$", D, SE);
label("$P_t$", P_t, W);
label("$Q_t$", Q_t, N);
label("$R_t$", R_t, E);
label("$S_t$", S_t, SW);
label("$T_t$", T_t, SE);
label("$U_t$", U_t, S);
[/asy]