正方形に接する楕円（金沢大学2018年）

解答例

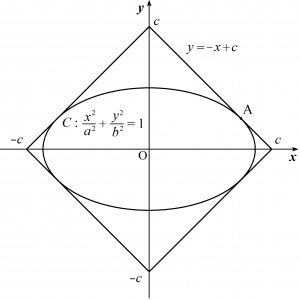
楕円$C$と直線$l$：$y=-x+c$ の接点を$\rm{A}$と置く。$$\dfrac{x^{2}}{a^{2}}+\dfrac{(-x+c)^{2}}{b^{2}}=1$$ $$\therefore b^{2} x^{2}+a^{2}(-x+c)^{2}=a^{2} b^{2}$$ $$\small \therefore \left(a^{2}+b^{2}\right) x^{2}-2 a^{2} c x+\left(a^{2} c^{2}-a^{2} b^{2}\right)=0 \quad \cdots ①$$この判別式を$D$と置くと、$$\small \begin{align} \dfrac{D}{4} &=\left(-a^{2} c\right)^{2}-\left(a^{2}+b^{2}\right)\left(a^{2} c^{2}-a^{2} b^{2}\right) \\ &=a^{4} b^{2}-a^{2} b^{2} c^{2}+a^{2} b^{4} \end{align}$$となる。楕円$C$と直線$l$は接するから、判別式について $D=0$ が成り立つから、$$a^{4} b^{2}-a^{2} b^{2} c^{2}+a^{2} b^{4}=0$$となり、この両辺を$a^{2} b^{2}\,(\ne 0)$で割って$$a^{2}-c^{2}+b^{2}=0$$ $$c^{2}=a^{2}+b^{2} \small{\quad \cdots ②}$$を得る。①を$x$について解くと、$$x=\frac{a^{2} c}{a^{2}+b^{2}}=\frac{a^{2} c}{c^{2}}=\frac{a^{2}}{c}$$ $y=-x+c$ に代入して$$y=-\frac{a^{2}}{c}+c$$よって接点$\rm{A}$の座標は$\left(\dfrac{a^{2}}{c},-\dfrac{a^{2}}{c}+c\right)$と求められる。

ここで②より、$$\begin{aligned} S &=4 \cdot \frac{a^{2}}{c} \cdot\left(-\frac{a^{2}}{c}+c\right) \\ &=\frac{4 a^{2}\left(c^{2}-a^{2}\right)}{c^{2}} \\ &=\frac{4 a^{2} b^{2}}{a^{2}+b^{2}} \end{aligned}$$となり、$$\begin{aligned} T & =4 \int_{0}^{a} \frac{b}{a} \sqrt{a^{2}-x^{2}} d x \\ & =\pi a b \end{aligned}$$と求められる（定積分の値は半径$a$の四分円の面積に等しくなる）。$$\begin{aligned}
\frac{S}{T} &=\dfrac{\dfrac{4 a^{2} b^{2}}{a^{2}+b^{2}}}{\pi a b} \\
&=\dfrac{4 a b}{\pi\left(a^{2}+b^{2}\right)} \\
&=\dfrac{4}{\pi\left(\dfrac{a}{b}+\dfrac{b}{a}\right)} \\
& \leq \dfrac{4}{\pi \cdot 2 \sqrt{\dfrac{a}{b} \cdot \dfrac{b}{a}}}=\dfrac{2}{\pi}
\end{aligned}$$この等号は $\dfrac{a}{b}=\dfrac{b}{a}$ のときに成立する。よって②より、求める等号成立条件は $a=b=\dfrac{c}{\sqrt{2}}$ のときである。