今回は置換積分のテクニック「ワイエルシュトラス置換」について解説します!
ワイエルシュトラス置換とは
「ワイエルシュトラス置換」と聞くと何やら得体の知れないもののような気がしますが、数Ⅲの積分で$$t=\tan \dfrac{x}{2}$$という置き換えをしたことはあるのではないでしょうか。これがワイエルシュトラス置換と呼ばれるものの正体です。
この置換は、三角関数を含む複雑な被積分関数に対して適応すると積分計算が幾分かラクになることが知られています。
$t=\tan \dfrac{x}{2}$ と置くと、$$\sin x=\dfrac{2 t}{1+t^{2}}$$ $$\cos x=\dfrac{1-t^{2}}{1+t^{2}}$$ $$d x=\dfrac{2}{1+t^{2}} d t$$と$t$の有理関数に置き換えることができます。これを証明してみましょう。
変換式の図形的な導出
上記の事実を証明するには、図形的に考えるのが最も見通しが良いでしょう。
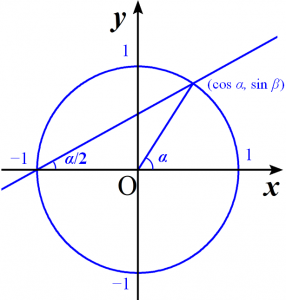
図のように、円 $x^{2}+y^{2}=1$ と点$(-1,0)$を通り傾き $t$ の直線を考えます。この直線と円の$(-1,0)$でない方の交点の座標を$(\cos \alpha, \sin \alpha)$とすると$t=\tan \dfrac{\alpha}{2}$であり、$$\left\{\begin{array}{l}
x^{2}+y^{2}=1 \\
y=t(x+1)
\end{array}\right.$$を連立して$y$を消去すると$$x^{2}+t^{2}(x+1)^{2}=1$$ $$\therefore \left(1+t^{2}\right) x^{2}+2 t^{2} x+t^{2}-1=0$$ $$\therefore (x+1)\left\{\left(1+t^{2}\right) x+\left(t^{2}-1\right)\right\}=0$$と整理できます。ここでは $x \ne -1$ なので$$\left(1+t^{2}\right) x+\left(t^{2}-1\right)=0$$つまり$$x=\dfrac{1-t^{2}}{1+t^{2}}$$となるから、$$\color{red}{\cos \alpha=\dfrac{1-t^{2}}{1+t^{2}}}$$が導かれます。また、このとき $y=\dfrac{2 t}{1+t^{2}}$ となるので、$$\color{red}{\sin \alpha=\dfrac{2 t}{1+t^{2}}}$$が導かれます。
また、$$\dfrac{d t}{d x}=\dfrac{1}{\cos ^{2} \dfrac{x}{2}} \cdot \dfrac{1}{2}$$より、$$\begin{align} \color{red}{d x} &=2 \cos ^{2} \dfrac{x}{2} d t \\ &=\dfrac{2}{1+\tan ^{2} \dfrac{x}{2}} d t \\ &=\color{red}{\dfrac{2}{1+t^{2}} d t} \end{align}$$を得ます。
応用例
以下のような積分にはワイエルシュトラス置換が効きます。答えを覗く前に是非ご自分で解いてみて下さい!
(1)$\displaystyle \int \dfrac{1+ \cos x}{(1+ \sin x )^2} dx$
» (1)の解答例
$\tan \dfrac{x}{2} =t$と置くと、$dx=\dfrac{2}{1+t^2} dt$、$\sin x=\dfrac{2t}{1+t^2}$、$\cos x=\dfrac{1-t^2}{1+t^2}$ であるから、$$\begin{align}& \quad \displaystyle \int \dfrac{1+ \cos x}{(1+ \sin x )^2} dx \\
&=\displaystyle \int \dfrac{1+\dfrac{1-t^2}{1+t^2}}{\left( 1+\dfrac{2t}{1+t^2} \right)^2} \cdot \dfrac{2}{1+t^2} dt \\
&=4\displaystyle \int \dfrac{1}{(1+t)^4} dt \\
&=-\dfrac{4}{3(1+t)^3} +C \\
&=\color{red}{-\dfrac{4}{3\left(1+\tan \dfrac{x}{2}\right)^3} +C} \end{align}$$
» 閉じる
(2)$\displaystyle \int \dfrac{1}{1+ \sin x- \cos x} dx$
» (2)の解答例
$\tan \dfrac{x}{2} =t$と置くと、$dx=\dfrac{2}{1+t^2} dt$、$\sin x=\dfrac{2t}{1+t^2}$、$\cos x=\dfrac{1-t^2}{1+t^2}$ であるから、$$\begin{align}& \ \ \ \ \ \displaystyle \int \dfrac{1}{1+ \sin x- \cos x} dx \\
&=\displaystyle \int \dfrac{1}{1+\dfrac{2t}{1+t^2}-\dfrac{1-t^2}{1+t^2}} \cdot \dfrac{2}{1+t^2} dt \\
&=\displaystyle \int \dfrac{t^2+1}{2t^2+2t} \cdot \dfrac{2}{1+t^2} dt \\
&=\displaystyle \int \dfrac{1}{t(t+1)} dt \\
&=\displaystyle \int \left( \dfrac{1}{t}-\dfrac{1}{t+1} \right) dt \\
&= \log |t|- \log |t+1|+C \\
&= \log \left| \dfrac{t}{t+1}\right|+C \\
&= \color{red}{\log \left| \dfrac{\tan \dfrac{x}{2}}{\tan \dfrac{x}{2} +1}\right|+C} \end{align}$$
» 閉じる
(3)$\displaystyle \int \dfrac{\cos x}{4+5 \sin x} dx$
» (3)の解答例
$\tan \dfrac{x}{2} =t$と置くと、$dx=\dfrac{2}{1+t^2} dt$、$\sin x=\dfrac{2t}{1+t^2}$、$\cos x=\dfrac{1-t^2}{1+t^2}$ であるから、$$\small \begin{align}& \quad \displaystyle \int \dfrac{\cos x}{4+5 \sin x} dx \\
&=\displaystyle \int \dfrac{\dfrac{1-t^2}{1+t^2}}{4+5 \cdot \dfrac{2t}{1+t^2}} \cdot \dfrac{2}{1+t^2} dt \\
&=\displaystyle \int \dfrac{1-t^2}{(1+t^2)(2t+1)(t+2)} dt \end{align}$$と整理できる。ここで恒等式$$\small \dfrac{1-t^2}{(1+t^2)(2t+1)(t+2)}=\dfrac{at+b}{1+t^2}+\dfrac{c}{2t+1}+\dfrac{d}{t+2}$$を解くと、$a=-\dfrac{2}{5}$、$b=0$、$c=\dfrac{2}{5}$、$d=\dfrac{1}{5}$ を得るから、$$\small \begin{align}& \quad \displaystyle \int \dfrac{1-t^2}{(1+t^2)(2t+1)(t+2)} dt \\
&=\dfrac{1}{5} \displaystyle \int \left(-\dfrac{2t}{1+t^2}+\dfrac{2}{2t+1}+\dfrac{1}{t+2}\right) dt \\
&=\dfrac{1}{5} (- \log |1+t^2 |+ \log |2t+1|+ \log |t+2|)+C’ \\
&=\dfrac{1}{5} \log \left| \dfrac{(2t+1)(t+2)}{1+t^2} \right|+C’ \\
&=\dfrac{1}{5} \log \left| \dfrac{2t^2+5t+2}{1+t^2} \right|+C’ \\
&=\dfrac{1}{5} \log \left| \dfrac{5t}{1+t^2}+2 \right|+C’ \\
&=\dfrac{1}{5} \log |\dfrac{1}{2} \left( 5 \cdot \dfrac{2t}{1+t^2}+4 \right)|+C’ \\
&=\dfrac{1}{5} \left( \log |5 \sin x+4|+ \log \dfrac{1}{2} \right)+C’ \\
&=\dfrac{1}{5} \log |5 \sin x+4|+\left( C’+ \log \dfrac{1}{2} \right) \\
&=\color{red}{\dfrac{1}{5} \log |5 \sin x+4|+C} \end{align}$$
〈別解!〉
$$\begin{align}& \ \ \ \ \ \displaystyle \int \dfrac{\cos x}{4+5 \sin x} dx \\
&=\dfrac{1}{5} \displaystyle \int \dfrac{(4+5 \sin x)’}{4+5 \sin x}dx \\
&=\color{red}{\dfrac{1}{5} \log |4+5 \sin x |+C} \end{align}$$
一生懸命置換を使って解いた方は別解を見て落胆したのではないでしょうか(笑)。このように、置換することで却って計算が煩雑になってしまう(もっと簡単な解法を見落としてしまう)ケースもあります。ワイエルシュトラス置換は三角関数を有理関数に変換できる強力な道具ですが、使い所を誤ると自分の首を絞めてしまうので要注意です。
» 閉じる
ワイエルシュトラス置換は便利ですが、計算が簡単にならない場合もあるので、使い所をよく見極めて利用しましょう。$t=\tan \dfrac{x}{2}$ の置換は最終手段として運用するのが良いと思います。

“積分計算の便利ツール「ワイエルシュトラス置換」を使ってみる” への1件の返信