「瞬間部分積分」というのは受験業界で通称されている部分積分の計算法の一種です。使い方によっては計算ミスを減らすことができ、なおかつ計算スピードの向上に繋がるため、数Ⅲ微積で重宝している方も多いのではないでしょうか。今回の記事ではその「瞬間部分積分」の使い方について紹介します!
瞬間部分積分は公式ではない!
一般に、積の形をした関数の部分積分は以下のような表式をもちます。$$\int \color{blue}{f} \color{red}{g}\, \color{black}{d x}=\color{blue}{f} \color{red}{g^{+}}\color{black}{-}\color{blue}{f^{-}} \color{red}{g^{+2}}\color{black}{+}\color{blue}{f^{-2}} \color{red}{g^{+3}}\color{black}{-}\color{blue}{f^{-3}}\color{red}{g^{+4}}\color{black}{+}\cdots$$これは計算すれば自然に得られる式で、公式でも何でもありません。
部分積分の計算は具体的には次のように展開され、最終的に得られる式が上式です。
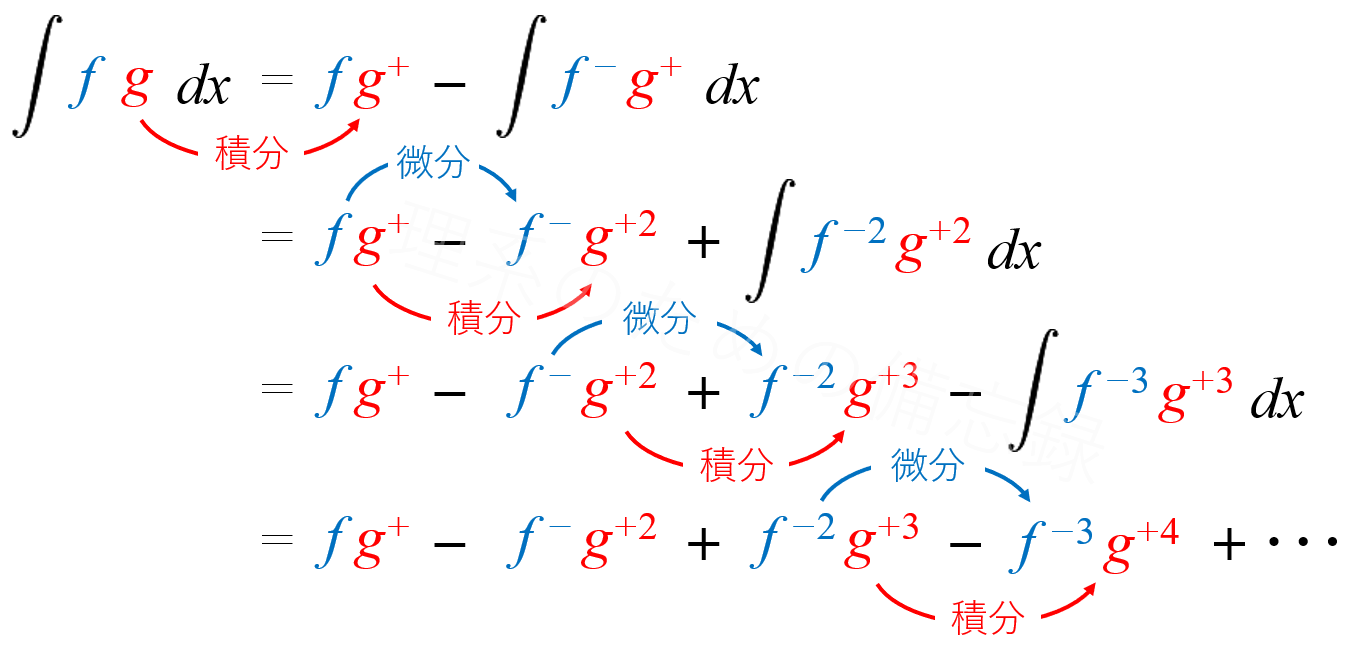
この手続きを簡略化し、機械的に行ってしまおうというのが「瞬間部分積分」のアイデアです。これをまるで公式のように扱う人がいますが、瞬間部分積分はただ単に積分計算の手続きを単純化しているに過ぎないということを覚えておいて下さい。
瞬間部分積分のやり方
それでは、試しに $\displaystyle \int x^{4} e^{x} d x$ という不定積分を求めてみましょう。
最終的に定数になるのは$x^4$の方なので、$x^4$を微分して$e^x$を積分していく方針で瞬間部分積分を使います。$$\begin{array}{c|c|clrr}
+ & \color{blue}{x^{4}} & \color{red}{e^{x}} & \to & x^{4}e^{x} \\
– & \color{blue}{4x^{3}} & \color{red}{e^{x}} & \to & -4x^{3}e^{x} \\
+ & \color{blue}{12 x^{2}} & \color{red}{e^{x}} & \to & 12 x^{2}e^{x} \\
– & \color{blue}{24 x} & \color{red}{e^{x}} & \to & -24 x e^{x} \\
+ & \color{blue}{24} & \color{red}{e^{x}} & \to & 24 e^{x}
\end{array}$$このような表を作って各行の積を取り、各項を加えるだけで不定積分が計算可能です。このとき、左の列の一番上には$+$を書き、$+$と$-$を交互に書いていって下さい。
これで、$$\small \begin{align}
& \quad \int x^{4} e^{x} d x \\ &=\color{blue}{x^{4}}\color{red}{e^{x}}\color{black}{-}\color{blue}{4x^{3}}\color{red}{e^{x}}\color{black}{+}\color{blue}{12 x^{2}}\color{red}{e^{x}}\color{black}{-}\color{blue}{24 x}\color{red}{e^{x}}\color{black}{+}\color{blue}{24}\color{red}{e^{x}}\color{black}{+}C \\
&=\left(x^{4}-4 x^{3}+12 x^{2}-24 x+24\right) e^{x}+C
\end{align}$$と求められます。
同じようにして、不定積分 $\displaystyle \int x^{3} \sin x \, d x$ を求めてみましょう。今回も最終的に定数になるのは$x^3$の方なので、$x^3$を微分して$\sin x$を積分していきます。$$\begin{array}{c|c|clrr}
+ & \color{blue}{x^{3}} & \color{red}{-\cos x} & \to & -x^{3}\cos x \\
– & \color{blue}{3x^{2}} & \color{red}{-\sin x} & \to & 3x^{2}\sin x \\
+ & \color{blue}{6 x} & \color{red}{\cos x} & \to & 6x\cos x \\
– & \color{blue}{6} & \color{red}{\sin x} & \to & -6\sin x
\end{array}$$よって表より、$$\small \begin{align}
& \quad \int x^{3} \sin x \, d x \\ &=\color{blue}{x^{3}}\color{red}{(-\cos x)}\color{black}{-}\color{blue}{3x^{2}}\color{red}{(-\sin x)}\color{black}{+}\color{blue}{6 x}\color{red}{\cos x}\color{black}{-}\color{blue}{6}\color{red}{\sin x}\color{black}{+}C \\
&=-x^{3}\cos x+3x^{2}\sin x+6x\cos x-6\sin x+C
\end{align}$$と求められます。是非、普通の解き方と比べてみて下さい。
対数を含むときは $\log x=t$ と置く!
瞬間部分積分は計算をラクにする便利な方法ですが、対数を含む関数を積分する場合は注意が必要です。
一般に、(多項式)×(対数)型の関数の積分には瞬間部分積分をそのまま適用することはできません。実際にやってみると分かることですが、瞬間部分積分をそのまま適用すると答えが $\small \dfrac{1}{3}x^3\log x-\dfrac{1}{12}x^3+C$ となってしまいます(正しくは $\small \dfrac{1}{3}x^3\log x-\dfrac{1}{9}x^3+C$ です)。こうなってしまう理由は、この方法では $\log x$ を微分すると出てくる$\dfrac{1}{x}$による約分を考慮できていないからです。
これを解決するには $\log x=t$ という置換を考えます。$\log x=t$ と置くと $x=e^{t}$ より、$d x=e^{t} d t$ となるので、被積分関数が($t$の多項式)× $e^t$ の形に直せます。これにより、瞬間部分積分を適用できるようになります。
例えば、不定積分 $\displaystyle \int x(\log x)^{3} d x $ は瞬間部分積分を用いて次のように計算できます。
$\log x=t$ と置くと $x=e^{t}$ より、$d x=e^{t} d t$ となるので、$$\displaystyle \int x(\log x)^{3} d x = \int t^{3} e^{2t} d t$$と変換できます。これに瞬間部分積分を適用すると、$$\begin{array}{c|c|clrr}
+ & \color{blue}{t^{3}} & \color{red}{\dfrac{1}{2}e^{2t}} & \to & \dfrac{1}{2}t^3 e^{2t} \\
– & \color{blue}{3t^{2}} & \color{red}{\dfrac{1}{4}e^{2t}} & \to & -\dfrac{3}{4}t^2 e^{2t} \\
+ & \color{blue}{6 t} & \color{red}{\dfrac{1}{8}e^{2t}} & \to & \dfrac{3}{4}t e^{2t} \\
– & \color{blue}{6} & \color{red}{\dfrac{1}{16}e^{2t}} & \to & -\dfrac{3}{8} e^{2t} \\
\end{array}$$となるので、$$\small \begin{aligned}
& \quad \int x(\log x)^{3} d x \\
&=\int t^{3} e^{2t} d t \\
&=\dfrac{1}{2}t^3 e^{2t}-\dfrac{3}{4}t^2 e^{2t}+\dfrac{3}{4}t e^{2t}-\dfrac{3}{8} e^{2t}+C \\
&=\dfrac{1}{2}x^2(\log x)^3-\dfrac{3}{4}x^2(\log x)^2+\dfrac{3}{4}x^2\log x-\dfrac{3}{8}x^2+C
\end{aligned}$$と求められます。
このように、対数を含む関数の瞬間部分積分は少し面倒ですが、計算ミスを犯す確率はかなり下げられるのではないでしょうか。
(コメント)
以上、瞬間部分積分のやり方について紹介しました。正直に言って、この程度の計算であれば瞬間部分積分に頼らなくても計算できますし、瞬間部分積分の方法でしか部分積分の計算ができないようでは困ります。しかし、この方法だと式を書き下すことなく表を使って計算結果を整理できるので、転記ミスや符号ミスの頻度を格段に減らせます。実際の試験答案に「瞬間部分積分より…」などと書くのは意味不明なので厳禁ですが、不要なケアレスミスを回避するために検算程度には使ってみても良いと思います。

古い記事に対するコメントですみません。
今から15年くらい前にここで取り上げられている「瞬間部分積分」を「テーブル法」という名で普及させようとした者です。
普及活動に携わったと言いつつも、結局、私はきっかけを与えただけで、より適任な方を見つけた後はその方に全てをお任せし、ネットでの普及に目途が着いたのを見届けると同時に、お役目御免と手を引き、以降、海外赴任などもあり、このことは全く忘れてたんです。
そして、コロナ禍の直前に帰国し、「そう言えばテーブル法は普及はどうなってるんだろう」を思い出し、「さぞ日本でも広まっていだろうな」と思いきや、思いの他、広まっておらず、お任せしてた方もその頃までにはネットの世界から姿を消されたご様子でした。
さすがに、日本ではほとんど情報がなかったあの頃と比べれば、現在、この国でも「テーブル法」は多少は知られるようになったみたいですが、それにしても、「テーブル法」についての誤解やデマ(しかも、学校や予備校の先生のようなプロによる)、そして、少し頭を使えばそれらはおかしいと分かるはずなのに、それらを鵜呑みにしてしまう方が多すぎなのは、普及活動に多少なりとも関わった私としては大いに不満です。
こんなことを言うと大袈裟に聞こえて恥ずかしいんですが、私は「テーブル法」の普及活動は、この国の将来に関するある「危惧」に対する使命感から始めたんです。
そして、その後、1、2年の間、他の人から見れば大した事ではないんですが、時間だけは仕事以外の自由詩間の大半を使って、普及活動の準備に費やしていたのです。
なのに、この国での「テーブル法」の普及がしてないどころか、今のこの国を見ていると、私がその時に持っていた「危惧」だけが現実になっていて、本当やるせないと思いで一杯です。
— 「テーブル法」は日本以外の国では、広く知れて、大いに活用されているのですよ。数学で、こんな便利物を使わないじゃ、科学技術立国として、どんどん、他国に置いて行かれますよ。(私の心の中の声)—
今は消滅してしまってるみたいですが、つい最近まで「テーブル法」や「瞬間部分積分」でググると「瞬間部分積分とテーブル法にサヨナラを」という大手予備校の数学講師の方によるブログのエントリが一番に上がっていました。(ちなみに今回「瞬間部分積分」でググるとこのエントリーが5番目に上がってました。)
「テーブル法」の普及がイマイチなのはその予備校の先生のブログエントリーが原因なのではないでしょうか?
まあ、見る人が見れば予備校の講師ともあろう方がこんな記事を書いて恥ずかしくなくないかと思えるようなヨタ記事なんですが、世間では鵜呑みにそれをされている方が多いようです。
(少数意見のようですが、私の気持ちをみごと代弁して下さっているコメントを見かけたのでリンクを貼っておきます。https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12151841497)。
こんな気持ちでずっと悶々としている私ですが、ブログもSNSもしないので、この怒りを、世間に吐き出す場がなく、とりあえず大手書店に行く度、参考書売り場に行って、「テーブル法」が紹介される本がないか確認したり、ネットで年に2、3回、「テーブル法」が普及していないか確認することでお茶を濁してしました。
あっ、どうして、このような古い記事にコメントさせて頂いたかについての説明が長くなり、本題になかなか入れませんね。
要するに本日がその年に数回しかない「テーブル法」の普及度の確認をした日に当たり、そして、偶々、この古い記事に今日はじめて出くわしたのです。
すると、ちゃんと、私が言いたかったことをおっしゃって下さってるし、最近ではめずらしいコメント欄がありましたので、「テーブル法」に対する私の意見を世間の皆様にお聞き頂くいい機会だと思い、お礼かねてコメントさせて頂きます。(ここまでは只の前置きです(汗))
まず、はじめに、「瞬間部分積分は公式ではない!」とことに対して、よくぞおっしゃって下さいました!ありがとうございます。
そうなんです。
日本のネットでは、「テーブル法」について、調べれば簡単にわかることなのに、高校や予備校の先生と言ったプロの方が、この”本質”見ずに、「特殊なケースにしか適用できない裏技、受験テクニック」みたいなものだとか、「『理屈はわからなくてよいから,とにかく覚えろ』と言ってるみたいな”本質”的なないやり方」みたいなことを馬鹿げたことをおっしゃってるのが多すぎるんです。
ここでおっしゃられているように、「テーブル法」の正体は、連続積分に「部分積分の公式」に代入したものを掲載しやすいようにテーブルでまとめただけのものでなんです。
つまり、「部分積分の公式」を使って計算できるものは、「テーブル法」でも全て解けるんです。
日本で「テーブル法」が知られ始めて、もう、かなり立つと思うのですが、未だ、これをググると、次に”log” と出てきて、「テーブル法はlogがあるときは使えない」という記事が多数引っかかります。
出来ますよ。”log” があったって。
「テーブル法」を2回使えばいいんですよ。途中で “f” と “g” を入れ替えて。
学校で、部分積分の公式を使って”log” の付いた計算をする時も、そうするように教わりますよね?
それと同じ要領ですよ。
それだけでなく「テーブル法」を使えば、テーラー展開もフーリエ級数もラプラス変換も部分積分の公式を使った時と同様に解けます。
しかも公式を使った場合よりかなり簡単に「見通し」良く。
ちなみに私が「テーブル法」の普及活動を始めた頃、ネットでは「『テーブル法』を使えばこれらの高度な積分計算がかなりに『見通し良く』できる」と謳ったアメリカ数学協会(MAA)で発表された論文が広く出回っていました。
ついでに言うと、ガンマ関数ももちろん解けます。
これにこついてここで触れるのは、例の「テーブル法」ネガキャンサイトで「『テーブル法』ではこれは解けない」と挑戦されてましたので、私が「簡単に解けますよ」と証拠の動画付きで反論のコメントを送ったのに反映されなかったもので・・・。
また、先のリンクの知恵袋の方もおっしゃってるように、そのネガキャンサイトの先生は、こちらのエントリーの第一段落にあるテーブルを作る前の式を独自に「ブンブン法」と名付け、こちら方が「テーブル法」より何倍も優れていると言い張ってられていました。
でも、「テーブル法」ほ方が「見通し」が良なり、簡単にミスなく計算できるのは明らかですよね?
ちなみに、その記事では「『ブンブン法』では “log” の計算はできない」と言われてました。
「ブンブン法」をテーブル化した「テーブル法」で出来るんだから、ガンバレばできるんじゃないですか?
見るからにややこしそうだからわざわざ確かめてませんが・・・(笑)。
要は「見通し」が悪いから見失われているだけだと思うんですよ。
実は、ネガキャンサイトによる「テーブル法」の批判も、よく読めば、結局はところ、「『たすき掛け』の意味わからない」「テーブルを書くのが面倒くさい」、「鉛筆の芯がもったいない」と数学的本質とは全く関係ないことばかりで、「テーブル法」がもたらす「見通し良さ」に考えれば、本当に、取るに足らないことだと思います。
私に言わせれば、「四則演算」に例えて言えば、言えば「ブンブン法」は「よこの式」で「テーブル法」は「たての式」ですよ。
ちなみに、先に触れたネガキャンサイトが「『テーブル法’』では解けない/手間がかかりすぎる」と挑発してたガンマ関数の問題は、私が調べたところ、2014年の大分大学医学部の3問ある大問の中の3つある小問の結論部分にあたる最後の一問で、試験時間は全体で80分だそうです。
この問題と時間の配分で、進学塾の先生が受験生に、「鉛筆の芯」や「テーブルを書く手間」をケチって、「『”たての式”テーブル法』より『”よこの式”ブンブン法』使え」と受験生に薦めますか?
それと2つ目の『理屈はわからなくてよいから,とにかく覚えろ』というは、ネガキャンブログでも書かれてたんですが、それとは別に、普及活動中にお会いした、”県下一の進学校”(これをやたらこのことを強調されていて、”底辺校出身”の私にはそれだけで不快でした)で”微積”を教えられていると高校の先生にも同じことを言われたんです。
、
そこで、その先生に「先生がおっしゃる『本質』とは何ですか?」と尋ねたら、「それは『入れ子』を次々取り出すようにして答えまでにたどり着くのが醍醐味!」みたいなことを言われたんです。
でも、この様子を「視覚化」しているのが、まさに「テーブル法」そのものではありませんか?そう思いませんか?
このように、「テーブル法」を否定する方は、プロなのに、こちらの管理人さんみたいに「テーブル法」の「本質」を解き明かすようなことはされず、
「私のような『大先生』が今まで知らなかったものを、素人が言って来ても、それは、数学の本質とはかけ離れた。『受験テクニック』のような「邪道」なものに「キワモノ」に違いない」と思われてかのように、決めつけてこられる方が多く、本当に困ったものです。
そして、最近の学生さんも、それを一旦自分で確認するようなことはされず、『大先生』がおっしゃられているから間違いないと「鵜呑み」にされる方が多いようです。
ですので、卑しくプロとあろうという方々が、無責任にそんな誤解やデマを流さないでもらいたいものです。
ちなみに私はその先生と口論になり、やたら、その先生が、自分は”県下一の進学校”の教師で、そこで「微積」を担当するには10年かかると言う事を繰り返されるので、さっき言った理由で癪に障っていたのと、当時、「ゆとり教育」や「大学全入時代」の弊害で、新卒社員の学力の大幅低下が社会問題になりはじめてた頃でもあったため、「県下一の進学校が微積もろくに出来ない卒業生を世に送り出して、社会は迷惑している」みたいなことを言ったら、「私たちも中学から、九九もできない多くの生徒を押し付けられて、をこちらも大変なのよ」と反論され唖然とした覚えがあります。
だって、”県下一の進学校”の理系の教師がこんなこと言うんですよ。「中学を卒業しても九九が出ない生徒が入ってくるって」って。
まあ、いくら、自分や自分が懸命に普及させようとしているものを馬鹿されたため、出た言葉とは言え、その後、その先生は「高校教師というものは世間一般が思うよりはるかにブラックな職業で、授業以外にも、部活で学校がない日も休みが取れない」といった泣き言を続けられたので、私の言ったことは言い過ぎたとは反省はしてるんですが・・・。
でも、当時、第2次安倍政権下での言論統制が厳しかったようで、マスコミも「日本アゲ番組」なんかを盛んに流し、アベノミクス粉飾ためのカモフラージュしていたので、世間では気付いかれている方はあまりいらっしゃらないようでしたが、20世紀「科学技術立国」と鳴らした日本も、欧米先進国はもちろん、アジアの新興国にどんどん追い抜かれて行っている最中でしたから、「将来この国をしょって立とうという”県下一の進学校”に通う学生さんの多くが「九九すらろくに出来ない」と聞くと、日本の『科学技術立国』としての将来も。よいよ真っ暗だな」と「危惧」したことを今でも鮮明に覚えています。
そして、その「危惧」は、この国では現在「現実」になってますよね?
さっきも言ったように、また大袈裟に聞こえちゃいそうで恥ずかしいですが、これも私に「『テーブル法』の普及活動をはじよう」と決心させた「動機」のひとつなんです。
もちろん「テーブル法」の普及だけで、今の日本の「科学技術立国」の凋落が防げたかと言われれば、そうとは思ってませんよ。
ただ、こんな便利な数学のツールが、他国では広く活用されているのに、この国の技術者だけが知らないのでは、他国との競争に大きくマイナスだとは思いました(ちなみに、当時は、ちょうど「機械学習」という言葉が世間で急速に広まり始めた頃でもありました)。
そして、何より、当時はこの国では「日本スゲー」、「日本サイコー」、「世界から憧れられる日本」、「そんな世界の尊敬を集める我が国が他国から学ぶべきことはもはや何ひとつない」みたいな異様な気運が盛り上がっていましたから、それにかまけて、他国の猛追を受けている最中である現実に目を背け、競争を怠り、そして、その結果、今のように落ちぶれてしまわないように、「テーブル法」で「他国にまだ自分たち知らない、自分たちのものより優れたものがたくさんあるんだな。」ということを知ってもらい、それが「この国もまだまだだな」とこの国の技術者をはじめとする多くの方々に考え直してもらえるキッカケ位にはなるんじゃないかと、正直、期待してました。
ちょっと、話を大きくふくらませすぎましたね。お恥ずかしい。
また、いろいろ、思いを吐き出していると長くなりましたね。
まだ。言い足りないんですけれど、これ以上書くと徹夜になりそうなのでこのへんで止めときます。
とにかく、この国でも、多くの方が、デマや誤解を鵜呑みにせず、自らで確かめて、「テーブル法」を便利に使ってくだされば、普及活動に少しでも関わった者しては幸いです。
乱筆、乱文、超長文、失礼しました。
投稿を確認すると、思いのほか、超長文でした。
おゆるし下さいませ。
先日のコメントが反映される確認に来て、もう一度この記事を読み直して気づいたのですが、こちらの「瞬間部分積分法」は私たちが普及させようとしていた「テーブル法」とは違いました。
どちらかというと、こちらのは、「ブンブン法」をテーブル化したものですね?
実は例の「テーブル法にはオサラバ」というエントリーは、著者の大手予備校の先生が有料で自主出版されてるKindle本のPR記事にもなっているのですが、その中で「ブンブン法」をテーブル化した「Superテーブル法Japan」といぅ方法が紹介されているとあります。
私は彼の家計の足しに貢献する気がサラサラないので読んでないのですが、これのことかな?
ちなみに記事によると、その先生は、予備校の授業で「テーブル法」の計算を見せてから「Superテーブル法Japan」を見せると生徒さん達が必ず爆笑させるというのを持ちネタにされてるそうです。
生徒さんの感想に、「そのテーブルの方が部分積分として自然」、「斜めにかけるなんてバカバカしい」とあり、しっくり来なかったんですが、こちらのテーブルをみてピンときた!「甘いわ!」
「テーブル法」で「たすき掛け」をするのにはちゃんと訳があるんですよ、
「テーブル法」は本来は「たすき掛け」だけでなく、実は、最後に「ベルト掛け(?)」(※ 日本の「テーブル」法の紹介記事の多くではこれは省かれてます。)もあり、これがあるから”log” の計算が出来るんです。
よくみると、こちらの”log”の計算は、置換積分してから、テーブルが用いられていますね。
一応、置換せずそのまま「テーブル法」だけで計算してみましたが、解けました。テーブルは3つ必要でしたが…。
「テーブル法」の勝ちじゃないですか?
ホント、彼のネタで爆笑してなんかして、彼の生徒さん、大丈夫なのでしょうか?
記事によると、この話の直後に「テーブル法はアメリカの大学の1,2年向け(日本の高3レベルの微積を扱う — 注. 『ホンマかいな?』 by 日本の高校と米国の大学を卒業した”私” — 教科書のうち,”比較的レベルの低いもの”で扱われている。」とあります。
私が普及活動の準備をしていた当時、”全米第一の名門校”ハーバード大の数学の先生も映画「落ちこぼれの天使たち」のワンシーンのクリップをネットに上げて「テーブル法」普及活動をされてました。
彼が授業で使う自作の微積の教科書には、「テーブル法」についての項目があり、その映画でルー・ダイアモンド・フィリップスの演じる悪ガキの写真付きで、丸一章設けられていました。
当時、ハーバードの数学のランクは世界第2位、対するわれらの”天下”の東大は 30位くらい。
ちなみに、日本に大学にどこも受かった私を拾ってくれたアメリカの州立大学よりやや下、つまり、「ハイテク先進国」と自認していた当時のわが国の最高学府の順位としてかなり心許ないものだと思います。
また、今、最新のを調べたら、ハーバードは5位と少し順位を落としたが、東大は67位と大交替で、欧米の名門校はもちろん、中国(特にこの国の大学は上に10校位います)、香港、シンガポール、サウジ、エジプト、イラン、ベトナム、などアジアの新興国よりの大学よりすっと劣る始末。
(これも当時、私が抱いていた「危惧」のひとつです)
そして、例の生徒さん達も、受かって、いいとこ、その「東大」でしょ?
しかも、まだ、大学生にすらなっていないのに・・・。
記事をまた読み返して、またまた「ブンブン法」と「テーブル法」の違いに気づいたことがあるので書かせて下さい。(度々の自己レス、すみません)
「ブンブン法」の名付け親の予備校の先生(以降、「ブンブン」先生)は「テーブル法」のことを「『学力の低い学生に部分積分を習得させる』のに向いているから(ふむ、ハーバード大の学生がですか?),『理屈はわからなくてよいから,とにかく覚えろ』と指導するわけだ。」と言って批判されているのですが、それって「ブンブン法」の方じゃないですか?
私がこちらの記事のテーブルを見て思うには、「ブンブン法」を使っている人は、繰り返し部分積分の最終結果から、項が進むごとに、「fを微”ブン”」して、gを積”ブン”」して、各項、それらを掛け合わせ、それらをブラマイ交互にして合計するという作業を”機械”的に合計してるだけだと思うのですが、違いますか?
それに対し、「テーブル法」は。「繰り返し部分積分」の”結果”からではなく、「繰り返し部分積分」を”イチ”から計算して、最終的、その結果として、答えを導き出しているんですよ。
つまり、「テーブル法」の”理屈”をちゃんと理解していれば、最終結果の「答え」だけでなく、それに至るまでの「過程」も見えるんです。
これで、どうして、「ブンブン法」に対して、「テーブル法」の方が、『理屈はわからなくてよいから,とにかく覚えろ』と言えるんですか?
実は「テーブル法」の実体は、「繰り返し部分積分」ではなく、「部分積分」をなのです。
具体的にいうと、「テーブル法」が表していすのは、「部分積分の公式」の右辺で、「”ななめ”掛け」の部分はその第1項で、「”よこ”掛け」は第2項 にあたります。 (※)
そして、「繰り返し部分積分」の計算に「テーブル法」を使うときは、「”よこ”掛け」で求まる第2項目の積分式に、部分積分の公式の「テーブル」を”入れ子”にすることを繰り返すのです。
「ブンブン先生」と同じように「テーブル法」について、「『理屈はいいから,とにかく覚えろ』みたいなやり方は相手にされないですよね」と鼻で笑った県下一の進学校の微積の先生、
そういうあなたに「ちゃんと調べてからモノを言って下さい」と私が抗議すると、あなたは「テーブル法」についてちゃんと検討して、その”本質”」まで、ちゃんと理解した上で批判している」と繰り返し言われてましたね?
それなのに、あなたが、繰り返し部分積分の問題では、生徒さんたちに「『入れ子人形』を次々入れて行って、最後に答えにたどり着く、”醍醐味”を味わって欲しい」みたなことを言われたの聞き、私が激怒した理由はこれでおわかりですよね?
それと、「”ななめ”にかけるなんてバカバカしい」と言っていたブンブン先生の生徒さんも、わかりましたか?
「テーブル法」の”ななめ”にはちゃんと意味があるのです。
「テーブル法」は本来は「”ななめ”掛け」と「”よこ”掛け」からなっているのです。
「テーブル法」が「”ななめ”掛け」だけに見えるのは、「”よこ”掛け」は、”よこ”に”掛け”でできた”合成”関数なので、 その積分式は「部分積分の公式」で「入れ子」に出来るから、”よこ”が消えて、”ななめ”だけが残っているんです。
だから、ここは、本来、「『”よこ”掛け』しかない『ブンブン法』は、『部分積分の公式』の第2項目の積分部分はどうなっているのか?」という方を考えなければならないところ。
ちなみに、この答えについては、調べましたから、知ってる方も、ここで、私に教えていただかなくて結構です(あとで、ツッコミに使いますので・・・(笑))。
そして、「テーブル法」は 「fが最終的に ゼロ (”0″)になる場合でないと使えない」とか、「関数にlog が含まれる場合も使えない」という、”デマ” を信じてられている方も、そういう場合はどうするればいいかわかりますか?
そう、「よこ掛け」して、第二項目積分式を導き、それを解いていけばいいです。
私はこれで、この記事の log を含む関数を積分する問題を、t = log x に代入することなしね(この考え自体は、物理とかでも重要なので覚えてといて、学生さんは損はないと思います)、「テーブル法」だけで、3度の「入れ子」を使って答えを導きました(「ななめ」にこだわる方は「ななめ」4回で解けます)。
ここまで、書いて、「瞬間部分積分とテーブル法にサヨナラを」という記事で(※2)、「ブンブン」先生がご自身が、「被積分関数に対数関数が入っているときは”ブンブン”できない」と認められているですが、これって、本当かなと思ったんです。
そこで、さっきも予告したように、「『ブンブン法』では、「部分積分の公式」の第2項目の積分部分はどうなってるのか」について調べてみました。
そして、やっぱり、「『ブンブン法』の方こそ、『理屈はわからなくてよいから,とにかく覚えろ』」と確信したのですが、これを書き出すとまた、長くなりそうなので、気付けば、また、深夜も超えてしまったということもありますし、次回にします(ご迷惑でなければですが・・・)。
ではおやすみなさい。
※1. これに関しましては、石村園子先生著の「よくわかる微分積分」に、「部分積分の公式」の覚え方として、これを「うまい方法デ~ス」と紹介されています。
※2. ずっと、言い忘れてましたが、この記事でいう”瞬間部分積分”は「デーブル法」や「ブンブン法」とは全く別物です。
>>「”よこ”掛け」は、”よこ”に”掛け”でできた”合成”関数なので
日本語で”合成関数”と言ったら全く別の意味ですね。
「”積” の”関数”」というべきでした。
それと、t=log x についても 私は e^ln(x) = x のつもりで発言しました。
それで、なぜ、そうなるか度忘れしてたので、Youtube の動画で対数の復習をしていたら、その動画の先生が(調べてみると、偶々予備校の先生で、しかも、「ブンブン」先生と同じ予備校の。こちらの方のほうが、当然ながら、有名みたいですが…。) が、私が前回、「テーブル」法を普及させようと決意した理由で”膨らませすぎた”言ったものと、同じ理由で動画を公開されてると言われてました(https://www.youtube.com/watch?v=RWQi2uOoHsQ&t=119s)。
私と同じ気持ちの方、おられたんだな…。
動画の先生も「ガラにもない事」と言われていますが、私のような「危惧」を持っている方は、本当に多い思います(実際、その「危惧」が、この国は今、「現実」になってますし・・・)。
大学も推薦入学で優秀な生徒さんを引き付けるより、授業料免除とかすればいいのに。
もしくは、アメリカ のように、入学は「緩く」(と昔から言われてましたが、「大学全入」時代で、推薦が50%以上になったこの国の大学入試では「緩さ」はもうあまり変わらない気がする)てもいいけど、卒業も同じように厳しくして、もっと、学生に勉強させないと、国際競争に付いていけないような気がします。
また、私は、以前「”元祖”瞬間部分積分法」の予備校の先生に「ブンブン先生」の記事に反撃するようお願いしたのですが、
当時、この国では「日本スゲー」病が蔓延していて、その先生もその病気に侵されていたのか「日本が海外に学ぶべきことなど、もはや何一つない」と言わんばかりに、「テーブル法」について全く見向きもして下さらなかったので、「日本の予備校の先生なんて、もうそんなに偉くない!」という意味で私がその先生に言っていたのと全く同じことが、動画では言われてます。
ちなみに、私が「東大」のランキングについて調べたのは、この先生が「東大、京大の入学指導には定評がある」みたいなことをプロフィールに書かれていたからです。
今、進学塾の先生に求められているのは、それでないですよね?
それより、私のように学力の低い学生さんの能力を引き上げることの方が彼らに求められていることだと思うんです?
そもそも、偏差値の高い頭のいい学生さんは、みんな、受験勉強に青春を捧げるより、推薦で入りますよね。
当時は、「東大」は 「総合的」には「昔の名前」でアジア1、2位で、世界30位でしたが(最新のは90位)、工学、農業系のランクでは、もうすでに、最新の数学のものと同じような”悲惨”な状態でした。
ついでに言うと、それ、プラス、韓国、台湾、インド、マレーシア、パキスタンが上にいました — 逆に、初めの3国が最新の数学のランキングで上位に入っていなかったことに驚いた—。
ちなみに、当時、日本のマスコミは、「日本の家電大好き芸人」さんが頻繁にテレビに出したりして、まだまだ、この国を「世界のハイテク家電大国」みたいに報道していました。
ワイドショーや報道バラエティー番組では「日本のハイテク製品を求めて中国からの爆買いの波が押し寄せている」と盛んに報道されていました。
しかし、私が見る限り、当時、中国の方が押し寄せていたのは 日本の『家電量販店』ではなく『ドラックストア』でした(笑)。
ついでにいうと、もうすでに、その当時で、世界工学系大学のランクのベスト3は、MIT、カルテック、スタンフォード、ケンブリッジ、オックスフォードの米英の名門大学ではなく、1位が中国の清華大学、2、3位が、シンガポールの南洋理工大学とシンガポール国立大学 でした。
ちなみに、南洋理工大学からは、ある夏、何人か、私がいたアメリカの大学に交換留学にされて来て、日本人をいると聞き、私をところに訪ねて来て下さいました。
そして、「日本はアジア唯一の先進国で、私たち国民すべての憧れで、お手本です。私たちも一生懸命努力して、いつかはあなたたちのような立派な工業立国になりたいです。」とわざわざそれだけを言われてました。
私は、「いや、今は偶々、同じ学校にいるけれど、私はあなたたちと違ってエリートどころか、底辺校出身の落ちこぼれなんですけれど…」と言っても、「そんなの関係ない」と言って下さって、妙に恐縮した覚えがあります。
そんな彼らは完全に我々を追い抜き、ホンマ、頑張りすぎやで…(汗)。
ちなみに、最新のランキングでは、ベスト10 は、1位が清華大学、2位の南洋理工大学は変わりませんが、シンガポールの2校と香港の1校を除いて、後はすべて中国の大学で、やっとMITが11位に入ってます。
わが東大はソウル大学とタイの77位。
と言っても、安部政権のメディアコントール下のマスコミの忖度報道に踊らされて日韓半導体問題の時、「韓国に勝ったー」と叫んでいた方、お待ち下さい。
韓国では、他に延世大学が56位に入っています。
とにかく、当時でもうすでにそんな状態だったのに、日本の報道バラエティーやワイドショー番組では「中国製品は粗悪品ばかり」、「中国の軍事兵器は時代遅れで、日本の最新の兵器には太刀打ちできない」みたいなことが盛んに言われました。
このことを指摘して、「”元祖”瞬間部分積分法」の先生に、「テーブル法」の普及をお願いしたのに、その予備校先生には、全く、響かなかったみたいで、最終的には、やっとお返事を頂けましたが、動画の先生とは違ってそういうことを全く理解されてないというか…。
その先生は、予備校数学界ではそれなりの地位にいる先生だと聞いてましたので、「何だかな~」とこの国の将来にひどく絶望した記憶があります。(そして、何度も言いますが、私がお伝えした「危惧」通りにいまこの国はなってます)。
これで思い出したのですが、話は逸れますが、日本で「テーブル法」についてデマや誤解とともに、私が日本のネットとメディアを見てずっとイラっと来てて、みなさん聞いてもらいたいことがあるので、少し言わせて下さい。
最近の日本のメディアの方は、「権力の監視機関」どころか、権力にこびてホント質がかなり落ちたと思いますが、それだけではなく、世界の常識を知らなすぎます。
私が唯一見てる日本のサイト、「日刊ゲンダイDIGITA」では毎日のように、皇室の方の進路について連日報道されているのですが(動画の先生のご意見との関連はここです(笑))、
以前、その方のお義兄様が「法学部しか出てないのにアメリカのロースクールに入学できたのは『皇室特権』を使ったからに違いない!」と、日本のマスコミに酷いバッシングされていたのですが、この日本のメディアの発言は”アホ”すぎます。
なぜなら、アメリカの学部には、’法学部」はないからです(こんなの”常識”です)。
向こうのロースクールは大学の4年生の過程を終了していればどんな学部からでも入れます(メディカルスクールもです!)。
日本でも、無敵の美人刑事弁護人で有名な方は、文学部出身だと言われてましたよ。
バッシングしておきながら、日本のメディアのこの発言は恥ずかしすぎます。
また、以前、問題発言をされた経済学者の先生を、未だなお”世界が認めた天才イェール大学教授” と日本のメディアはもてはやしていますよね?
アメリカの大学を出た私に言わせれば、アメリカ大学で助教授を10年近くしてる人を”イェール大学教授”というのは、”東大を受験しただけ”の人を「東大生」と言ってるのと同じです。
普通、5年して准教授に出世できなければその人の大学でキャリアは終わってます。
これって、アメリカの大学を出た人にすれば、は常識だと思いますよ。
ちなみに、問題発言を受けて書かれたNYタイムズの彼についての記事では「アメリカの学会では全く”無名”」と書かれてます。
これで、「肩書」につられて、日本のメディアはスゴイ人にしてしまうんだから、都知事もカイロ大卒を言いたがる訳です。
それと、私が日本に帰ってきて、日本のメディアについて、一番、「ダメ」だと思い、腹が立つことは、「メディアの世界を生活の糧にしているのに、『表現の自由』が憲法に明記された基本的”人権”で、『民主主義の根本』だということを理解してない」ことです。
日本のメディアは「SNSによる誹謗中傷は犯罪です」とよく喚きますが。「名誉棄損」による刑事罰は国連人権委員会が廃止を勧告していて、すでに世界の多くで廃止されています。
ちなみに、日本のメディアはなぜ、「SNSの誹謗中傷」とだけ、言うのでしょう。
影響力を考えれば、「メディアでの誹謗中傷」の方がもっと問題だと思うんですが…。
とにかく、日本のマスコミは、これを、SNS、ネット叩きに利用して、恥ずかしくないんでしょうか?
ちなみに、私はSNSは全くしてません。
それでも、今の日本のSNS、ネット叩きにはホントに頭に来てます。
権力にはヘコヘコしてるくせに、一般庶民にのような弱者は、メディアの力を使って徹底的に追い詰める。
とくに、放送関係のメディアって、国民から電波をお預かりして、放送させてもらっている立場でしょ?
本来の使命である「権力の監視」は出来なくせに、国民とか、力の弱い人たちを徹底的に叩きまくる、ホント、サイテーです。
それと東社長の「誹謗中傷にも言論の自由」という発言を日本のメディアは叩いていますが、これは世界では正論ですよ。
ちなみに、私はジャニーズファンでなく、どちらというと、アンチです。、
アメリカの有名な判例で、「合衆国憲法修正第1条の『言論/表現の自由』は、社会的弱者が、社会的に”不人気”な発言をしても、国や権力者から社会的、経済的制裁を受けないことを保証している」とあるんです。
アメリカでも弁護士資格をもち、帰国子女でもある山口貴士弁護士も「表現の自由は、多数派の幸福のためではなく、多数派から支持されない、あるいは、嫌われる表現を守るためにこそ存在します。」とつぶやかれてます。
そして、山口先生も言われてますが、こんなのは、今の日本以外の国では「基本中の基本」なのです。
それを、この国では、メディアや、しかも、リベラルまでもが、SNS、ネット叩きをして、規制や厳罰化まで煽るなんて!
アメリカでも、事実に基づかないデマなどの「中傷」は罰せられますよ。でも、事実に基づくことや、意見、批判は全く問題ありません。
なのに、今の日本のメディアは、事実に基づくことでも、自分たちに気にくわないは全て「誹謗中傷」と言います。
でも、これは昔、「バッシング」と言って、世間がそんな発言をしても、何も問題ありませんでしたよね?
最近見た記事で、野球で調子が悪い選手を「疫病神」と言っただけで、それをさも「犯罪」のように書いてた日本のメディアの記事を見た。
その記事だと、球団はそれに対して法的手段を取るかもしれないと示唆していた。
もし、そうしたら、もう誰も野球を応援しなくなるのではないですか。
私は、東京オリンピックで、「SNSを訴える」とか聞いて、大谷選手以外に日本のスポーツを応援するのを止めました。
東京も、今回のも、オリンピックは全く見なかった。
それはさておき、野球の件に話を戻すと、そう、言われるのは、その選手の不甲斐なさが原因ですよね。
そのくらい活躍して、野球の実力で黙らせればいいと思います。
ホント、何でも、自分が気に喰わないことは、「誹謗中傷」と言って、世論操作までして、庶民の口を塞ごうとするメディア関係者って、こんなの許されていいのですか?
メディアの、こういう影響力を使った世論操作は、アメリカでは、違法だし、庶民に対する「言論の自由」という「人権」の侵害ですよ。
また、日本のメディアは、昔は、評価、論評やバッシングと言われていたものを、わざわざ「誹謗中傷」と言って、「中傷」と違い、「事実に基づく」ことでもメディアが自分たちの「気に入らない」言論なら何でも「犯罪」にできるみたいに言ってますが、ちゃんと「誹謗中傷」という意味を辞書で調べて下さい。
これも、「中傷」と同じように「”事実に基づかない”批判」と書いてありますよ。
そもそも、「事実に基づく」批判でも訴えられる日本の「侮辱罪」は国連人権委員会で廃止するよう勧告されています。
韓国では、「フェリー沈没」事件の際、産経のソウル支局長が逮捕された事件が世界的にも問題になった際、人権団体が、韓国の「名誉棄損罪」と「侮辱罪」が人権違反だと、国連に訴えて、国連によるそれらの非難声明を引き出しているのです。
(ちなみに、これらの法律と、日本の「名誉棄損罪」と「侮辱罪」は英文で読む限り、ほぼ同じですが、韓国のメディアによると、こんな「人権侵害」の法律がある国は、民主国家では他にないそうです)・
こんなに、日本とも関りが深い事なのに、日本のメディアがこれを報道せず、「SNSの誹謗中傷は犯罪だ!」とばかり報道することについて皆さんはどう思われます?(私はメディアに対して、「憤り」を覚えます。)
また、韓国はこの国連からこの声明を引き出すのに、国際的な人権団体のヒューマン・ライツ・ウォッチの協力を得たのですが、私もその日本支部に「『侮辱罪の厳罰化』や 「SNSの誹謗中傷」報道で、日本のメディアはがおかしくないか?」と連絡をとったんですが、完全に無視されました。
調べてみると、案の定、日本支部の役員は、メディア関係者ばかり。
HRWの本部は知っているのかな?
みなさん、これについてもどう思います?
それと、本来、「公人」が「私人」を訴える場合、より高いハードルがあるのですが、この国の「SNS誹謗中傷」裁判では、著名人が一般人をバンバン訴えて、勝ってますよね。
こんなのアメリカでは考えられない。
そもそも、日本では、芸能人とかが、自分たちは「私人」だとか言うじゃないですか…。
裁判での「公人」は、英語の訳は”public servant” ではなく、”public figure” で、「公的な機関に勤めている人」ではなく、政治家はもちろん、芸能人やスポーツ選手など、「社会的発言力、影響力が強い」著名人のことを言うはずですよね?
日本でも「みなし公人/準公人」という言葉があると聞きましたよ。
メディアの偏向報道によって、完全に日本の法律が捻じ曲げられてますよ。
だから、最近、世間を騒がしているフワちゃんさんの事件もそう。
ちゃんと謝罪したなら、世間もこれ以上、彼女に制裁を与える必要ないと思います。
メディアはこの件を騒ぐことによって、SNS上での一般庶民による言論の「言葉狩り」、もしくは、フジTVが「テラハ」事件の時、または、日テレが「セクシー田中さん」事件の時にしたように、自分たちの対する批判が起こった時、SNSを叩きで、視聴者に責任を押し付け、それをかわすのに利用しようと企んでいるのがミエミエだと思います。
実際、彼女は、芸能事務所に属さないフリーの方なんでしょ? また、”弱者”叩きかよ。日本のマスコミは…。
大体、『表現の不自由』の批判と戦っている津田大介さんがSNSでの「誹謗中傷」叩きに精を出されてるなんて、ホント、今の日本のメディアやリベラルは、お子ちゃまというか、幼稚性には頭を抱えます。
そういえば、何かのネット動画で見たんですが、弁護士の三輪記子先生が、「メディアに携わるものは、『誹謗中傷』と言われるような『言論』による攻撃でも、それを『裁判』とかではなく、『言論』で言い返すべき」みたいなことを言われてて、「私もアンチにどんな酷い事を言われても彼らの『言論の自由』を尊重してる」と言った上で「その代わり私も言い返すから」と言われ、日本にも、ようやく、こんな大人で、かっこいいことをおっしゃるメディア関係者が出てきたかと感心しました。
ちなみに、その隣で、官房長官会見で、当時の松野官房長官に、ジャニオタの方による「SNS誹謗中傷」問題で、国連人権委員会から「廃止」が勧告されている「侮辱罪」の更なる「厳罰化」を要求した望月衣塑子東京新聞記者が気まずそうにされていました。
今、思い出しましたが、先の三輪記子先生の発言を、アメリカで「SNSでの脅迫」が罪に問えるかが争点になったデロニス裁判で、無罪を下した連邦最高裁判所の「ある言論が気に入らなければ言論でやり返せ。ただし政府はそれを禁じることはできない、」と声明をさされたのですが、それと同じですね。
それと、アメリカ大使館の公式マガジン「アメリカン・ビュー」の「言論の自由は誰もが有する権利」という記事の中でも、「言論の自由という名の下に不快で耐え難い意見が表明されたとしても、我々は同じ権利を行使し、討論や平和的な抗議行動を通じて異論を述べることができる。」とありました。
また、この記事には「表現の自由は、”世界人権宣言”(”!”)にうたわれるとおり、すべての人が有する権利であり、インターネット上での発言も含まれる。」とありました。
つまり、日本のメディアは、すげ、自分たちに対する批判を「人格攻撃」などと言い換えて、さも、「表現の自由」を価値の低い人権やあるいは人権でないかのように、その価値を貶めるような印象操作をしてますが、世界ではそんな”軽い”ものではなく、「民主主義の根本」とみなされているとても尊重されているものなのです。
また、「言論の自由」は「すべての人が有する権利」で、正式な訓練を受けた「メディア関係」にだけ許されている権利ではありません。(とくに、未熟な最近の日本のメディア関係者にそんなことは言われたくありません)。
そして、この記事はアメリカの社会改革論者で奴隷制度廃止を訴えたフレデリック・ダグラスは次のような言葉で占められています。
「自らの考えや意見を述べる権利がなくなってしまったとき、自由は無意味である。これこそ、すべての権利の中で暴君が最も恐れているものだ。言論の自由の抑圧は二重の意味で悪行である。話し手の権利だけでなく聞き手の権利も侵害するからだ」
日本のメディアは何を恐れているんでしょうねぇ?
とにかく、私はこの記事を読む度に、一般人によるSNS叩きに目くじらを立てている最近の日本のメディアはカッコ悪いばかりか、有害だと常に思うんです。
昔は、メディアの人って、反権力でカッコよく、私たち庶民のあこがれの職業でした。
そして、犯罪者でもない一般視聴者、読者に噛みつくなんてみっともないことはしなかった。
やっぱり、斜陽産業なんだな…(と言いつつ、この国全体が、斜陽国になってますが…)。
あっ、それと、最近、芸能人やメディア関係者は、視聴者に対して「匿名は卑怯」なんて、一昔前なら、「それも視聴者の権利なんだから」と「みっともないから止めなさい」同僚、共演者に言われ、止められたことを、恥ずかし気もなく言って、すげ、視聴者の口を塞ごうとしますよね?
こんなの「世間に与える影響力」を考えれば、一般「庶民」のメディア関係への「匿名」の意見が「卑怯」でもなんでもないのは分かり切っているじゃないですか?
実際、一昔前はこういう意見は、『強者の論理』と言って、一蹴されたものです。
そもそも、アメリカでネットが始まったころは、ネットは「匿名」でするのが原則ですからね(映画「ユー・ガット・メール」を御覧になって下さいよ)。
大体、ネット後進国のネット後進業界(Hulu や Netflix がアメリカで人気になってから、この国で、TVer みたいなサービスが広まるまで何年かかったのですか?)の日本のメディア界が、ネットの世界のルールを自分に都合よく書き換えようなんて、アメリカで情報スーパーハイウェイ構想が始まったころから、ネットをしてた私に言わせると「ふざけるな」という話です。
他にも、日本のメディアは、SNS上で痛ましい事件が起こる度「投稿を削除するのは卑怯だ」なんていう発言しますよね。
これって、、ナチスのプロパガンダ相、ゲッペロス が使ったプロパガンダと全く同じなんですよ。
これを誰も指摘しないのはホントにこの国はおかしい。
神戸のパワハラ事件で亡くなられた県幹部職員の方も、マスコミがSNS叩きで作り出したこんな世間の風潮の犠牲になったと言っても過言ではないと私は思います。
なぜなら、以前のマスコミなら、お亡くなりなられるより、もっと、前に、匿名通報妨害について騒いでいたでしょうし。)
そもそも、(事実に基づかないものでもない)、オンライン・インサルトが十二分に『言論の自由』の範囲内なんて世界の常識ですよ
「Japan Today」なんかで、英語圏の方の意見なんか見てると、こういう意見が飛び交っていますし、日本のメディアによるこの国のSNS叩きを見て「ホント、日本は”落ち目”だな」と笑われています。
名誉棄損なんて、影響力を持つ人が、メディアや出版物を通して行ったものが裁かれるのであって、どこの馬の骨とも知れない匿名のつぶやきなんて司法が裁く対象になりえない。
国連に「言論弾圧」国とされた韓国ですら、「世間一般に広まったこと」を基準にしている。日本みたいに「多くの人に目にさらられる状態」にあっただけで、名誉棄損の対象にしてるおかしな国は他にあるんですか?
こういことも、自分たちのSNS叩きに都合が悪いからマスコミが報道しないから世間のみなさん、ご存じないでしょ?
それと、名誉棄損で情報開示請求だって、中学でも習うくらいの知識から言っても「違憲」でしょ?
そもそも、「名誉」権なんか、憲法に書いてるのですか?
こんなものだけで、憲法に明示されている、「言論の自由」、「通信の秘密」、「公平な裁判を受ける権利」(※)という国民の人権を裁判所が侵害してもいいのですか?
なんか、日本の裁判所は「名誉」権を「幸福追求権」と解釈して、「それが何よりも重んじられる」という部分を無理やりこじつけて、「『名誉』が『言論の自由』より上」と解釈してるそうですが、司法がこういう判断している民主国家は、この国の他では、国連が言論弾圧を非難している韓国くらいだそうです。
ホント、日本国憲法になってもう80年以上もたつのに、未だ人権感覚は未熟みたいですね。
また、日本の裁判所は『フライバシー権』も、『幸福追求権』と解釈してるそうですね?
情報開示請求なんて完全な「フライバシー侵害」なんだから、ぶつかったら、「名誉権」の優位性はキャンセルされて、情報開示請求なんて正当化できないだなんて、中学生でもわかることでしょ?
なのに、裁判所があんなに簡単に情報開示を認めまくっているのおかしいでしょ?
実際、情報開示された方が裁判に勝つケースが、ネットでいろいろ公開されてますよ。
こんな、重大な人権侵害の誤りを犯しておいて、情報開示を許可した裁判官は処分されないんですか?
「プライバシー侵害」みたいな重大な人権侵害を犯していて、「すまん、間違えた」だけで済むわけないじゃないですか?
ちなみに、そう、言ってアメリカの裁判では、情報開示請求が却下されてました。
なのに、日本の裁判者は謝罪すらしないんでしょ?酷すぎます。
メディアはなぜこれをもっと、追求しないんだ。
ここまで言って、ジャニーズの件を話していたことを思い出したのですが(笑)、メディアが、東社長を叩いて、堂本剛さんを持ち上てるのもおかしいですよね?
だって、堂本さんは、事件を放置した東さんにも責任もあるって批判されてますが、それなら、堂本さんもでしょ?
私は昔からジャニー氏がそういうことをしてたということは噂で聞いて、アンチですから、それを信じてましたが、それでも、堂本さんが、彼が番組で「今日、ジャニーさんに”You”って呼ばれてた」と盛んにアピールしてたから、私も危うく「ジャニー氏も世間で言われる悪い人ではなく、実際、会ったら、案外、気のいいおじさんかも」と騙されそうになりました。
そして、「誹謗中傷」してるジャニオタの人も、堂本さんのそういう発言を信じて、ジャニー氏のことを悪く言う人たちを「誹謗中傷」するようになったのではないですか?
だから、東さんに責任があるのなら、堂本さんも同じ。
それなら、自分も事務所に残って、被害者の方への保証のために働くべき。
なんで、何も関係のない、なにわ男子が稼いだお金が保証に使われなければならないんですか?
そして、堂本さんは、可愛い奥さんをもらって、自分は逃げている場合なんですか?
それと、玉川徹さんも、東社長やジャニオタの方を批判したと聞きましたが、その堂本さんの番組を放送してのはテレ朝でしたよ。
あなたの局が、ジャニオタの方々がSNSで「誹謗中傷」する原因を作ったんじゃないですか?
それに、玉川さんのワイドショー番組って、ジャニーズ問題をいち早く追及しようとした梨本勝さんをTV界から追放した番組ですよね。
天国の梨本さんに謝罪も済ませないで、何を自分だけカッコつけているのでしょうか?
この人、Ryuchellさんの痛ましい事件の時も、全く関係ないのに、無理矢理、それに託けて、SNS、ネット叩きをしてましたよね。
はっきり言って、卑怯なのは、メディアの力を使って、「SNSユーザーは卑怯だ」と印象操作している玉川さんの方でだし、彼のしたことは、完全に、Ryuchellさんと一般視聴者に対する人権侵害だと思います。
それと、実際、小林よしのりさんが、「わしがおまえらを誹謗中傷してると言ってるそうだな」と言って押しかけても、玉川さんは逃げ回っているそうじゃないですか?
「匿名」でSNSしてる方が、名乗り出て、その人が、弱い人なら強く出て、影響力が強い人なら逃げるんでしょ?
実際、大阪の知事に酷い事を言われても、問題発言で干された時も何も出来なかったでしょ?
それを相手が一般視聴者なら強気になって、メディアの力を使って、SNS叩きでとことん追い詰める、「卑怯」ってこういうことを言うんですよ。
とにかく、メディアを使って、「誹謗中傷は犯罪です」なんて言ってるのは、憲法違反で、国民に対する人権侵害なんですよ。
人質司法のこともそうですが、ホント、裁判所と法律家の方はしっかりしてほしいです。
何か、国連の人権委員の方々が日本に調査に来たのは、ジャニーズ問題ためみたいに、メディアは言ってますけれど、彼らは、この国の人権で様々な人権侵害が蔓延っていることに調査に来て、ジュニーズ問題はその一部なんでしょ?
実際、人質司法で、情報開示請求同様、違憲なのに、令状を出しまくってことで、裁判所も、勧告をされたと聞きましたよ。
こういう肝心なことは、日本のメディアは、SNS叩きに都合が悪いからか、一切、報じないのはなぜなんですかねぇ。
ああ、話が逸れすぎて、すみません。
「侮辱罪の厳罰化」問題って、あったじゃないですか?
これもアメリカから帰国したばかりだった私には、メディアやリベラルが反対の声を上げなかったの不思議で、
さっきも、HRWに連絡したと言いましたが、いろいろメディアに連絡したのですが、最後の最後で、アリバイ作り程度に声を上げて下さった以外、(『赤旗』さん以外には)完全に無視されたんです。
そして、日本のメディアは「言論の自由」を守るため、「侮辱罪の厳罰化」について「非難」の声をあげるどころか、「厳罰化」に賛成し、それを煽るような報道ばかりされたてましたよね。
そういう、プロとしての使命を果たさないどころか、こんな恥ずかしいことを平気でする点で、私にとっては「テーブル法」の件と同列の問題だったもので…。
今日は、なぜ、「ブンブン法」では”log”がついた計算ができない(“?”)か、それは「ブンブン法」の方が、「理屈はいいから、とにかく覚えろ」だからについて言うつもりでしたね。
今回も、気が付いたら徹夜してましたし、もう休みが終わって時間がないので、これについて、わたしの話を下さる方は、リクエストください。
特に、「ブンブン先生」による陥れられた「テーブル法」に対する「冤罪」を晴らす記事を書いて下さる数学系ブログをされている方からだと本当にありがたいです。
そして、そちらのブログで私が発言が出来る場を与えて下されば。サイコーです。
まだまだ言いたいことはあるのですが(何せ、こちらは長年我慢してきましたから)、また、こんな、大量にコメントしたら、こちらでは、ご迷惑に思われているかもしれませんし、またこのような古い記事ではオーディエンスもあまり集まらないでしょうし・・・、
私も、来週から忙しいので、今後は今迄みたいにチェックしませんが(する度にまた別の言いたいことが次々に浮かんでくるもので・・・)、まあ、1年以内にはお返事できると思うんで・・・。
よろしくお願いします。
度々の、超長文の乱筆、乱文、失礼しました。
合成関数について訂正に来ただけだったのにな…。