平昌オリンピックが盛り上がってきましたが、今年の一般入試もいよいよ本格化してきましたね。というわけで、今年の立命館大学の理系第1問を解説します。
《問題》
〔1〕正の整数$c$に対し、$x>0$ で定義された関数$$f_c(x)=\dfrac{\log x}{x^c}$$を考える。$f_c(x)$は $x={\fbox{ ア }}$ で最大値 ${\fbox{ イ }}$ をとり、$0<x \leqq {\fbox{ ア }}$ で増加し$x \geqq {\fbox{ ア }}$ で減少する。$\displaystyle \lim_{x \to +0}f_c(x)={\fbox{ ウ }}$ であり、また、$f_c(x)={\fbox{ エ }}f_{\frac{c}{2}}(x)$を用いると、$\displaystyle \lim_{x \to \infty}f_c(x)={\fbox{ オ }}$ となる。
〔2〕正の実数$s$に対し、$t>s$ かつ $s^t=t^s$ を満たす$t$が存在するための必要十分条件は、${\fbox{ カ }}<s<{\fbox{ キ }}$ である。
$a^b=b^a$ を満たす自然数$a$、$b$($a<b$)の組$(a,\ b)$は ${\fbox{ ク }}$ である。(注:自然対数の底$e$は $2<e<3$ であることを用いてよい。)
(立命館大学2018年理系 第1問)
《考え方》
本問は使い古された題材であり、〔2〕の結論部分は良く知られていることと思います。丁寧な誘導が設定されているので、かなり控えめな難度の出題です。
$f_c(x)$の導関数は$$\begin{align}f’_c(x) &=\dfrac{x^{c-1}-cx^{c-1}\log x}{x^{2c}} \\ &=\dfrac{1-c\log x}{x^{c+1}}\end{align}$$となり、$x=e^{\frac{1}{c}}$ で最大値$\dfrac{1}{ec}$をとります。また、$$\begin{align} f_{\frac{c}{2}}(x)&=\dfrac{\log x}{x^{\frac{c}{2}}} \\ &=\smash[t]{\sqrt{x^c}}\cdot \dfrac{\log x}{x^c} \\ &=\smash[t]{\sqrt{x^c}} \cdot f_c(x) \end{align}$$より、$f_c(x)=x^{-\frac{c}{2}} f_{\frac{c}{2}}(x) \ \ \ \cdots (*)$ となります。増減表より $f_c(x) \leqq \dfrac{1}{ec}$ ですから$(*)$式より$$f_c(x) \leqq \color{red}{x^{-\frac{c}{2}}} \cdot \dfrac{2}{ec}$$を得ます。$x \to \infty$ のとき $x^{-\frac{c}{2}} \to 0$ となるので、$x>1$ で $f_c(x)>0$ であることから、はさみうちの原理より、$$\displaystyle \lim_{x \to \infty}f_c(x)=\color{red}{0}$$となります。
$\displaystyle \lim_{x \to +0}f_c(x)=\color{red}{-\infty}$ と合わせると、増減表は以下のようになります。
| $x$ | ($0$) | ・・・ | $e^{\frac{1}{c}}$ | ・・・ | ($0$) |
| $f’_c(x)$ | $+$ | $0$ | $-$ | ||
| $f_c(x)$ | ($-\infty$) | ↗ | $\dfrac{1}{ec}$ | ↘ | ($0$) |
さて、本題は〔2〕の方ですが、先程も述べた通り本問は非常に有名な問題の一つで、$2^4=4^2$ しか自然数解が存在しないことは広く知られていることと思います。
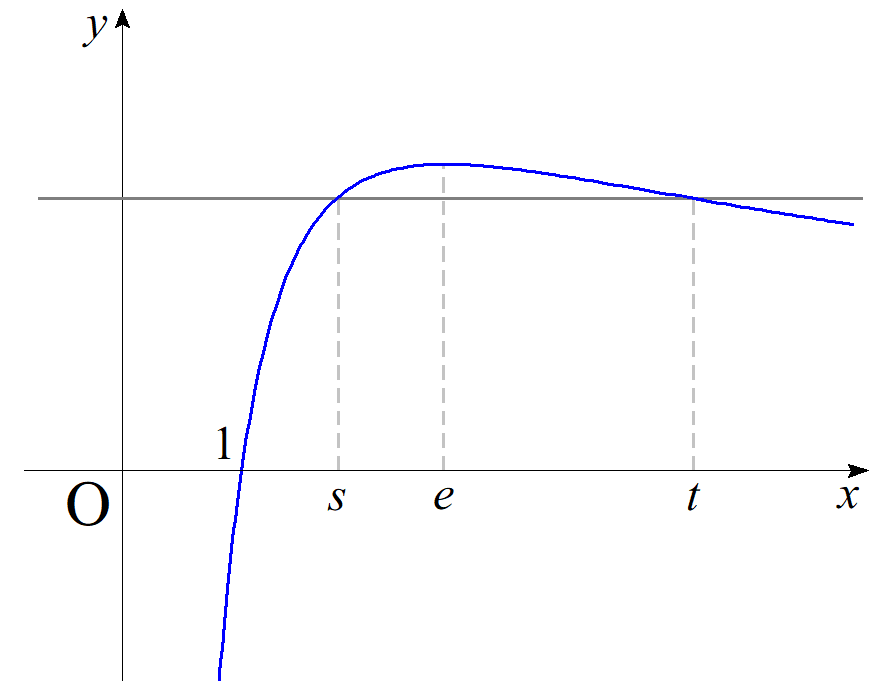
$s<t$ の条件の下で$$s^t=t^s$$を満たすとき、両辺に自然対数をとって整理すると$$\dfrac{\log s}{s}=\dfrac{\log t}{t}$$となります。これは〔1〕の$f_c(x)$について $c=1$ としたときに相当します。$y=f_c(x)$ の増減表より、$y=f_1(x)$ のグラフは以下のようになり、実数$s$に対してこのような実数$t$が存在するためには、$\color{red}{1}<s<\color{red}{e}$ が必要であることが分かります。
これと自然対数の底$e$が $2<e<3$ であることを利用すれば、等式$$a^b=b^a$$を満たす自然数$a$は $1<a \leqq 2$ を満たさなければならないので候補は$2$のみとなり、実際に $(a,\ b)=\color{red}{(2,\ 4)}$ が解として見つかります。
(コメント)
しっかりした誘導が付いているので、試験場では落とせない問題だったのではないでしょうか。本問のように関数$\dfrac{\log x}{x}$の増減を利用する問題は出題頻度が高いので、誘導が無くても解けるようにしておきたいですね。例えば
「$99^{100}$と$100^{99}$の大小を比較せよ」
といった問題にも対応できるように準備しておくべきでしょう。
因みに、等式 $a^b=b^a$ を満たすようなすべての有理数の組 $(a,\ b)$ は、自然数$n$を用いて $\left( \left( 1+\dfrac{1}{n}\right)^n ,\ \left( 1+\dfrac{1}{n}\right)^{n+1} \right)$ として与えられます。この事実の証明はやや面倒なので割愛しますが、本問がこの式において $n=1$ の場合に相当するということについて、一応言及しておきます。なお、この式により、等式 $a^b=b^a$ を満たすような有理数の組を小さい方からすべて求めることができます。$\left( 1+\dfrac{1}{n}\right)^n \to e$ となることから、「ふ~ん、そうなんだ」くらいには思って頂けるのでは。
なお、2015年の名古屋大学理系第1問に本問の類題があります。
【追記】
今回の問題とは全く関係ありませんが、「2018年冬の陣」を公開しました!今回で7作目の模試となりました。我ながらよくも飽きずにやっていると思ってしまいますね・・・。暇で暇で死にそうな方がいらっしゃれば、是非解いてみて下さい(笑)。
(※注:「2018年冬の陣」というのは年2回、管理人が道楽で作っている自作模試です)