特定の条件を満たすような図形の通過領域を求める問題は難関大で頻出です。今回は千葉大学の入試から通過領域に関するシンプルな良問を取り上げます。
放物線 $C:y=x^2$ 上の2点$\mathrm{A}$、$\mathrm{B}$は、直線$\mathrm{AB}$と$C$で囲まれる図形の面積が$\dfrac{1}{6}$になる、という条件を満たしながら$C$上を動くとする。このとき、直線$\mathrm{AB}$が通りうる点の範囲を求め、図示せよ。
(2003年千葉大学前期理系 第2問)
考え方
まずは2点$\mathrm{A}$、$\mathrm{B}$の$x$座標を$a$、$b$のように置き、問題文の条件を満たすような直線$\mathrm{AB}$の方程式を求めましょう。与えられた条件によりパラメータの一方が消去できます。領域を求める方法は順像法でも逆像法でも構いません。本問の場合は方程式が$a$の2次式を含むので、どちらかと言えば逆像法による解法が簡明でしょう。
解答例
2点$\mathrm{A}$、$\mathrm{B}$の$x$座標を$a$、$b$と置き、$a<b$ を仮定する。
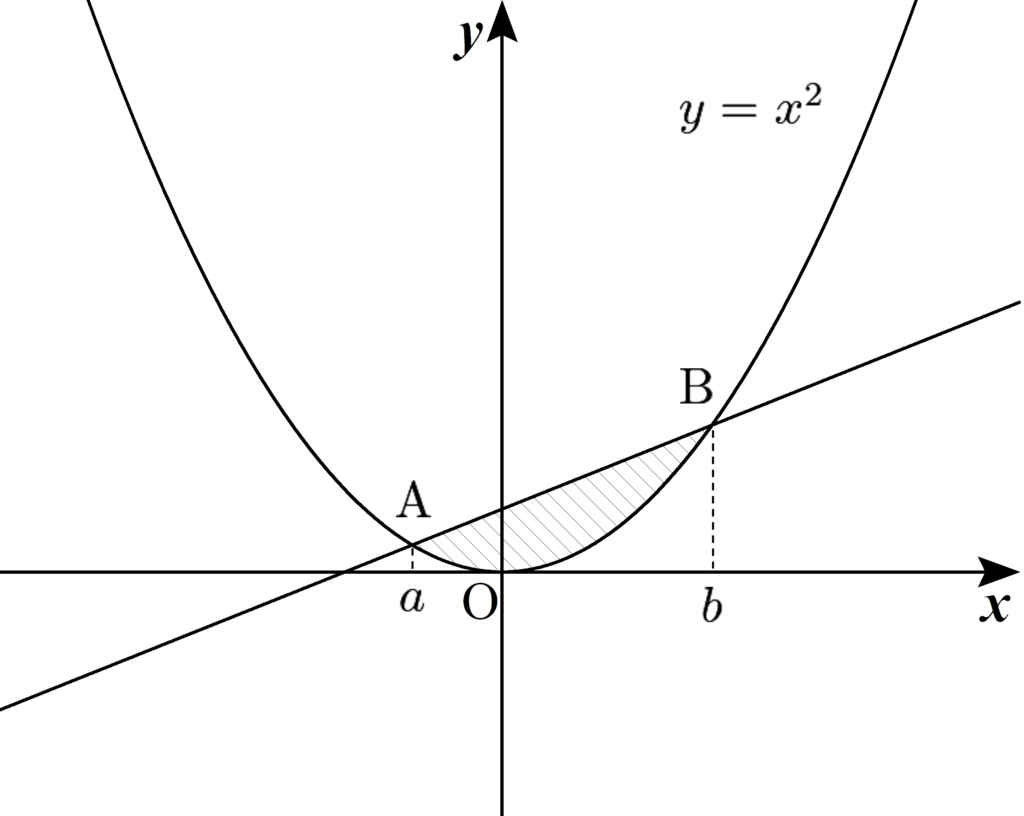
$\mathrm{A}(a,a^2)$、$\mathrm{B}(b,b^2)$より、直線$\mathrm{AB}$の方程式は$$y=\frac{b^{2}-a^{2}}{b-a}(x-a)+a^{2}$$ $$\therefore \quad y=(a+b) x-a b$$となるから、直線$\mathrm{AB}$と放物線$C$とで囲まれる部分の面積$S$は$$\small \begin{aligned}
S &=\displaystyle \int_{a}^{b}\left\{(a+b) x-a b-x^{2}\right\} \,d x \\
&=\displaystyle -\int_{a}^{b}(x-a)(x-b) \,d x \\
&=\dfrac{1}{6}(b-a)^{3}
\end{aligned}$$と表せる。問題文の仮定より $S=\dfrac{1}{6}$ となるから、$$\dfrac{1}{6}(b-a)^{3}=\dfrac{1}{6}$$ $$\therefore \quad b-a=1$$を得る。$b=a+1$ を直線$\mathrm{AB}$の方程式に代入すると$$y=(2 a+1) x-a^{2}-a \ \cdots ①$$となる。
$a$は全ての実数値をとりうるから、直線$\mathrm{AB}$が通過する領域は、式$①$を$a$の2次方程式と見たときに実数解$a$をもつような点$(x,y)$の集合に対応する。式$①$を$a$について整理すると$$a^{2}-(2 x-1) a-x+y=0$$となる。これが実数解$a$をもつためには判別式$D$が $D \geqq 0$ を満たせばよい。$$\begin{aligned}
D &=(2 x-1)^{2}-4(-x+y) \\
&=4 x^{2}-4 y+1
\end{aligned}$$より、点$(x,y)$が満たすべき条件は$$y \leqq x^{2}+\dfrac{1}{4} \quad \cdots (\text{答})$$と求められる。よって、直線$\mathrm{AB}$が通過する領域は下図の斜線部(境界線を含む)である。
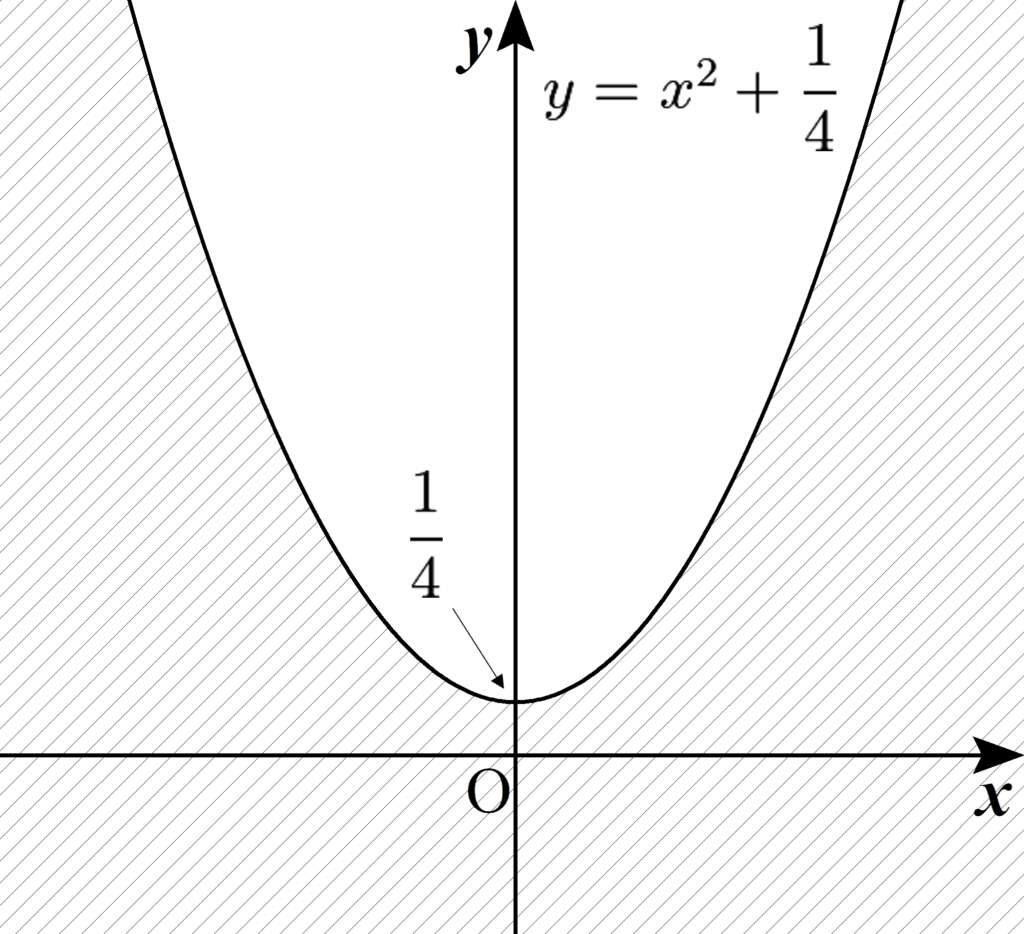

逆像法は強力な手法ですが、その理屈を正しく理解できていないと大怪我をしてしまうことがあります。やってることはといえば、以下のような数学的な「意味のすり替え」に過ぎません。
「点$\small (x,y)$がある図形(今回の場合は直線)の通過領域に属する」ということは、「点$\small (x,y)$を通るような直線 $\small y=(2 a+1) x-a^{2}-a$ が存在する」ということであり、これはつまり「方程式 $\small y=(2 a+1) x-a^{2}-a$ を満たすような実数$\small a$が存在する」ということを意味します。こうした数学的な意味の取り換えを進めていくことで、最終的に実数条件が登場するのです。
本問のような通過領域の問題を解答するときに、なぜ実数条件を考えなければならないのかを理解しないまま逆像法を使っている人は多い印象です。訳も分からずとにかく変数を実数条件に突っ込めば良いというのは大きな間違いです。いわゆる数学Ⅰ・Aの「解の配置」の問題をみっちり訓練しておくことは、こういう問題でミスをしないようにするためにも重要です。
なお、本問は順像法でも簡単に解けます。以下、$x$をある定数と見なします。式$①$について$$\small \begin{aligned}
y &=(2 a+1) x-a^{2}-a \\
&=-a^2+(2x+1)a+x \\
&=-\left(a-\dfrac{2x-1}{2}\right)^2+ x^{2}+\dfrac{1}{4} \ \cdots ②
\end{aligned}$$と平方完成できます。$a$は全実数の範囲を動くので、$②$の最小値は存在せず、$\small a=\dfrac{2x-1}{2}$ のとき最大値 $\small x^{2}+\dfrac{1}{4}$ をとります。これより、ある$x$に対して$y$の取り得る範囲は $\small y \leqq x^{2}+\dfrac{1}{4}$ となり、この結果はすべての実数$x$について成立するので、これが求めるべき通過領域に一致します。これが順像法による解き方です。
通過領域問題に苦手意識を持っている人は多いので、攻略するのが早ければ早いほど差が付きます。通過領域の問題の解き方や考え方については「通過領域問題の攻略法」の記事に詳しくまとめてあります。順像法と逆像法の使いどころの解説をシリーズ化してあるので是非参考にして下さい!