2次曲線を方程式の係数で分類する

本稿では方程式の一般形から2次曲線の種類を判別する方法を解説します！

コンテンツ

・2次曲線とは

・2次曲線の種類を調べる公式

・係数で分類する

2次曲線とは

実数の変数$x$、$y$を用いて$$Ax^2+Bxy+Cy^2+Dx+Ey+F＝0$$という形の方程式で表される曲線は「2次曲線」と呼ばれます。ここで$A$～$F$は実数の定数で、これらの値によって曲線の形が決まります。

例えば、方程式$$4x^2-4xy+3y^2+x-3y-5＝0$$によって陰関数表示される曲線は次のような楕円になります。

また、方程式$$x^2+3xy-2y^2+x-2y+9＝0$$によって陰関数表示される曲線は次のような双曲線になります。

（メモ）

※これらのグラフは「desmos」というオンラインアプリを用いて表示しており、図の右下のアイコンがウェブサイトへのリンクになっています。リンク先では自由にパラメータをいじって曲線の形を変えることができます。多項式だけでなく様々な関数がサポートされているので、是非遊んでみることをお勧めします！

しかし一般の2次曲線の方程式だけを見ても、どんな2次曲線を表しているのかはよく分かりません。そこで公式の出番です。

2次曲線の種類を調べる公式

2次曲線$$Ax^2+Bxy+Cy^2+Dx+Ey+F＝0$$の係数から曲線の種類を決定するための「判別式」（discriminant; $\varDelta$）が知られています。$$\color{red}{\varDelta=4AC-B^2}$$判別式$\varDelta$の正負と係数$A$～$F$の条件によって、2次曲線の種類を以下のように判別できます。

- $\varDelta=0$ かつ $2AE-BD \ne 0$ のとき、2次曲線は「放物線」となる。
  ただし $B=0$ かつ $A$と$C$のいずれか一つのみが$0$のときは $2AE-BD=0$ でも「放物線」となる。
- $\varDelta=0$ かつ $2AE-BD=0$ のとき、2次曲線は「平行な2直線」もしくは「1直線」となる。
  ただし $A=B=C=0$ のときは $2AE-BD=0$ でも「平行な2直線」もしくは「1直線」となる。
- $\varDelta>0$ のとき、2次曲線は「楕円」となる。
  ただし係数の値によっては「曲線が存在しない」（実数解無し）もしくは「1つの点」の場合もある。
- $\varDelta<0$ のとき、2次曲線は「双曲線」となる。
  ただし係数の値によっては「交わる2直線」の場合もある。

これらの「公式」は、大雑把には以下のように正当化できます。

まず前提として、曲線の方程式に直線の方程式を加えても軸の向きや漸近線の傾きが変わるだけで、曲線の種類には影響しません。つまり、曲線の種類を調べるためには方程式の $Ax^2+Bxy+Cy^2$ の部分だけ見れば良いことになります。

※これは、平行移動や拡大縮小など座標軸の変換を考えれば、すべての2次曲線が $ax^2+bxy+cy^2=k$ という形の方程式で表現できることに対応します。

そこで $ax^2+bxy+cy^2=k$ を2次曲線の代表として考察してみます。式の対称性を考えて $a>0$ の場合を考えれば良いでしょう。このとき左辺は$$\begin{aligned}
& \quad \ a x^{2}+b x y+c y^{2} \\
&= a\left(x^{2}+\frac{b}{a} y x+\frac{b^{2}}{4 a^{2}} y^{2}\right)-\frac{b^{2}}{4 a} y^{2}+c y^{2} \\
&= a\left(x+\frac{b}{2 a} y\right)^{2}+\left(c-\frac{b^{2}}{4 a}\right) y^{2}
\end{aligned}$$と式変形できます。ここで $X \equiv x+\dfrac{b}{2 a} y$、$Y \equiv y$ と置けば、$$ \color{red}{aX^{2}+\left(\frac{4ac-b^{2}}{4 a}\right) Y^{2}=k}$$と標準形に直すことができます。いま$a$は正なので2次曲線の種類は$Y^{2}$の係数の正負によって決まります。

つまり $4ac-b^{2}$ の符号によって、この2次曲線が楕円なのか、双曲線なのか、放物線なのかが決まるというわけです。これが判別式$\varDelta$の正体です。

※なお、$X \equiv x+\dfrac{b}{2 a} y$ という置き換えはベクトル$\left(1,-\dfrac{2a}{b}\right)$方向に$X$軸を取り直すことに相当しています。この数学的操作は「基底の変換」などと呼ばれています。

※1次の項が存在する場合、つまり与方程式が$$ax^2+bxy+cy^2+dx+ey=k$$で表される場合は次のように考えます。$X \equiv x+\dfrac{b}{2 a} y$、$Y \equiv y$ と上記同様の変形を施した後、さらに $x \equiv X-\dfrac{b}{2 a} Y$ として$x$を消去すると$$a\left(X+\dfrac{d}{2a}\right)^2+\dfrac{2ae-bd}{2a}Y=k+\dfrac{d^2}{4a}$$を得るので、これが放物線となるためには$Y$の1次の項の係数が$0$でなければよく、$2ae-bd \ne 0$ の条件を得ます。

係数で分類する

それでは実際に判別式$\varDelta$を使って2次曲線を分類してみましょう。

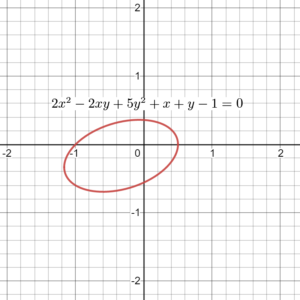
① $\small 2x^{2}-2xy+5y^{2}+x+y-1=0$

$$\begin{align} \varDelta &=4 \cdot 2 \cdot 5- (-2)^2 \\ &=36 >0 \end{align}$$より、これは楕円の方程式です。グラフは以下のようになります。

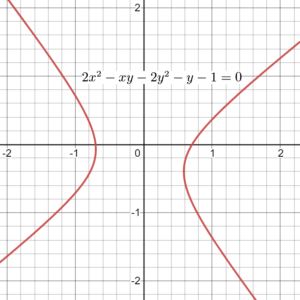
② $\small 2x^{2}-xy-2y^{2}-y-1=0$

$$\begin{align} \varDelta &=4 \cdot 2 \cdot (-2)- (-1)^2 \\ &=-15<0 \end{align}$$より、これは双曲線の方程式です。グラフは以下のようになります。

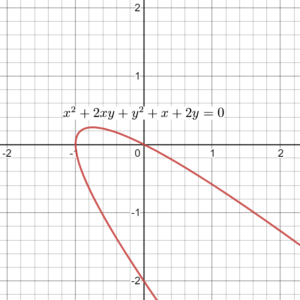
③ $\small x^{2}+2xy+y^{2}+x+2y=0$

$$\varDelta=4 \cdot 1 \cdot 1- 2^2=0 $$より、これは放物線の方程式です。グラフは以下のようになります。

④ $\small x^{2}+2xy+y^{2}+x+y=0$

これは③の式の$2y$を$y$に変えた方程式です。$$\varDelta=4 \cdot 1 \cdot 1- 2^2=0 $$となるので放物線…と判断しそうになりますが、$2AE-BD=0$ が成り立つのでこれは2本の直線を表す方程式です。グラフは以下のようになります。

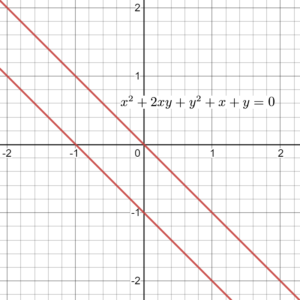
特にこの方程式については$$(x+y)(x+y+1)=0$$と因数分解できるので、$$\left\{\begin{array}{l}x+y=0 \\ x+y+1=0\end{array}\right.$$という連立方程式に書き改められます。このことから2本の直線を表していることが理解できます。

今回紹介した判別式で分類する方法は、式の形や符号を忘れてしまっても平方完成すれば自力で導出可能です。方程式の係数から2次曲線の種類を系統的に分類する方法があるのだということは知っておきましょう。使いどころは多くありませんが便利なので覚えておきたい知識です。

前回の投稿でも述べましたが、2次曲線に親しむためには自分でグラフを色々と描いてみるのが一番良いです。最近では陽関数も陰関数もラクラク描画をこなす便利なオンラインアプリが無料で利用できます。冒頭で紹介したオンラインアプリ「desmos」もその一つです。せっかくインターネット全盛の時代に生きているのですから、使わないのは損というもの。特に受験生の方や、受験生を指導する立場の方に積極的に使って欲しいと思います。

(2023/05/22：場合分けの条件の誤りを修正、補足説明を追加）