今回は数学ⅡＢでいきなりラジアンの定義が出題されました。面食らった受験生が結構いたのではないでしょうか･･･？また、第２問の微積分でも不定積分の定義の出題がありました。
センター試験の本命は勿論数学です(笑)。今年の問題を一見して、言うまでもなく目に付いたのが数ⅡＢの第１問。初っ端からこの設問では、不意を突かれた受験生もかなり多かったことと思います。
（図１．2018年センター試験 数学ⅡＢ第１問 抜粋）
おや、そういえば2015年にもこんな問題あったような･･･と思って探してみると、やはり有りましたね･･･。似た問題が。
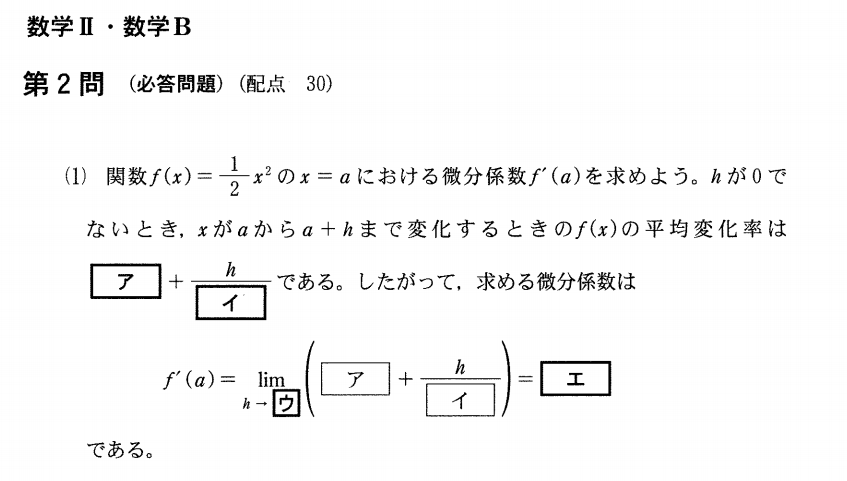（図２．2015年センター試験 数学ⅡＢ第２問 抜粋）
数学においては単元の基本となる定義を押さえることが最も重要です。高校数学の構成や展開には数学的に様々な欠陥があるのは周知の事実でしょうが、それでも数学を勉強していく上で蔑ろにできるものではありません。
余談ではありますが、２次試験でも定義を確認させる問題は多数出題されています。例えば、1999年には東大数学の三角関数の定義を述べさせる問題が出題され、1999年の京大後期には積分による平均値の定理の証明が出題されていますし、2003年の東大では円周率の評価の問題、佐賀大では2008年に正弦定理の証明、2011年には三角関数の合成の一般化が出題されており、2013年には阪大文系で点と直線の距離の公式の導出、阪大理系では $\displaystyle \lim_{x \to 0} \dfrac{\sin x}{x}=1$ を証明させた上で、$\sin x$ の導関数が $\cos x$ であることの証明が出題されています。また、阪大では2014年の挑戦枠で原始関数と不定積分の違いに関する出題もありました。そして2015年には上述の通り、センター数ⅡＢで微分係数が出題されましたね。この他にも定義や定理に関する出題が多数出題されています。
そんなわけで、公式や定理の証明は勿論のこと、定義に関する出題が最近の入試問題のトレンドなのです。そこで今年のセンターではラジアンの定義ですか･･･。なかなか乙な出題とも言える一方で、そこはかとなくネタ切れ感(笑)も漂ってくる、そんなセンター数ⅡBでした。
● ● ● ● ●
まずこれを見たとき、
「そもそも、ラジアンというのは数ⅡBの範囲だったっけ？」
という疑問が浮かびました。そこで調べてみるとサインやコサインといった三角法は数学ⅠＡの範囲ですが、弧度法を初めて学ぶのは数学ⅡＢということでした（勉強不足でスミマセン）。そう言われてみると、サインやコサインは数ⅡＢで「三角関数」として改めて扱うことになるのでしたね･･･。
さて、件のラジアンですが、そもそも「ラジアン」というのは単位であることに注意しましょう。つまり「メートル」や「リットル」と同じように扱われるものなのです。ただ、ここで「単位」と断言すると誤解を招いてしまうかもしれませんので一応お断りしておきますと、ラジアンはあくまで「度（°）」と同じく「無次元量の」単位です。物理的な単位ではないですので、その点だけ留意して下さい。
さて、そこでラジアンを使いますと、
$180^{\circ}=\pi$ラジアン
となります。数学では普通、単位の「ラジアン」を省略してしまうので、次のようになります。
$180^{\circ}=\pi$
これなら皆さんにも「な～んだ、当たり前じゃん」と納得してもらえるのでは。
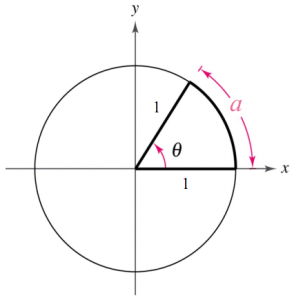（図３．単位円における弧度法）
要は、単位円（＝半径が$1$の円）における「弧の長さ$a$」と「中心角$\theta$」を対応させたものをラジアンと呼ぶのです。図３においては
$a=\theta$（ラジアン）
が成立します。これは何も不思議なことではなく、皆さん普通にやっていることです。例えば、$90^{\circ}$の角度に対応する単位円の弧の長さは$\dfrac{\pi}{2}$ですよね。これを
$90^{\circ}=\dfrac{\pi}{2}$（ラジアン）
と書いている、というだけのお話です。角度を弧の長さに対応させるだけなので、単位円を$r$倍すれば角度はそのままで弧の長さだけが$r$倍されます。単なる相似拡大なので、長さは$r$倍されます。
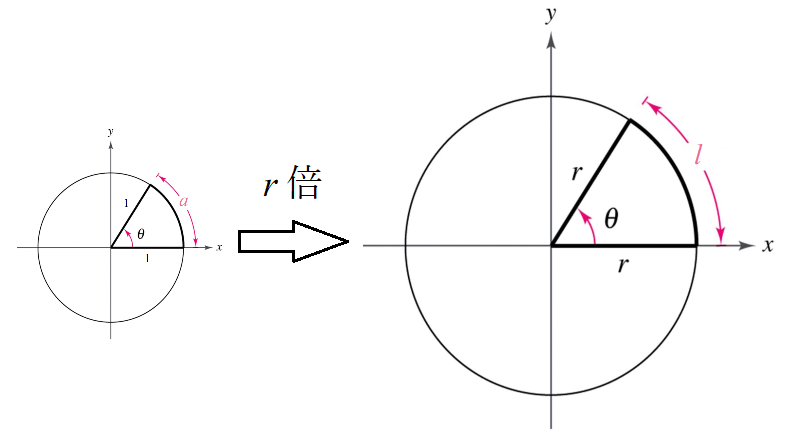（図４．単位円を$r$倍した円における弧度法）
つまり単位円では$a$だった弧長が、円を$r$倍すると円の半径は当然$r$となり、弧長$l$は$ra$、つまり
$l=ra=r \theta$
と表せるのです。これが弧度法の便利なところで、もし弧度法ではなく角度でこれをやると、円周率$\pi$が無理数であるためにとても不便になります。例えば、単位円における半円の場合、
$3.1415…=1 \times 180^{\circ}$
となってしまいます。弧度法だと$\pi$がそのまま使えるから便利なのです。（※理解のある方なら分かって頂けると思いますが、弧度法と区別するために敢えて小数表示しています）
上記の説明を読むのが煩わしければ以下に示すgif画像で納得して下さい(笑)。
（図５．Circle radians）
という訳なので、正答は
「２」
と結論できます。難関大を目指す受験生であれば瞬殺して欲しいところですが、実際のところはどうなっているのやら･･･？
● ● ● ● ●
今回のラジアンの一件もそうですが、全体を通して理系科目の設問は、少し前までの傾向だったゴリゴリの計算主体というよりも、定性的な内容に関する問いが増えた印象を受けました。これも３年後に控えた「大学入学共通テスト（新テスト）」への布石なのでしょうか･･･。
また、数学ⅡＢでは第２問の微積分でも定義に関する出題がありました。不定積分と定積分がごっちゃになっていると選択肢で間違えてしまいます。
（図６．2018年センター試験 数学ⅡＢ第２問 抜粋）
定義をおさらいします。
・不定積分：$F'(x)=f(x) \iff \displaystyle \int f(x)dx=F(x)+C$
・定積分：$\displaystyle \int^{b}_{a} f(x)dx=\left[F(x)\right]^{b}_{a}=F(b)-F(a)$
これが定義です。知らなかったとしても、皆さん多分どこかで習っているはずですよ(笑)。
$x$の関数$F(x)$と$f(x)$があって、$F'(x)=f(x)$ のとき、$F(x)$を$f(x)$の原始関数と定めるのでした。また、$f(x)$の原始関数の１つを$F(x)$とするとき、$F(x)+C$ を $\displaystyle \int f(x)dx$ と書いて、これを$f(x)$の不定積分と呼びます（$C$は積分定数）。
一方、定積分には文字定数$C$が不要で、$f(x)$の原始関数の１つを$F(x)$とするとき、$F(b)-F(a)$ を
「$f(x)$の下端 $x=a$ から上端 $x=b$ までの定積分」
と呼び、$\displaystyle \int^{b}_{a} f(x)dx$、或いは$\left[F(x)\right]^{b}_{a}$と表すのでしたね。また、この問題では次の微分と積分の関係式を利用します。ここで$a$は定数です。
$$\begin{align} \dfrac{d}{dx}\displaystyle \int^{x}_{a} f(t)dt &=\dfrac{d}{dx}\left[F(x)\right]^{x}_{a} \\ &= \dfrac{d}{dx}\{F(x)-F(a)\} \\ &=F'(x) \\ &=f(x) \end{align}$$
これにより、不定積分及び境界値から元の関数を求めることができるのでした。したがって正答は
$F'(x)=\color{orange}{f(x)}$
（選択肢 ツ：「7」）
$W=\color{orange}{-F(t)+F(1)}$
（選択肢 テ：「4」）
$f(t)=\color{orange}{-6t^2+2}$
（選択肢 ト～ヌ：「$-$・6・2・2」）
となります。解答の際は $f(x)<0$ という条件に注意しましょう。「定積分」ではなく「面積」が主題なので符号に十分注意する必要があります。また、無いとは思いますが、$F(1)$が定数であることを忘れないように･･･。結論としては$$W'(t)=-f(t)$$となります（ここでは面積$W$を$W(t)$として$t$の関数とみなしています）。問題文の条件より $W(t)=2t^3-2t$ となりますから $f(t)=-6t^2+2$ と求められます。
● ● ● ● ●
正直、今回の問題量だと以前当サイトで紹介した「$\dfrac{1}{3}$公式」を設問〔１〕で使っても大してお得感はないかもしれませんね(笑)。数ⅠＡが少し難しかったかもしれませんが、問題数も減って全体的に易化の傾向があります。センター側も攻略されまいと躍起なのでしょうか。
結局、２日間通して見ると、１日目のテストの方が遊び心がありましたね(笑)。
ともあれ、ひとまずはセンター試験お疲れ様でした。今日くらいはゆっくり休んでも良いのでは。但し、センター試験は通過点に過ぎません。２次試験に向けて、引き続きしっかり対策していって欲しいと思います！