2022年1月18日2022年7月31日投稿者: pencil

2022年共通テスト数学ⅠＡの解説と雑感

今年も受験シーズンがやってきました。受験生の皆さん、まずは共通テストお疲れ様でした。持てる力を存分に発揮できたことと思います。本稿では試験直後から難化が話題となった2022年共通テスト数学ⅠＡについて、管理人が問題を解いた雑感を書き連ねていきます。

（2022/01/26追記；2022年共通テスト数学ⅡＢについてはこちら）

全体の概観

「センター試験」から「共通テスト」に移行して全体的に図表が多くなった印象を受けますが、出題範囲や問題の大枠は例年のものを踏襲しているようです。この時点ではそれほど凶悪な印象は受けませんでした。しかし解き進めてみると、まあ大変ですね…。時間の取られる問題が多く、タイムロスからの復帰が難しいセットだったと感じました。これを受験された方々は本当にお疲れ様でした…。

以下、長々と個人的な雑感を書いていきます。乱文ですがご容赦下さい。問題文は掲載していませんので、適宜お手元にご用意を。

数学ⅠＡ第１問

〔１〕は単純な計算問題でした。登場する文字が多いですが頭を使うような問題ではありません。等式 $(x+y)=x^2+2xy+y^2$ から積$xy$を求める手順も定石通りです。注意する点は符号ミスくらいでしょうか。落ち着いて取りたいですね。

〔２〕は少し目新しい感じがしました。ただ、地図の読み取りとはいっても、実際には単なる比の計算に過ぎません。

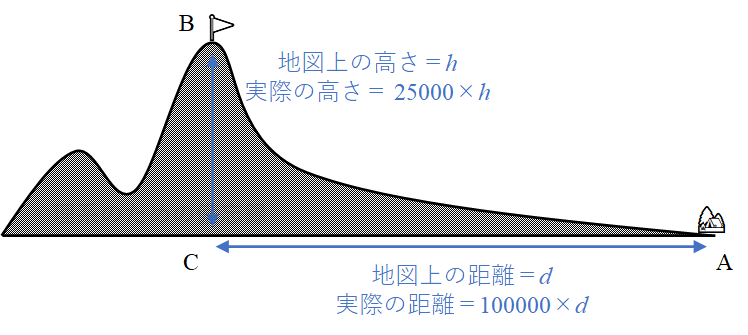
地図上での仰角 $\angle \mathrm{BAC}=16^{\circ}$ の正接（タンジェント）は三角比の表から $\tan 16^{\circ} \approx 0.2867$ と読み取れます。地図上での山の高さを$h$、山頂までの距離を$d$と置くと、正接の定義から $\dfrac{h}{d}=\tan 16^{\circ} \approx 0.2867$ となっています。
そこで、実際の仰角を$\theta$と置くと、$$\begin{aligned} \tan \theta &=\dfrac{25000 \times h}{100000 \times d} \\ &=\dfrac{1}{4} \times \frac{h}{d} \\ &\approx \dfrac{1}{4} \times 0.2867 \\ &\fallingdotseq \color{red}{0.072} \end{aligned}$$と求められます。この値について表を参照すると$$\tan 4^{\circ}<\tan \theta<\tan 5^{\circ}$$を満たすから$$4^{\circ}<\theta<5^{\circ}$$と結論できます。見慣れない設定かもしれませんが、別に難しくはありません。

余談ですが、本問は昨年話題となった「イージスアショア」の配備地選定の調査報告書（外部リンク）を踏まえた時事ネタである可能性が指摘されています。角度の数値もかなり似通っており、仰角が本来より大きくなっていたというシチュエーションも本件にそっくりです(笑)。「図形と計量」は国防の観点でも非常に大切です…。

あまり居ないとは思いますが、四捨五入しろなんて書いてない！とお怒りの受験生の方は問題冊子の裏表紙をよく読んでから受験するようにしましょう。

〔３〕は平面図形と二次関数の融合問題でした。（１）は正弦定理を使えばすぐに解決します。問題は（２）でしょう。$2 \mathrm{AB}+\mathrm{AC}=14$ という条件に囚われすぎると本質的な条件がすっぽ抜けてしまう恐れがあります。

問題文で「外接円の半径が$3$」と書いてあるので、内接する三角形の辺はどんなに長くても直径以下、すなわち$6$以下に制限されます。特に条件で制約されていなければ $0 \leqq \mathrm{AB} \leqq 6$ となるはずですが、仮に $\mathrm{AB}=0$ としてみると条件式より $\mathrm{AC}=14$ になって「おや？」となります。

そこで$\mathrm{AC}$の方を考えます。こちらも長さの最大値は$6$のはずなので $\mathrm{AC}=6$ を条件式に入れると $\mathrm{AB}=4$ となります。これが長さ$\mathrm{AB}$の最小値です。

$\mathrm{AB}=6$ のときは $\mathrm{AC}=2$ となるので、これも良さそうです。以上から$\mathrm{AB}$の長さのとり得る値の範囲は $4 \leqq \mathrm{AB} \leqq 6$ と決まります。

$\mathrm{A D}$については（１）と同様に正弦定理を利用すれば良いでしょう。$$\begin{aligned} \overline{\mathrm{A D}} &=\overline{\mathrm{A B}} \times \frac{\overline{\mathrm{A C}}}{2 R} \\ &=\overline{\mathrm{A B}} \times \frac{1}{6}(14-2 \overline{\mathrm{A B}}) \\ &=\color{red}{\frac{-1}{3} \overline{\mathrm{A B}}^{2}+\frac{7}{3} \overline{\mathrm{A B}}} \end{aligned}$$これは$\overline{\mathrm{A B}}$軸の切片が $\overline{\mathrm{A B}}=0,\, 7$ の上に凸な2次関数なので、中央の $\overline{\mathrm{A B}}=\dfrac{7}{2}$ で最大になりそうな気になります。しかし計算しても解答欄に合いません。それもそのはずで、$\dfrac{7}{2}$ は長さ$\mathrm{AB}$の範囲外にあるため、最大値を与える$\overline{\mathrm{A B}}$は$4$となります（結果は $\overline{\mathrm{A D}}=4$）。

この〔３〕は時間喰い虫だったかもしれません。

関係式を一般化して $2\mathrm{AB}+\mathrm{AC}=p$ とした場合、$0<p<18$ の範囲では$\mathrm{AD}$の最大値が定義できます。一方で最小値に関しては $12<p<18$ の範囲であれば存在し、$p \leqq 12$ のときは2次式から単純に計算すると $\mathrm{AD}=0$ と三角形の成立条件を満たさないので存在しません。

数学ⅠＡ第２問〔１〕

何やら会話が始まっています。解の個数が話題のようです。

$$\begin{aligned}
&x^{2}+p x+q=0 & \cdots ①\\
&x^{2}+q x+p=0 & \cdots ②
\end{aligned}$$

（１）の前半は問題無いでしょう。方程式①が重解を持つので $n=3$ です。後半は少し注意が要ります。方程式①の解は $x=1,\,-2$ で、方程式②の解は $x=1$ となるので解の個数は $n=2$ です。重解を持っていなくても実数解が被ると$n$は減ります。

$n$が減少する状況として２つの場合があることをここで小問にしている辺り、何か示唆的です。

（２）で手こずった受験生は多かったかもしれません。会話文にしたがって連立方程式$$\left\{\begin{array}{l}{\alpha}^{2}-6 {\alpha}+q=0 \\ {\alpha}^{2}+q {\alpha}-6=0\end{array}\right.$$を考えて${\alpha}^2$を消去すると、$$(q+6)(\alpha-1)=0$$という式を得ます。$q=-6$ とすると方程式①と②は全く同じものになるので高々2個の実数解しか持たず、$n=3$ にはなりません。一方、$\alpha=1$ とすると方程式①より $q=5$ を得ます。このとき方程式①と②はそれぞれ$$\left\{\begin{array}{l}(x-5)(x-1)=0 \\ (x+6)(x-1)=0\end{array}\right.$$と因数分解できるので、実数解は $x=-6,\ 1,\ 5$ の3つになり、条件に適しています。

（１）で確認したように、$n=3$ となるのは「重解を持つ」か「解が重複する」のいずれかの場合です。そこで、もう一つの$q$は「重解を持つ」場合に得られるのではないか、と気が付くはず。そうすると、重解を持てそうなのは定数項が負でない方程式①のみで、$q=9$ とすると $n=3$ になることが分かります。（方程式②の解は $x=\frac{-9 \pm \sqrt{105}}{2}$ となり、実際に重複していません）

（３）はグラフの動きに関する問題でした。挿絵で登場人物がウレタンマスクをしていたりタブレット端末を使っていたりするのが時代を感じさせます。

$$\begin{aligned}
&x^{2}-6 x+q=0 & \cdots ③\\
&x^{2}+q x-6=0 & \cdots ④
\end{aligned}$$

係数にパラメータが含まれる曲線のグラフがどんな風に動くのかなんて、今まで考えたことも無かったという人は多いのでは？ただ、何が定数で何が変数なのかを理解していれば、おおよその見当は付くはずです。

例えば、③のグラフは1次の項の係数が定数なので、頂点の$x$座標は一定です。つまり上下方向にしかグラフは動きません。④のグラフは0次の項が定数なので$y$切片は変わらないままで$x$軸負方向に広がっていくイメージです。平方完成しても良いですが、しなくても解答可能です。

花子さんと太郎さんだけグラフ表示ソフトを使うなんてズルい！…ということで $p=-6$ で固定したときのグラフが動く様子を皆さんも体感してみてください。紫色のスライドで$q$の値を変えられます。両端でちゃんと $n=3$ になっていますよね。動きも確認してください。

（４）は前問の結果を集合に絡めた問題でした。部分集合$A$と$B$には重複する要素が無いので、

- $x \in A$は、$x \in B$ であるための「必要条件でも十分条件でもない」
- $x \in B$ は $x \in \bar{A}$ であるための「十分条件であるが必要条件ではない」

が解答となります。

数学ⅠＡ第２問〔２〕

今年のデータの分析はプロットされたデータ点を数える必要があり、「視力検査」と揶揄されるのも頷ける出題でした…(笑)。

まずは（１）から。何の変哲もない四分位数に関する問題ですが、最後の解答欄「ス」は少し注意が必要かもしれません。ヒストグラムからデータ点の属する階級は分かりますが、四分位範囲まではわからないことに注意してください。なぜなら、第1四分位数と第3四分位数の大小によって四分位範囲が逆転する場合もあるからです。解いているときに、この設問は引っ掛けのつもりなのかな、という気がしました。実際の正答率が気になります。

巷で「視力検査」と悪評の立っている問題が（２）です。参考までに、問題文中で与えられた箱ひげ図を重ねたプロットを掲載しておきます。（画質はボソボソですが…）

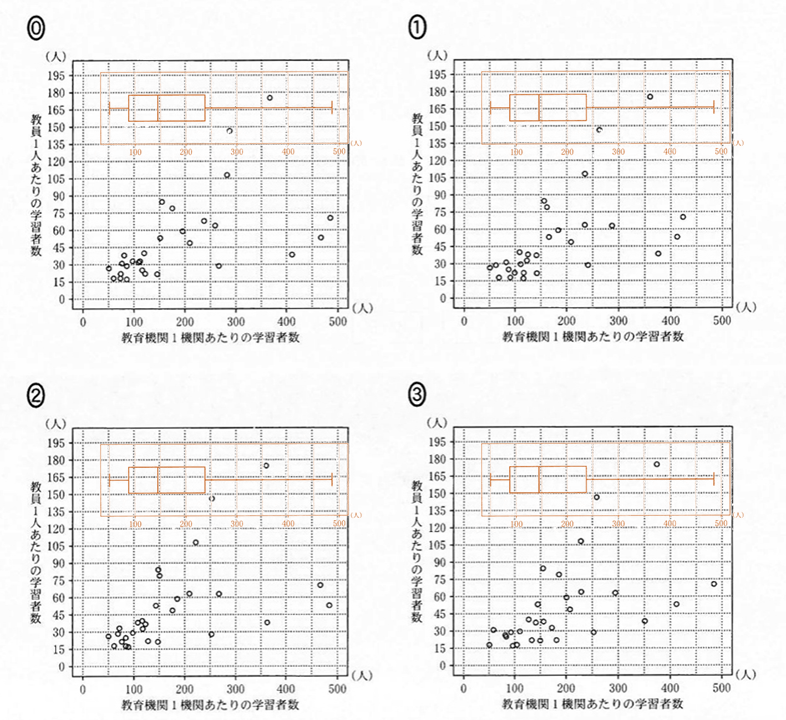
仕方ないのでマジメにデータ点を数えましょう。共通テストでは何か上手い方法がないかと思索している時間がそもそも勿体ない気がします。

⓪は上ヒゲの中にデータ点が8個以上含まれることから除外できます。

また、横軸の最大値が500に近いのに対して、①のプロットでは横軸が最大となる点でも420程度なので、①も除外できます。

③については、中央値～第3四分位数までの範囲にデータ点が9個存在することから除外できます。

以上から消去法によって②が正しいプロットであることが分かります。マーク式の試験では論証が不要なので手早く片付けたいところ。

（３）は相関係数の求値問題でした。$s_{x y}$を$x$と$y$の共分散、$s_{x}$および$s_{y}$をそれぞれ$x$および$y$の標準偏差とすると、相関係数は$$r=\dfrac{s_{xy}}{s_x s_y}$$で与えられます。これは公式を覚えていれば難なく $0.62574…$ と答えられるはずです（解答の際には四捨五入して$0.63$でマークする）。

それから、見聞きした話によると、表1に示された標準偏差の値を先に四捨五入して計算を簡単にしようとした受験生がいたようです。以下に表1を掲載します。$$\begin{aligned}
&\begin{array}{|c|c|c|c|c|}
\hline \begin{array}{c}
S \text{の} \\
\text{平均値}
\end{array} & \begin{array}{c}
T \text{の} \\
\text{平均値}
\end{array} & \begin{array}{c}
S \text{の} \\
\text{標準偏差}
\end{array} & \begin{array}{c}
T \text{の} \\
\text{標準偏差}
\end{array} & \begin{array}{c}
S \text{と} T \text{の} \\
\text{共分散}
\end{array} \\
\hline 81.8 & 72.9 & 39.3 & 29.9 & 735.3 \\
\hline
\end{array}
\end{aligned}$$確かに、$T$の標準偏差が$29.9$とあるので、これを$30.0$に丸めて計算を簡単にしても良さそうですが、実はこの操作は結果に影響してしまうのです。

$T$の標準偏差を$30.0$に丸めた場合は $0.62366…$ となり、四捨五入したときに$0.01$だけズレてしまいます。この設問の配点は3点と大きいので、$\pm 0.01$ 程度の誤差は部分点扱いにしても良いのでは…と思いますが、どうでしょうか？

（４）はオマケ問題のつもりで出題したのでしょうが、悪問寄りの出題です。

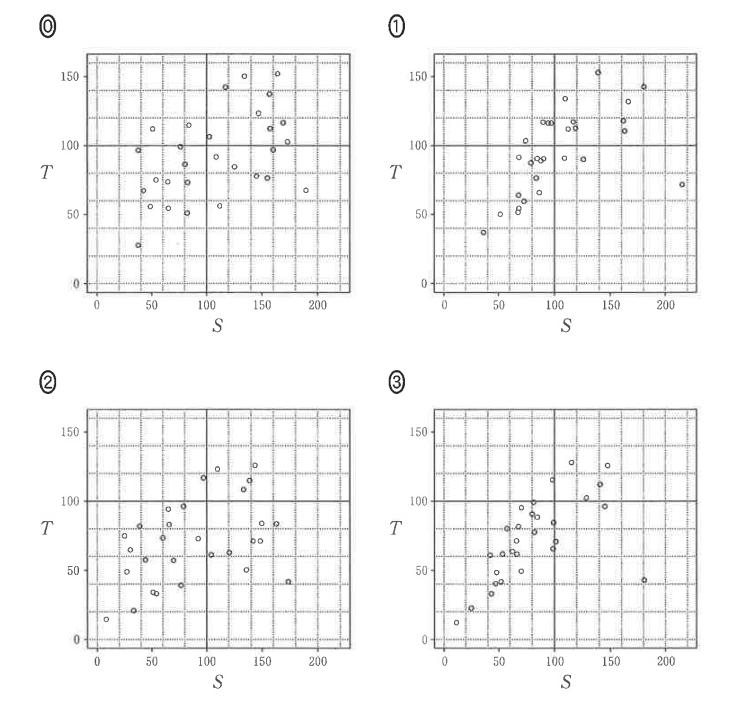
$T$の平均値が$72.9$なので、データ点が上側に偏っている⓪と①は除外できます。残るは②と③ですが、相関係数が$0.63$に近そうな(？)③のプロットを選びます。相関係数以外に標準偏差の値も根拠になるので、問題文の文言に過度に惑わされるとミスしそうです。

参考までに、相関係数と散布図のデータ点の分布の関係は大体以下のようになっています。（図の出典はWikipedia：相関係数）

この図の最上段を見て下さい。②のプロットはどちらかというと相関係数0の散布図に近いと言えます。作問者は恐らく正確な手計算を要求していないはずなので、「表1と(3)で求めた相関係数を参考にすると」との文言の通り、相関係数の値から大雑把に選ぶ趣旨の出題だったのだと思います。回答に際してフィーリングに頼らざるを得ないような問題は試験としてどうなの？という感じはします…。

一方で、表1には標準偏差も載っているので、ここから点の分布を割り出して正誤判断することも可能です。つまり、平均$\mu$と標準偏差$\sigma$について、$\mu \pm \sigma$ の範囲に含まれる点が多い③を選ぶということです。恐らく標準偏差も絡めて結論を導く解法が模範解答として各予備校から発表されるものと思います。難問です。

数学ⅠＡ第３問

「交換の結果,1人でも自分の持参したプレゼントを受け取った場合は,交換をやり直す」という部分が――現実のプレゼント交換としては真っ当なのですが――数学の問題としてはちょっとやりにくそうだなという第一印象を受けました。本問のテーマは「完全順列」です。この単語は聞いたことのある人もいるのではないでしょうか。

（ⅰ）2人で交換会を開く場合はプレゼントの配られ方が$2!$通りで、プレゼント交換が終了するのは相手のプレゼントを受け取った場合のみです。したがって、1回目の交換で交換会が終了するようなプレゼントの受け取り方は$1$通り。1回目の交換で交換会が終了する確率は$\color{red}{\dfrac{1}{2}}$です。

（ⅱ）3人で交換会を開く場合はプレゼントの配られ方が$3!$通りとなります。ここで、$A$、$B$、$C$の3人が持ち寄ったプレゼントを$a$、$b$、$c$として、プレゼントの受け取り方を$(a,b,c)$のように表記することにします。つまり、$(a,b,c)$は$A$、$B$、$C$の3人が全員自分のプレゼントを受け取った場合を表し、$(c,a,b)$は$A$が$c$、$B$が$a$、$C$が$b$をそれぞれ受け取った場合を表します。

プレゼント交換が終了するのは$(b,c,a)$か$(c,a,b)$の場合の$2$通りなので、1回目の交換で交換会が終了する確率は$\color{red}{\dfrac{1}{3}}$です。

（ⅲ）同じく3人で交換会を開く場合を考えます。「4回以下の交換で交換会が終了する」というのは「4回交換しても交換会が終了していない」場合の余事象なので、4回以下の交換で交換会が終了する確率は$$1-\left(\dfrac{2}{3}\right)^{4}=\color{red}{\dfrac{65}{81}}$$と求められます。

（２）で「構想」としてヒントが示されます。

1回目の交換で、4人のうち、ちょうど1人が自分の持参したプレゼントを受け取る場合について、自分のプレゼントを受け取った人以外の3人はプレゼントを交換できているので、先ほど（ⅱ）で考えた3人の場合と同様に考えて$2$通りの受け取り方があります。自分のプレゼントを受け取る人の選び方が4人分で4通りなので計$8$通りと分かります。

ちょうど2人が自分の持参したプレゼントを受け取る場合、自分のプレゼントに当たった人以外については（ⅰ）と同様に考えて$1$通りの受け取り方があります。自分の持参したプレゼントを受け取る人の選び方は ${ }_{4} \mathrm{C}_{2}=6$ 通りなので、計$6$通りと分かります。

ちょうど3人が自分のプレゼントを受け取る場合というのはあり得ない（その時は全員が自分のプレゼントに当たる）ので、4人全員が自分のプレゼントを受け取る場合が$1$通りあります。

以上から、参加者が4人のときの受け取り方のうち、1回目の交換で交換会が終了しない受け取り方の総数は $8+6+1=\color{red}{15}$ 通りと求められます。

したがって、1回目の交換で交換会が終了する場合の数が $4!-15=9$ 通りなので、その確率は $\dfrac{9}{4!}=\color{red}{\dfrac{3}{8}}$ と求められます。

※4人で交換会を開く場合、プレゼントの配られ方の総数は$4!$通りです。

（３）以降は参加者が5人になります。（２）のヒントを上手く使いましょう。

まずは5人のうち1人が自分の持参したプレゼントを受け取る場合を考えます。このとき自分のプレゼントを受け取った人以外の4人はプレゼントを交換できており、4人でプレゼント交換する場合に相当するので$9$通りの受け取り方があります。自分のプレゼントを受け取る人の選び方が5通りなので計$45$通りあります。

5人のうち2人が自分の持参したプレゼントを受け取る場合、自分のプレゼントに当たった人以外については同様に考えて$2$通りの受け取り方があります。自分の持参したプレゼントを受け取る人の選び方は ${ }_{5} \mathrm{C}_{2}=10$ 通りなので、計$20$通りです。

5人のうち3人が自分の持参したプレゼントを受け取る場合、自分のプレゼントに当たった人以外については同様に考えて$1$通りの受け取り方があります。自分の持参したプレゼントを受け取る人の選び方は ${ }_{5} \mathrm{C}_{3}=10$ 通りなので、計$10$通りです。

5人のうち4人が自分の持参したプレゼントを受け取ることは有り得ないので、残るは5人全員が自分のプレゼントを受け取る場合の$1$通りだけです。

以上より、参加者が5人のときの受け取り方のうち、1回目の交換で交換会が終了しない受け取り方の総数は $45+20+10+1=76$ 通りと求められます。余事象を考えると、このとき1回目の交換で交換会が終了する確率は $\dfrac{5!-76}{5!}=\color{red}{\dfrac{11}{30}}$ となります。

ここまで、解説のためにかなり丁寧に説明を書いてきましたが、以上の内容は計算用紙か余白に走り書き程度に（ただし見直しはできるように）メモしておけば良いと思います。

（４）は条件付き確率のオマケ問題です。条件付き確率は毎年のように出題されていますね。

「A,B,C,Dがそれぞれ自分以外の人の持参したプレゼントを受け取る場合」というのはどういうときかというと、「① A,B,C,D,Eがそれぞれ自分以外の人の持参したプレゼントを受け取る場合」と「② Eだけが自分の持参したプレゼントを受け取る場合」の和事象になっています。

まず①の総数について。（３）の考察から、参加者が5人のときに1回の交換で交換会が終了しない受け取り方の総数は$76$通りと分かっています。これ以外の場合が①に相当するので、余事象を考えて$44$通りと分かります。

次に②の総数ですが、Eだけが自分のプレゼントを受け取る場合の確率は（３）で考えた通り$9$通りです。

よって、A,B,C,Dがそれぞれ自分以外の人の持参したプレゼントを受け取る確率は $\dfrac{44+9}{5!}$ であり、参加者が5人のときに交換会が1回で終了する確率は $\dfrac{44}{5!}$ となるので、求める条件付き確率は$$\dfrac{\dfrac{44}{5!}}{\dfrac{44+9}{5!}}=\dfrac{44}{53}$$となります。

確率や数え上げの得意な人は良いのですが、完答までそこそこ手間の掛かる問題だったかと思います。決して悪い問題ではありません。樹形図などでゴリ押しした人もいたようですが、できるだけ効率的に数え上げられるよう普段から訓練しておくべきですね。

数学ⅠＡ第４問

剰余絡みの整数問題です。題材は1次不定方程式の割に、係数が巨大で機械的には解きにくいタフな問題でした。

（１）$$5^{4} x-2^{4} y=1 \quad \cdots ①$$と係数に指数が乗っている不気味な見た目をしています。

$5^4=625$ を$2^4$で割ったときの余りは$1$に等しいことを用いるよう指示がありますが、ヒントになっているような気がしないという人も多かったかもしれませんね…。

ヒントに従うと、$625=2^4 \times 39 +1$ より、$$\left(2^{4} \times 39+1\right) x-2^{4} y=1$$ $$\therefore x-2^{4}(y-39x)=1$$と変形できます。ここで見やすさのために $Y=y-39x$ と置くと、方程式①は$$x-16Y=1 \quad \cdots ①^{\prime}$$と非常に簡単な形になります。ここまでくれば、$x$が正の整数で最小になるのは $\color{red}{x=1}$、$Y=0$（$\color{red}{y=39}$）のときであることが分かります。

次に$x$が2桁の正の整数で最小になる場合を考えます。$①^{\prime}$を $x=16Y+1$ と変形すると、$x$は$16$で割った余りが$1$であるような整数になることが分かります。このことから求める整数解は $\color{red}{x=17}$、$Y=1$（$\color{red}{y=664}$）と求められます。

管理人は最初 $Y=y-39$ と$x$を抜かして計算してしまい、無駄な時間を使ってしまいました…。

（２）は（３）のヒントとなっています。$625=5^4$ なので $625^2=5^8$ は直ちに分かりますね。

いま、$m=39$ です。$625^2$をいきなり$m$の冪で展開しても良いですが、（１）の考察から $625=16 \cdot 39+1$ が分かっているので、これを2乗するのが良いでしょう。2乗すると$$625^2=2^8 m^2+2^5 m+1$$を得ます。その直後の文章は（３）を解いていくと意味が理解できます。

（３）では係数の指数が$5$に変わっています。$$5^5 x-2^5 y=1 \quad \cdots ②$$問題文にごちゃごちゃ書いてありますが、要は何らかの整数$z$を用いて$$5^5 x-625^2=5^5 \cdot 2^5 z \quad \cdots ③$$と表せるということを言っています。$③$の両辺を$5^5$で割り、$$x-5^3=2^5 z$$ $$\therefore x=32z+125 \quad \cdots ③^{\prime}$$と$x$について解きます。$②$の整数解のうちで$x$が3桁の正の整数で最小になるのは$③^{\prime}$式より $z=0$ のときで、このとき $x=\color{red}{125}$ です。これより、$②$式から $y=\dfrac{5^8-1}{2^5}$ となることが分かります。ここで（２）のヒントが効いてきます。$$5^8=625^2=2^8 m^2+2^5 m+1$$ですから、$$\begin{aligned} y &=\frac{\left(2^{8} m^{2}+2^{5} m+1\right)-1}{2^{5}} \\ &=2^{3} m^{2}+m \\ &=8 \cdot 39^{2}+39 \\ &=\color{red}{12207} \end{aligned}$$と、そこまで煩雑でない計算で求められます。ここで誘導に上手く乗れず、5のべき乗を延々と計算した人もいたことと思います。

（４）では$$11^5 x-2^5 y=1$$と今までとは違う方程式が出てきました。上手い方法が思いつかなければ、前問までとの関連性が無いか調べて時間を使うのは得策ではないと判断して、普通の1次不定方程式の要領（特殊解を見つけて辺々引く）で解くこともできます。

まずは誘導に乗る正攻法で解いてみます。問題文中のヒントから、$$11^4=2^4 k +1$$となるようです（実際には $k=915$ となります）。ここで（２）に倣って$11^4$の2乗を考えると、$$11^8=2^8 k^2+2^5 k+1 \quad \cdots ④$$を得ます。ここからは（３）と同じ要領です。（３）の議論と同様にして、ある整数$w$を用いて$$11^5 x-11^8=11^5 \cdot 2^5 w \quad \cdots ⑤$$と表せることが分かります。これより$$x=2^5 w+11^3=32w+1331$$が得られるので、$w=-41$ として $x=\color{red}{19}$ を得ます。よって$$\begin{aligned}
y &=\dfrac{11^{5} \cdot 19-1}{2^{5}} \\
&=\color{red}{95624}
\end{aligned}$$を得ます。関係式$④$も$⑤$も$x$の値によらず成立するので、つい使いたくなりますがあまり計算の省力化には繋がりません。そもそも、$k$を求めることになると$k$と文字で置いたメリットが失われるので、$11^{5} \cdot 19$は余計なことを考えずに筆算で求めるのが良いでしょう…。上手い方法をご存じの方は是非コメント欄にて教えて下さい！

一応、誘導を無視する解法についても触れておきます。

問題文中のヒントを踏まえて、初めに$$11^4=2^4 \cdot 915 +1$$を計算しておきます。これより$$11^5=2^4 \cdot 11 \cdot 915 +11$$となります。これを与方程式に代入して$$(2^{4}\cdot 11 \cdot 915+11) x-2^{5} y=1$$ $$\therefore 11 x-2^{4}(2 y-11 \cdot 915 x)=1$$ここで $Z=2 y-11 \cdot 915 x$ と置くと、$$11x-16Z=1 \quad \cdots ⑥$$となります。ここで$Z$が任意の整数の範囲で動けるとすると、$x=3$、$Z=2$ を得るので、$11 \cdot 3-16 \cdot 2=1$ を$⑥$の両辺から引いて$$11(x-3)-16(Z-2)=0$$を得るので、適当な整数$j$を用いて$$\left\{\begin{array}{l}x=16 j+3 \\ Z=11 j+2\end{array}\right.$$と表せることが分かります。ただし、このとき$x$はあらゆる$j$に対して奇数となるので、$Z=2 y-11 \cdot 915 x$ より$Z$も常に奇数となります。したがって$j$もまた奇数でなければなりません。このことに注意すると $j=1$ のとき$x$は最小の正の整数解となり、$x=19$、$Z=13$ より、$y=95624$ と求められます（計算は頑張る）。

記述式試験だともう少し色々と気を遣う必要がありますが、マーク欄を埋めるだけなら以上の内容を雑に計算するだけで良いでしょう。

それにしても1次試験としてはタフな問題でした。整数分野が得意でも試験場では焦ったという人は多かったのではないでしょうか？

（2022/02/03追記）本問の一般解について考察してみました。

k^5*x-2^5*y=1の整数解（2022年共テ数ⅠＡ第4問）

数学ⅠＡ第５問

今回のセットで個人的に一番解きやすかったのがこの平面図形の問題です。メネラウスの定理を正しく使うことができれば満点を狙えます。

（１）は点$\mathrm{D}$が線分$\mathrm{AG}$の中点であることに注意すれば問題ないでしょう。比の和 $\dfrac{\mathrm{BP}}{\mathrm{AP}}+\dfrac{\mathrm{CQ}}{\mathrm{AQ}}$ は少し目新しい感じがしますが、こちらは点$\mathrm{E}$が線分$\mathrm{BC}$の中点であることに注意すれば $\mathrm{EC}=\mathrm{BE}=\dfrac{1}{2}\mathrm{BC}$ を使って $\color{red}{4}$ と求められます。

（２）もそれほど複雑ではありません。

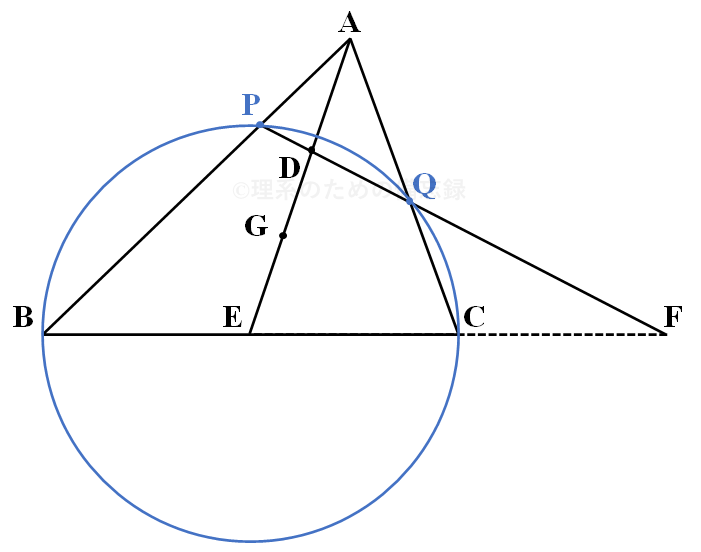
方べきの定理から比が分かり、$\dfrac{\mathrm{BP}}{\mathrm{AP}}+\dfrac{\mathrm{CQ}}{\mathrm{AQ}}=4$ について$\mathrm{AP}$以外の線分の長さをすべて$\mathrm{AP}$で表せば $\mathrm{AP}=\dfrac{13}{6}$ がすぐに求められます。$\mathrm{CF}$はメネラウスの定理から得られる式に $\mathrm{EF}=4+\mathrm{CF}$ を代入して$\mathrm{CF}$について解けばOK。

（３）は着眼が少し難しいかもしれません。（１）では$$\left\{\begin{array}{l}
\dfrac{\mathrm{BP}}{\mathrm{AP}}=2 \times \dfrac{\mathrm{BF}}{\mathrm{EF}} \\
\dfrac{\mathrm{CQ}}{\mathrm{AQ}}=2 \times \dfrac{\mathrm{CF}}{\mathrm{EF}}
\end{array}\right.$$と求められました。この「$2$」の部分は $\dfrac{\mathrm{AD}}{\mathrm{DE}}=\dfrac{1}{2}$ に由来しています。そこで、$$\begin{aligned}
& \dfrac{\mathrm{BF}}{\mathrm{EF}}+\dfrac{\mathrm{CF}}{\mathrm{EF}} \\
=& \dfrac{2 \mathrm{BE}+\mathrm{CF}}{\mathrm{BE}+\mathrm{CF}}+\dfrac{\mathrm{CF}}{\mathrm{BE}+\mathrm{CF}} \\
=& \dfrac{2(\mathrm{BE}+\mathrm{CF})}{\mathrm{BE}+\mathrm{CF}} \\
=& 2
\end{aligned}$$に注目すれば、比 $\dfrac{\mathrm{AD}}{\mathrm{DE}}$ が$\dfrac{1}{5}$であれば常に $\dfrac{\mathrm{BP}}{\mathrm{AP}}+\dfrac{\mathrm{CQ}}{\mathrm{AQ}}=10$ が達成できそうです。したがって、$\dfrac{\mathrm{AD}}{\mathrm{DE}}=\dfrac{1}{5}$ のとき$\dfrac{\mathrm{AD}}{\mathrm{DG}}=\dfrac{1}{3}$ となり、これが答えになります。第5問は素直な問題という印象を受けました。

以上、今年（2022年）の共通テスト数学ⅠＡを一通り解いてみましたが、内容は決して易しくはなく、しかもかなりのボリュームで、2日目の体力をこの1科目で持っていかれてもおかしくない内容でした。

「思考力を問う」と謳っているだけあって教育的な問題ではあるものの、全体の分量が例年になく多いセットとなりました。試験直後に泣き出す生徒がいたり、問題冊子を破り捨てた生徒がいたり(？)と、誇張はあるかもしれませんがそれだけ厳しい試験だったということでしょう。駿台予備学校とベネッセコーポレーションが運営するデータネットの予想平均点が38点（速報値）を叩き出すなど受験界隈は荒れ模様です。

中堅以下の大学では今回の数学ⅠＡではあまり差が付かないのではないかと思います。詳細なデータを見ないことには分かりませんが、難関大志望者の間でも点数の振るわなかった人は少なくないでしょう。全体的に難化傾向のようですし、2次試験の足切りの点数（ボーダーライン）は例年より低くなると予想されます。受験生の皆さんは気持ちを切り替え、2次試験の勉強に集中して取り組んで下さい！

（2022/01/26追記）2022年共通テスト数学ⅡＢについても雑感をまとめました。今回の共通テストに関する私見もコメントで触れています。

2022年共通テスト数学ⅡＢの解説と雑感