今年も受験シーズンがやってきました。受験生の皆さん、まずは共通テストお疲れ様でした。持てる力を存分に発揮できたことと思います。本稿では今年2023年の共通テスト数学ⅠAを解説していきます。管理人が問題を解いた際の雑感なども書き連ねていきます。
※数学ⅡBはこちらから。
全体の概観
昨年(2022年1月)の共通テスト数学ⅠAの平均点は37.96点と久しぶりの30点台という酷い有様でした。今年はというと、最終的な平均点は55.65点となり、数字の上では前年比+17.69点という大幅な易化となりました。実際、時間が全く足りないというタイプの試験問題ではなく、全体的にバランスの良い構成だったと思います。
昨年の反省を踏まえて、以下では、1題ずつ解説を紹介した後に管理人の雑感を簡単に述べるという形にしたいと思います。問題文は掲載していませんので、適宜お手元に用意してください。
※問題はこちらから閲覧できます。(大学入試数学問題集成様より)
目次
・数学ⅠA第1問〔1〕【数と式】
・数学ⅠA第1問〔2〕【平面図形・空間図形】
・数学ⅠA第2問〔1〕【データの分析】
・数学ⅠA第2問〔2〕【2次関数】
・数学ⅠA第3問【場合の数】
・数学ⅠA第4問【整数】
・数学ⅠA第5問【平面図形】
数学ⅠA第1問〔1〕【数と式】
$|x+6| \leqq 2$ の解は, $-2 \leqq x+6 \leqq 2$ より, $$\color{red}{-8 \leqq x \leqq-4}$$となる。(解答欄ア~エ)
$(1-\sqrt{3})(a-b)(c-d)$を$x$と見なせば前問の結果が利用できる。$1-\sqrt{3}<0$ なので不等号が反転することに注意し、$$\color{red}{2+2 \sqrt{3} \leqq(a-b)(c-d) \leqq 4+4 \sqrt{3}}$$を得る。(解答欄オ~ク)
以下、$$\begin{cases}(a-b)(c-d)=4+4 \sqrt{3} \\ (a-c)(b-d)=-3+\sqrt{3}\end{cases}$$が仮定として与えられているので、これら2式の左辺を展開して$$\begin{cases}a c-a d-b c+b d=4+4 \sqrt{3} & \cdots ① \\ a b-a d-b c+c d=-3+\sqrt{3} & \cdots ②\end{cases}$$を得る。$①-②$より$$\begin{aligned} a c-a b+b d-c d & =(a-d)(c-b) \\ & =(4+4 \sqrt{3})-(-3+3 \sqrt{3}) \\ & =\color{red}{7+3 \sqrt{3}}\end{aligned}$$と求められる。(解答欄ケ、コ)
〔1〕は不等式に関する計算問題でした。登場する文字が多いですが、特段難しいという訳ではありませんでした。
数学ⅠA第1問〔2〕【図形と計量】
正弦定理を用いると $\dfrac{\mathrm{AB}}{\sin \angle \mathrm{ACB}}=2 \cdot 5$ となるので、$\sin \angle \mathrm{ACB}=\color{red}{\dfrac{3}{5}}$ である。$\angle \mathrm{ACB}>90^{\circ}$ のとき余弦は負なので、$\cos \angle \mathrm{ACB}=\color{red}{-\dfrac{4}{5}}$ と求められる。(解答欄サ、シ)
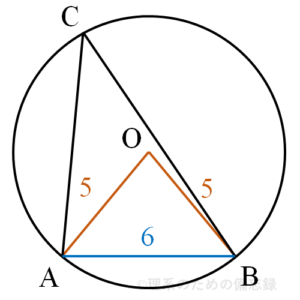
※あるいは、$\mathrm{AB}$の中点を$\mathrm{M}$として、円周角の定理を用いて直角三角形$\mathrm{AOM}$から$$\sin \angle \mathrm{ACB}=\sin \angle \mathrm{AOM}=\dfrac{3}{5}$$として求めても良い。
$\triangle \mathrm{ABC}$の面積が最大となるのは点$\mathrm{C}$と直線$\mathrm{AB}$距離が最も大きくなるときであるから、$\angle \mathrm{ABC}$が鋭角で、かつ$\triangle \mathrm{ABC}$が二等辺三角形となるときである。よって、$\tan \angle \mathrm{OAD}=\color{red}{\dfrac{4}{3}}$、$\triangle \mathrm{ABC}=\dfrac{1}{2}\cdot 6 \cdot 9 = \color{red}{27}$ と求められる。(解答欄ス~ソ)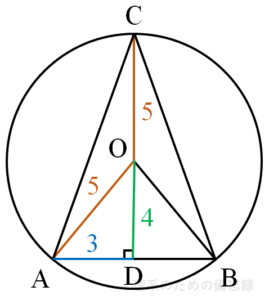
ここまでは単純な三角比の計算問題でした。(2)からは空間図形の問題になります。
$\triangle \mathrm{PQR}$に対して余弦定理を用いると $$\begin{aligned} \cos \angle \mathrm{QPR} &=\frac{9^2+8^2-5^2}{2 \cdot 9 \cdot 8} \\ &=\dfrac{5}{6}\end{aligned}$$となり、$$\sin \angle \mathrm{QPR}=\sqrt{1-\left(\frac{5}{6}\right)^2}=\frac{\sqrt{11}}{6}$$となる。したがって$\triangle \mathrm{PQR}$の面積は$$\begin{aligned} \triangle \mathrm{PQR} & = \dfrac{1}{2} \cdot 9 \cdot 8 \cdot \sin \angle \mathrm{QPR} \\ &=36 \cdot \dfrac{\sqrt{11}}{6} \\ &=\color{red}{6 \sqrt{11}}\end{aligned}$$となる。(解答欄タ~ト)
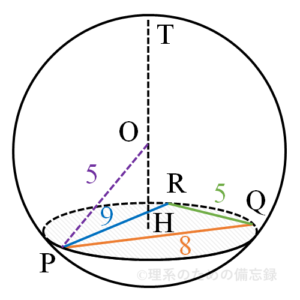
三角錐$\mathrm{TPQR}$の体積が最大となるのは点$\mathrm{T}$と平面$\mathrm{PQR}$(平面$\alpha$)との距離が最も大きくなるときであり、このとき点$\mathrm{H}$は$\triangle \mathrm{PQR}$の外心となる。よって$$\color{red}{\mathrm{PH}=\mathrm{QH}=\mathrm{RH}}$$が成り立つ。ここで$\triangle \mathrm{PQR}$に対して正弦定理を用いると$$\dfrac{\mathrm{QR}}{\sin \angle \mathrm{QPR}}=2 \mathrm{PH}$$ $$\therefore \mathrm{PH}=\dfrac{5}{2 \cdot \dfrac{\sqrt{11}}{6}}=\dfrac{15}{\sqrt{11}}$$を得る。よって三角錐$\mathrm{TPQR}$の体積$V$は$$\begin{aligned} V &= \dfrac{1}{3} \cdot 6 \sqrt{11} \cdot\left\{5+\sqrt{5^2-\left(\dfrac{15}{\sqrt{11}}\right)^2}\right\} \\ &=2 \sqrt{11}\left(5+5 \sqrt{\dfrac{2}{11}}\right) \\ &=\color{red}{10\left(\sqrt{11}+\sqrt{2}\right)} \end{aligned}$$と求められる。(解答欄ナ~ハ)
$\triangle \mathrm{PQR}$の3辺の長さが分かっているので面積を求めるところまでは問題ないと思います。正弦定理から$\triangle \mathrm{PQR}$の外接円の半径$\mathrm{PH}$を求めるところがやや難しいでしょうか。愚直な計算が求められる共通テストらしい出題でした。
数学ⅠA第2問〔1〕【データの分析】
まず下図のように、各データの値(下側赤字)、データ値の累積(上側青字)、四分位範囲(上側緑字)を計算する。
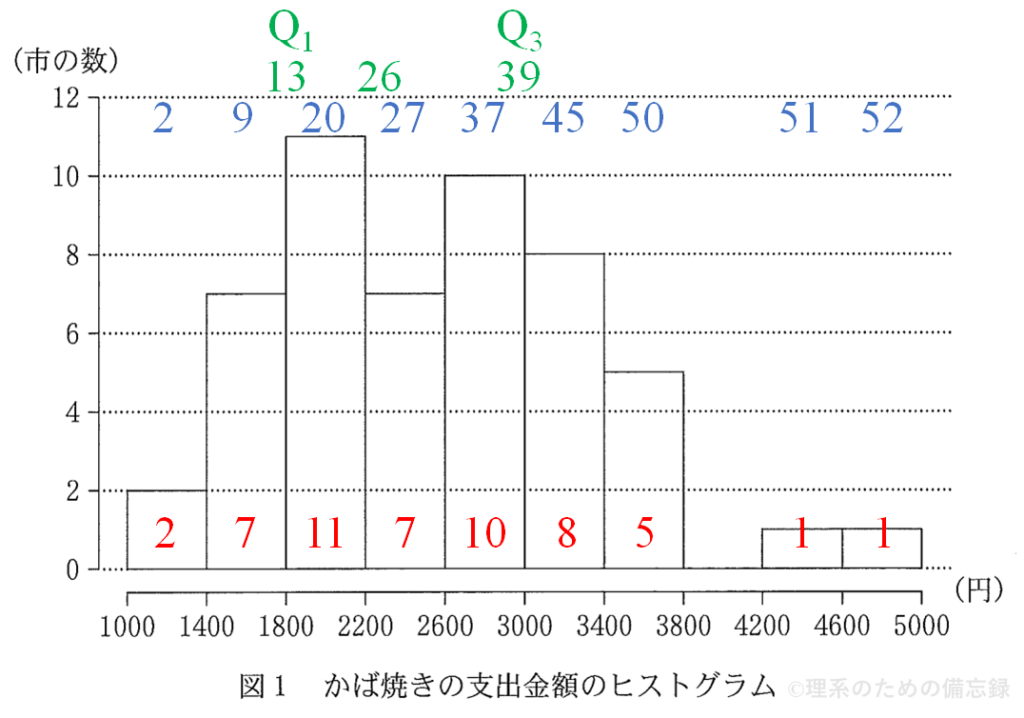
これより、第1四分位数が含まれる階級は「② 1800以上2200未満」、第3四分位数が含まれる階級は「⑤ 3000以上3400未満」と分かる。また、$1800 \leqq Q_1 < 2200$ および $3000 \leqq Q_3 < 3400$ より、$$800<Q_3-Q_1<1600$$となるので、四分位範囲は「① 800より大きく1600より小さい」。(解答欄ア~ウ)
基本的な問題です。
(下図は問題文に示されている箱ひげ図である)
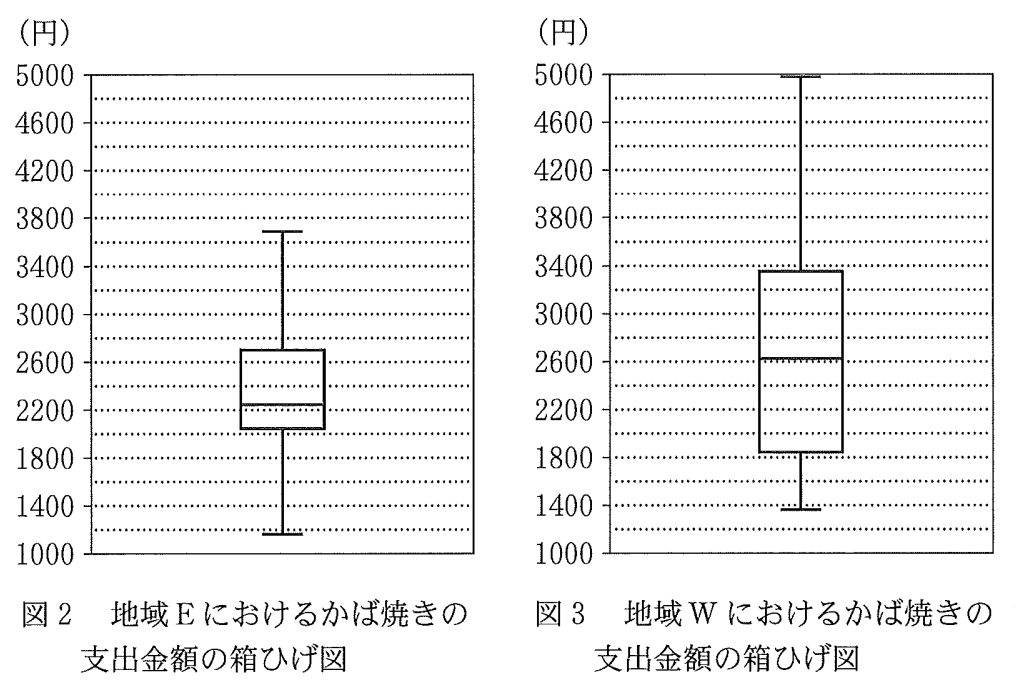
設問(i)は②が正答である。(解答欄エ)
⓪について、地域Eの第1四分位数は2000を上回っているため、小さい方から5番目は2000以上である可能性が排除できないので不適。
①について、地域Eと地域Wのデータの範囲は明らかに等しくないので不適。
③について、地域Eの第3四分位数と地域Wの中央値が同程度であることに注目すると、地域Wの方が2600未満の市の割合が多いとは言えない。
(ii)は分散の定義を問う問題である。偏差$s$に対して分散は$$s^2 = \dfrac{1}{n}\displaystyle \sum_{i=1}^{n} (x_i-\bar{x})^2$$で与えられる。選択肢は「② 2乗を合計して地域Eの市の数で割った値」となる。(解答欄オ)
要点を押さえられていれば、特に躓く点は無いと思います。
相関係数$r$は以下の式で与えられる。$s_{xy}$を$x$と$y$の共分散、$s_x$と$s_y$をそれぞれ$x$、$y$の標準偏差として$$r=\dfrac{s_{xy}}{s_x s_y}$$各値は既に表で与えられているので、これらを用いる。この設問では大まかな値を選べばよいので、各値を大雑把に丸めて概算すればよい。$$r \fallingdotseq \dfrac{124000}{590 \times 570} \fallingdotseq \dfrac{1240}{60 \times 60} \fallingdotseq \dfrac{1}{3}$$よって、これに最も近い「⑦ $0.37$」を選べばよい。(解答欄カ)
「データの分析」の単元としては、昨年に比べてかなり平易な問題でした。相関係数については、データ点のバラつきから0.5よりは小さいと判断して、大雑把に目視で見積もった人もいたかも知れませんね…😅
数学ⅠA第2問〔2〕【2次関数】
放物線$C_1$は2点$(0,3)$、$(4,3)$を通るので、まず定数項は「ク:$3$」と分かる。$(4,3)$を方程式に代入すると、$$16a-4\cdot\boxed{ キ }\cdot a=0$$となるので$$\boxed{ キ }=4$$と分かる。よって$$C_1:\color{red}{y=ax^2-4ax+3}$$であり、これを平方完成すると$$y=a(x-2)^2-4a+3$$となるので、「シュートの高さ」は $\color{red}{-4a+3}$ と求められる。(解答欄キ~コ)
問題文中の放物線$C_2$の方程式から、花子さんの「ボールが最も高くなるときの地上の位置」は $x=2-\dfrac{1}{8 p}$、「シュートの高さ」は $-\dfrac{(16 p-1)^2}{64 p}+2$ で与えられる。
選択肢⓪は $2-\dfrac{1}{8 p}=2$ が成り立つという主張だが、これは明らかに成り立たないので正しくない。
選択肢①は $4-\left(2-\dfrac{1}{8 p}\right)>2$ が成り立つという主張だが、$p<0$ より $2-\dfrac{1}{8 p}>2$ なので、これも正しくない。
選択肢②は正答である。(解答欄サ)
選択肢③は $2-\dfrac{1}{8 p}$ が常に$2$より大きいことから正しくないと分かる。
やや目新しい設定の問題でした。誘導がかなり丁寧なので、計算ミスにだけ注意したいですね。
$\mathrm{AD}=\dfrac{\sqrt{3}}{15}$ より、放物線$C_1$は点$\left(\dfrac{38}{10}, 3+\dfrac{\sqrt{3}}{15}\right)$を通る。これを放物線$C_1$の方程式に代入して整理し、$$3+\dfrac{\sqrt{3}}{15}=\left(\dfrac{38}{10}\right)^2 a-4\cdot \dfrac{38}{10}a+3$$ $$\therefore \dfrac{\sqrt{3}}{3}=\dfrac{19^2}{5}a-4\cdot 19a$$ $$\therefore \dfrac{\sqrt{3}}{3}=-\dfrac{19}{5}a$$ $$\begin{aligned} \therefore a&=-\dfrac{5}{19} \cdot \dfrac{\sqrt{3}}{3} \\ &=\color{red}{-\dfrac{5\sqrt{3}}{57}} \end{aligned}$$を得る。(解答欄シ~ソ)
「プロ選手のシュートの高さ」は $-4a+3$ で与えられるから、$a=-\dfrac{5\sqrt{3}}{57}$ を代入して$$\dfrac{20\sqrt{3}}{57}+3$$となる。問題文より「花子さんのシュートの高さ」は約$3.4$と与えられているので、$\dfrac{20\sqrt{3}}{57}$と$0.4$の大小を比較すればよい。$\sqrt{3} \approx 1.7$ とすると$$\dfrac{20\sqrt{3}}{57} \approx \dfrac{34}{57} \approx 0.6$$となる。実際には $\sqrt{3}>1.7$ なので、「プロ選手のシュートの高さ」は$3.6$より多少大きい程度である。したがって、「プロ選手(解答欄タ:選択肢⓪)」の方が「シュートの高さ」が大きく、その差はボール「約1個分(解答欄チ:選択肢⓪)」と分かる。
数式の見かけは複雑そうですが、落ち着いて丁寧に計算すればOKです。最後の概算が大雑把すぎて不安だという人は小数点以下第2位まで考慮した $1.73$ という近似値を使ってもよいですが、計算結果は$0.607$とあまり変わりません。また、左ページに会話が示されていますが、これは軽く読み飛ばしても解答にはあまり支障がありませんでした。
数学ⅠA第3問【場合の数】
(下図は問題文に示されている球の繋ぎ方である)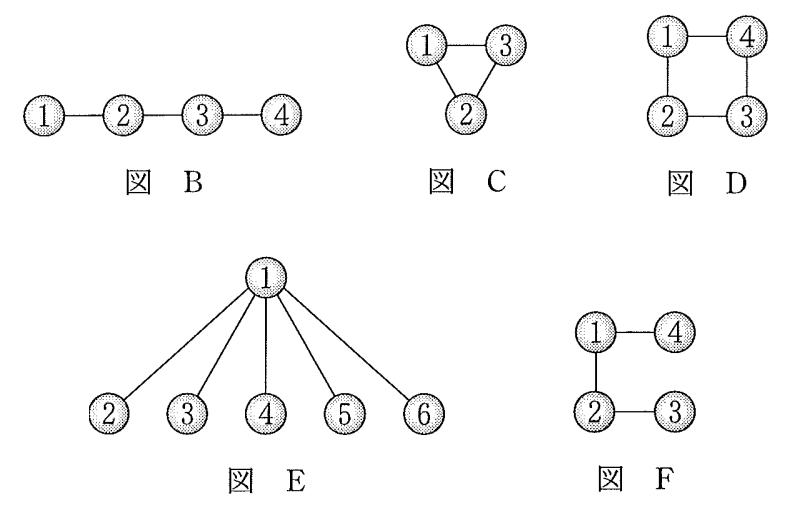
(1)
図Bについて①→②→③→④と色を塗っていく方法を考えると、①は5通り、②は①以外の色で4通り、③は②以外の色で4通り、④は③以以外の色で4通りとなり、総数は$$5 \times 4 \times 4 \times 4=\color{red}{320}$$となる。(解答欄ア~ウ)
(2)
図Cについて①→②→③と色を塗っていく方法を考えると、①は5通り、②は①以外の色で4通り、③は①と②以外の色で3通りとなり、総数は$$5 \times 4 \times 3=\color{red}{60}$$となる。(解答欄エ~オ)
(3)
図Dについて、赤を2回使うのは「あ)①と③に赤を塗る」または「い)②と④に赤を塗る」の場合に限られる。
あ)のとき、②と④の色の塗り方は、赤以外の色を塗ればよいから $4 \times 4=16$ 通りである。
い)のとき、①と③の色の塗り方は、あ)の場合と同様に $16$ 通りである。
よって求める場合の数は$$16+16=\color{red}{32}$$となる。(解答欄カ~キ)
(4)
図Eにおいて、赤を3回、青を2回使う場合、まず①は赤と青以外の色を塗らなければならないので $3$ 通り。②~⑥の色の塗り方は ${ }_5 \mathrm{C}_3 \times{ }_2 \mathrm{C}_2=10$ 通りであるから、色の塗り方は$$3 \times 10=\color{red}{30}$$となる。(解答欄ク~ケ)
(5)
図Fにおいて、色の塗り方は図Bと共通であり、③と④が同じ色になる場合の数は図Cと共通(選択肢②)で $\color{red}{60}$ 通り。これより、図Dにおける色の塗り方は$$5 \times 4 \times 4 \times 4-60=\color{red}{260}$$となる。(解答欄コ~ス)
(6)
(5)の議論をそのまま利用すると、場合の数について以下の関係が成り立つ。
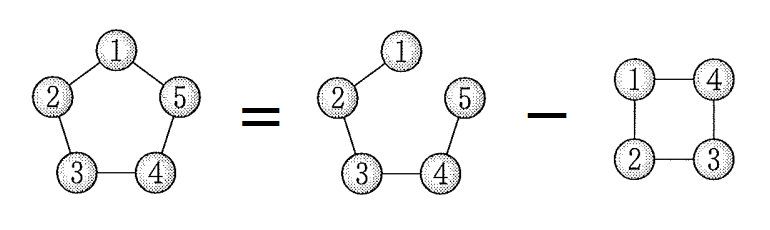
よって、$$5 \times 4 \times 4 \times 4 \times 4-260=\color{red}{1020}$$と求められる。(解答欄セ~チ)
綺麗な誘導が付いている問題でした。上手に誘導に乗れた人は高得点だったと思います。なお、球には番号が付いており、すべての球は区別されています。数珠順列ではないので注意。
数学ⅠA第4問【整数】
$462=2\cdot 3\cdot 7\cdot 11$、$110=2\cdot 5\cdot 11$ より、$462$と$110$の両方を割り切る素数のうち最大のものは$\color{red}{11}$である。(解答欄ア~イ)
以下、$i$と$j$を正の整数として、下図のように赤い長方形を横に$i$枚、縦に$j$枚並べるとする。
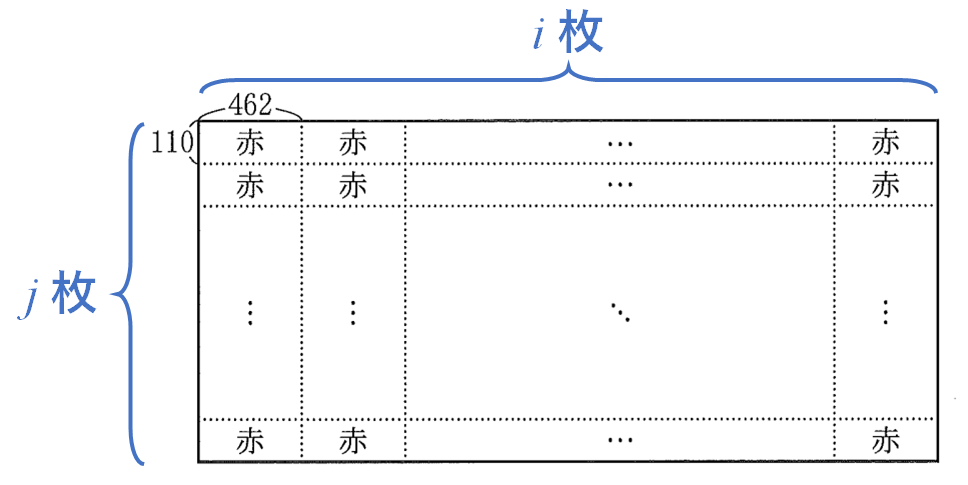
正方形を作るとき、辺の長さについて$$462i=110j$$ $$\therefore 21i=5j$$が成り立つことが必要である。$21$と$5$は互いに素であるから、$i$は$5$の倍数、$j$は$21$の倍数であることが必要となる。このような場合で最小の値は $(i,j)=(5,21)$ であるから、このとき正方形の1辺は最小値 $462 \cdot 5 = \color{red}{2310}$ をとる。(解答欄ウ~カ)
次に、赤い長方形を横に$i$枚、縦に$j$枚並べて正方形ではない長方形を作る。ここで、横の長さと縦の長さの差を$d$として方程式$$462i-110j=d$$を考える。左辺は$22$の倍数であるから$d$も$22$の倍数でなければならない。そこで $d=22d^{\prime}$ と置く($d^{\prime}$は整数)。これより方程式は$$21i-5j=d^{\prime}$$となり、これは $d^{\prime}=1$ のときに整数解 $(i,j)=(1,4)$ をもつ。したがって、$d$が最小となるのは $d=\color{red}{22}$ のときである。(解答欄キ~ク)
また、縦の長さが横の長さよりも$22$だけ長いのは $d^{\prime}=-1$ のときであり、このとき$i$が最も小さい整数解は $(i,j)=(4,17)$ となり、このとき長方形の横の長さは $462 \cdot 4 = \color{red}{1848}$ となる。
問題設定を正しく把握して不定方程式に還元できれば、ごく普通の整数問題です。(2)からは別の長方形が登場します。
下図のように、赤い長方形を縦に$m$枚、横に$x$枚、青い長方形を縦に$n$枚、横に$y$枚並べる。
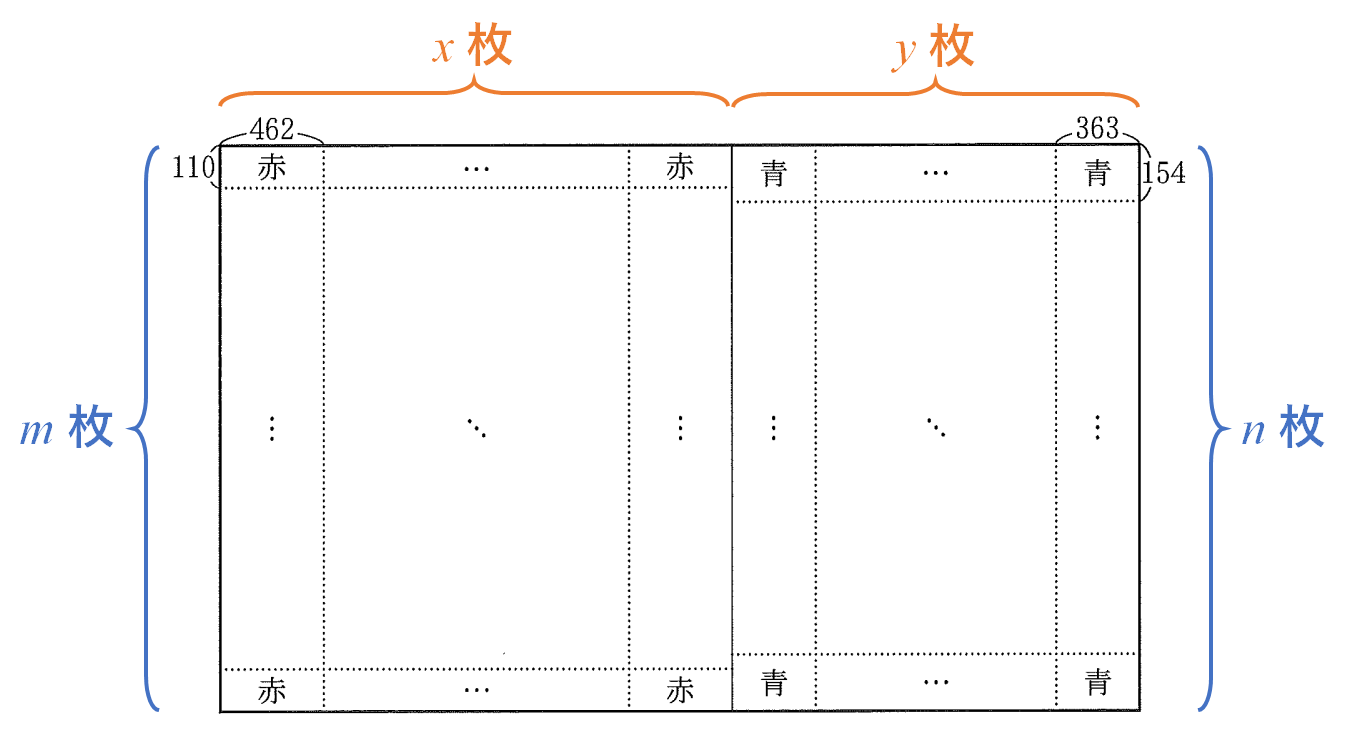
全体が長方形になるとき、縦の長さが一致しなければならないから、$$110m=154n$$ $$\therefore 5m=7n$$が必要となる。$5$と$7$は互いに素であるから、$m$は$7$の倍数、$n$は$5$の倍数でなければならない。これを満たす最小の整数組は $(m,n)=(7,5)$ であり、このとき縦の長さは$\color{red}{770}$となる。(解答欄ス~ソ)
次に、全体が長方形になるときを考える。$462=2\cdot 3\cdot 7\cdot 11$、$363=3\cdot 11^2$ より、$462$と$363$の最大公約数は$\color{red}{33}$であり、$33$の倍数のうちで$770$($=2\cdot 5\cdot 7\cdot 11$)の倍数でもある最小の正の整数は$\color{red}{2310}$である。(解答欄タ~ナ)
上記の内容から、作られる正方形の1辺の長さは$2310$の倍数でなければならないことが分かる。そこで、正方形の横の長さについて、$$462x+363y=2310k$$が成り立つ($k$は正の整数)。この両辺の係数を約分すると$$14x+11y=70k$$となる。これより$y$は$14$の倍数であることが必要で、正の整数$Y$を用いて $y=14Y$ と置ける。よってこの方程式は$$x+11Y=5k$$と書き直すことができる。ここで $x=4$、$Y=1$ のとき $k=3$ となり、このとき辺の長さは最小である。よって求める辺の長さの最小値は$$3\cdot 2310=\color{red}{6930}$$である。(解答欄ニ~ノ)
昨年のような桁数が巨大で煩雑な計算も無く、かなり解きやすかったのではないかと思います。(2)が少しややこしい印象を受けますが、誘導がとても丁寧なので不定方程式を立式する手順には困らないはず。
不定方程式は係数が大きいままだと解を求めにくいので、倍数の制約から置き換えにより係数を小さくしていくのが定石です。(2)の最後は$x$と$y$がともに正という条件の下で、できるだけ小さい$k$を求めることになります。$x+11Y=5k$ の右辺が$5$の倍数なので、左辺ができるだけ小さい$5$の倍数となるように$x$、$Y$の組を決めればOKです。
数学ⅠA第5問【平面図形】
直線$\mathrm{EH}$が円$\mathrm{O}$の接線であることを証明するには、$$\angle \mathrm{OEH}= \color{red}{90^{\circ}}$$を示せばよい。(解答欄ア~イ)
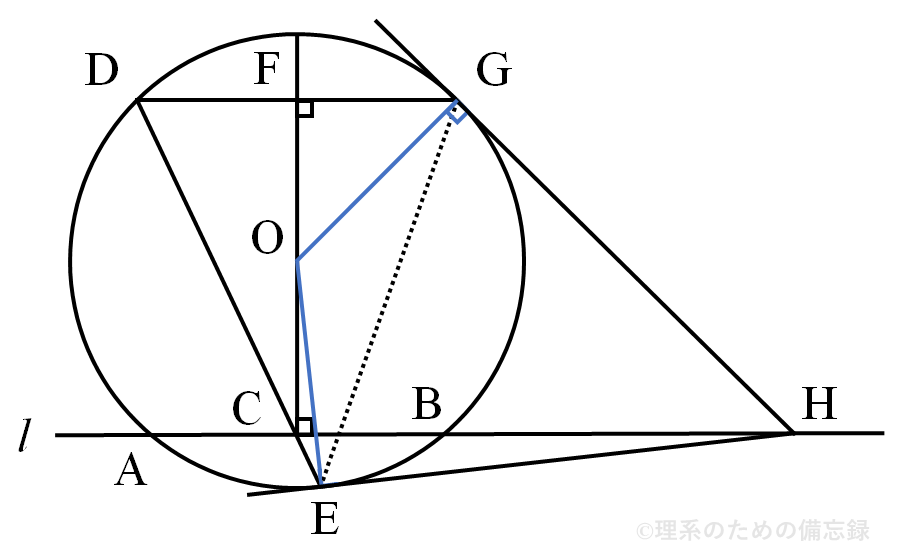
$\angle \mathrm{OCH}=\angle \mathrm{OGH}=90^{\circ}$ より、4点$\mathrm{C}$、$\mathrm{G}$、$\mathrm{H}$、$\color{red}{\mathrm{O}}$は同一円周上に存在する。よって$\angle \mathrm{CHG}$は対角の外角である$\angle \mathrm{FOG}$に等しいから$$\angle \mathrm{CHG}=\color{red}{\angle \mathrm{FOG}}$$が成り立つ。(解答欄ウ~エ)
また、$\triangle \mathrm{ODG}$が二等辺三角形であることと円周角の定理から$$\angle \mathrm{FOG}=\dfrac{1}{2} \angle \mathrm{DOG}=\color{red}{\angle \mathrm{DEG}}$$が成り立つ。(解答欄オ)
したがって $\angle \mathrm{CHG}=\angle \mathrm{DEG}\,(=\angle \mathrm{CEG})$ より、4点$\mathrm{C}$、$\mathrm{G}$、$\mathrm{H}$、$\color{red}{\mathrm{E}}$は同一円周上に存在する。(解答欄カ)
ここまでは基本的な平面図形の証明問題です。円の中心を通る直線が弦と垂直に交わるとき、この直線は弦の垂直二等分線になります。
問題文の手順2の通りに作図すると以下のようになる。ここで、直線$\mathrm{TS}$の延長に点$\mathrm{U}$をとる。
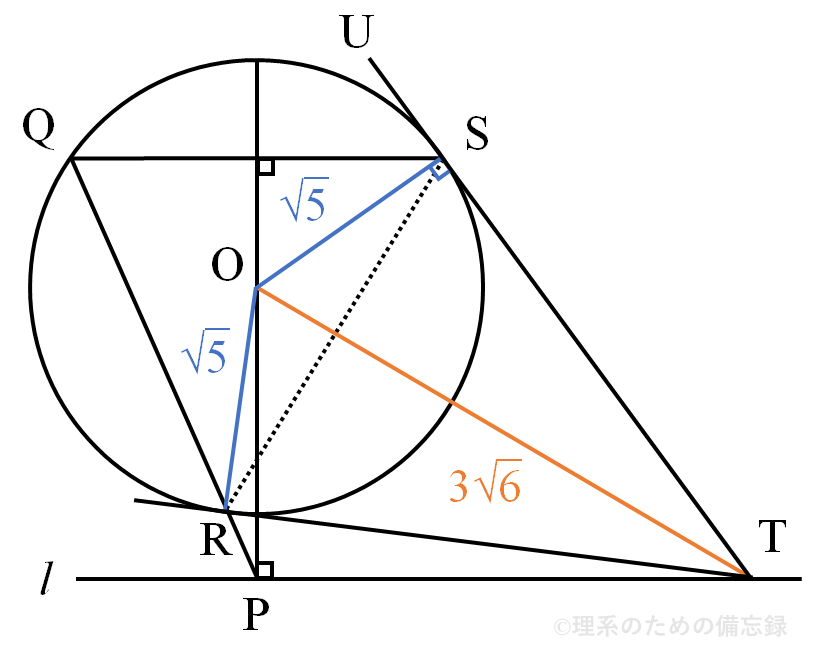
いま、直線$\mathrm{TU}$は点$\mathrm{S}$における円$\mathrm{O}$の接線であるから、接弦定理より$$\angle \mathrm{USQ}=\angle \mathrm{QRS}$$が成り立つ。また、直線$\mathrm{QS}$と直線 $l$ はともに直線$\mathrm{OP}$に対して直交しており互いに平行であるから、同位角の関係より$$\angle \mathrm{USQ}=\angle \mathrm{PTS}$$が成り立つ。したがって、$$\angle \mathrm{PTS}=\color{red}{\angle \mathrm{QRS}}$$が成り立つ。(解答欄キ)
よって、四角形$\mathrm{RPTS}$の外角($\angle \mathrm{QRS}$)がそれと隣り合う内角の対角($\angle \mathrm{PTS}$)に等しいことから、4点$\mathrm{R}$、$\mathrm{P}$、$\mathrm{T}$、$\mathrm{S}$が同一円周上に存在することが従う。
また、(1)と同様に$\angle \mathrm{OPT}=\angle \mathrm{OST}=90^{\circ}$ より、4点$\mathrm{P}$、$\mathrm{T}$、$\mathrm{S}$、$\mathrm{O}$は同一円周上に存在することから、点$\mathrm{R}$もこの円周上に存在している。これより、円周角の定理から $\angle \mathrm{ORT}=90^{\circ}$ と分かるので、直線$\mathrm{RT}$は点$\mathrm{R}$における円$\mathrm{O}$の接線である。
以上より、線分$\mathrm{OT}$は3点$\mathrm{O}$、$\mathrm{P}$、$\mathrm{R}$を通る円の直径であるから、円の半径は $\color{red}{\dfrac{3\sqrt{6}}{2}}$ であり、$\triangle \mathrm{ORT}$について三平方の定理から $\mathrm{RT}=\color{red}{7}$ と求められる。(解答欄ク~サ)
(2)は(1)の考え方を利用する問題でした。直線$\mathrm{RT}$はいかにも接線のような顔をしていますがこのことは自明ではなく、厳密に証明するには上記のようなプロセスを踏む必要があります。思うように解けなかったという人は、点が同一円周上に存在する条件や、四角形が円に内接する条件などをよく復習しておきましょう。また、慌てると作図を間違って時間を無駄にしてしまいます。問題文の手順を丁寧になぞって作図するようにしましょう。
以上、今年(2023年)の共通テスト数学ⅠAを一通り解説しました。今回に関しては昨年のような小言コメントは不要でしょう(笑)。何かと昨年の問題と比較してしまいがちですが、分量や問題の質は全体的にバランスの取れた良い試験だったと思います。今後も、しっかり勉強してきた受験生が報われるような作問に努めていただきたいと思います。

“2023年共通テスト数学ⅠAの解説と雑感” への1件の返信