2023年共通テスト数学ⅡＢの解説と雑感

（１）

$x=\dfrac{\pi}{6}$ のとき、$$\sin x=\sin\dfrac{\pi}{6}=\dfrac{1}{2}$$および$$\sin 2x=\sin\dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2}$$となることから、$\sin x \,\color{red}{<}\,\color{black}{\sin 2x}$ が成り立つ。（解答欄ア）

また、$x=\dfrac{2}{3}\pi$ のとき、$$\sin x=\sin\dfrac{2}{3}\pi=\dfrac{\sqrt{3}}{2}$$および$$\sin 2x=\sin\dfrac{4}{3}\pi=-\dfrac{\sqrt{3}}{2}$$となることから、$\sin x \,\color{red}{>}\,\color{black}{\sin 2x}$ が成り立つ。（解答欄イ）

（２）

$$\begin{align}
\sin 2x-\sin x &= 2 \sin x \cos x -\sin x \\
&=\color{red}{\sin x(2\cos x -1)}
\end{align}$$となる。（解答欄ウ、エ）

$\sin x>0$ かつ $2\cos x -1>0$ となるのは「$0<x<\pi$」かつ「$0<x<\dfrac{\pi}{3}$ または $\dfrac{5\pi}{3}<x<2\pi$」のときであるから、求める範囲は$$\color{red}{0<x<\dfrac{\pi}{3}}$$である。

また、$\sin x<0$ かつ $2\cos x -1<0$ となるのは「$\pi<x<2\pi$」かつ「$\dfrac{\pi}{3}<x<\dfrac{5\pi}{3}$」のときであるから、求める範囲は$$\color{red}{\pi<x<\dfrac{5\pi}{3}}$$である。（解答欄オ～キ）

（３）

$\alpha$、$\beta$は$$\begin{cases} \alpha+\beta=4x \\ \alpha-\beta=3x \end{cases}$$を満たすから、辺々を加える、もしくは差を取って、$$\begin{cases} \alpha=\dfrac{7}{2}x \\ \beta=\dfrac{1}{2}x \end{cases}$$と表せる。誘導に従うと、$$\sin 4x-\sin 3x=2\cos\dfrac{7x}{2}\sin \dfrac{x}{2}$$と表せるから、$\sin 4x-\sin 3x>0$ が成り立つためには、$\cos\color{red}{\dfrac{7x}{2}}$ と $\sin \color{red}{\dfrac{x}{2}}$ が同符号であればよい。

問題文より $0 \leqq x \leqq \pi$ であり、このとき $0 \leqq \dfrac{x}{2} \leqq \dfrac{\pi}{2}$ となるから $\sin \dfrac{x}{2}$ は正である。したがって $\cos\dfrac{7x}{2}>0$ の条件を考えればよい。（問題文中の条件④の場合のみを考えればよい）

$\cos\dfrac{7x}{2}>0$ となるのは「$0<\dfrac{7}{2}x<\dfrac{\pi}{2}$ または $\dfrac{3}{2}\pi<\dfrac{7}{2}x<\dfrac{5}{2}\pi$」の場合であり、これより「$\color{red}{0<x<\dfrac{\pi}{7}}$ または $\color{red}{\dfrac{3}{7}\pi<x<\dfrac{5}{7}\pi}$」を得る。（解答欄ク～セ）

（４）

$y=2x$ と置くと $0\leqq y\leqq 2\pi$ となるから、$\sin 2y-\sin y> 0$ となるのは（２）より

$0< y<\dfrac{\pi}{3}$ または $\pi< y<\dfrac{5}{3}\pi$

つまり

$0< x<\dfrac{\pi}{6}$ または $\dfrac{\pi}{2}< y<\dfrac{5}{6}\pi$

のときである。

また（３）から、$\sin 3x>\sin 4x$ となるのは

$\dfrac{\pi}{7}<x<\dfrac{3}{7}\pi$ または $\dfrac{5}{7}\pi<x<\pi$

のときである。以上より、$\sin 3x>\sin 4x>\sin 2x$ を満たすのは

$\dfrac{\pi}{7}< x<\dfrac{\pi}{6}$ または $\dfrac{5}{7}\pi< x<\dfrac{5}{6}\pi$

のときである。（解答欄ソ～チ）

（１）

$a>0$、$a \neq 1$、$b>0$ で、$a^x=b$ のとき $x=\log_a b$ と表すのが対数関数の定義であるから「② $a^x=b$」が正答となる。（解答欄ツ）

（２）

定義より、$\log_5 25=\color{red}{2}$ であり、底の変換公式から $\log_9 27 =\dfrac{\log_3 27}{\log_3 9}=\color{red}{\dfrac{3}{2}}$ となる。

※ $9^{\frac{3}{2}}=27$ に$9$を底とする対数をとってもよい。

$$\log_2 3=\dfrac{p}{q}$$ $$\therefore 2^{p/q}=3$$ $$\therefore \color{red}{2^{p}=3^{q}}$$である。（解答欄ニ：⑤）

$a$と$b$の偶奇が異なる場合、$a^{p}=b^{q}$ を満たすような自然数$p$、$q$は存在しないから、$\log_a b$ はつねに無理数である。（解答欄ヌ：⑤）

（１）

$f(x)=x^2(k-x)$ は$(0,0)$、$\color{red}{(k,0)}$を解にもつ。（解答欄ア：④）

$$\begin{aligned} f^{\prime}(x)&=2x(k-x)-x^2 \\ &=\color{red}{-3x^2+2kx} \\ &=-3x\left(x-\dfrac{2}{3}k\right)\end{aligned}$$であり、$x=\color{red}{0}$ のとき$f(x)$は極小値 $\color{red}{0}$ をとり、$x=\color{red}{\dfrac{2}{3}k}$ のとき$f(x)$は極小値 $\color{red}{\dfrac{4}{27}k^3}$ をとる。（解答欄イ～ク）

（２）

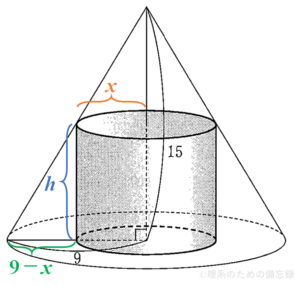
図のように円柱の高さを$h$と置くと、断面となる２つの相似な三角形について$$9-x:h=9:15$$が成り立つから$$\therefore h=15-\dfrac{5}{3}x$$と表せる。よって$$\begin{aligned} V&=\pi x^2 \left(15-\dfrac{5}{3}x\right) \\ &=\color{red}{\dfrac{5}{3}\pi x^2 (9-x)} \end{aligned}$$を得る。（解答欄ケ～サ）

（１）より、$V$は定数倍した$f(x)$において $k=9$ とした場合に相当するから、$x=\dfrac{2}{3}\cdot 9=\color{red}{6}$ のとき最大値 $\color{red}{180 \pi}$ をとる。（解答欄シ～ソ）

（１）

$$\begin{aligned} \displaystyle \int_{0}^{30} \left(\dfrac{1}{5}x+3\right) dx &=\left[\frac{x^2}{10}+3x\right]_0^{30} \\
&=\dfrac{30^2}{10}+3\cdot30 \\
&=\color{red}{180} \end{aligned}$$ $$\begin{aligned} & \quad \int \left(\frac{1}{100}x^2-\frac{1}{6}x+5\right) dx \\ &=\color{red}{\dfrac{1}{300}x^3-\dfrac{1}{12}x^2+5x}+C \end{aligned}$$（解答欄タ～ネ）

（２）

$n$日後に開花するとすると、$$\int_0^n \left(\frac{1}{5}x+3\right) dx = 400$$より、$$\left[\frac{1}{10}x^2+3x\right]_0^n=400$$ $$\therefore \dfrac{n^2}{10}+3n-400 = 0$$ $$\therefore n^2+30n-4000=0$$ $$\therefore (n-50)(n+80)=0$$ $n$は正なので $n=50$ となり、開花するのは「④ 50日後」と分かる。（解答欄ノ：④）

$\displaystyle \int_{0}^{30} \left(\dfrac{1}{5}x+3\right) dx=180$ で、$\displaystyle \int_{30}^{40}\left(\dfrac{1}{100} x^2-\dfrac{1}{6} x+5\right) d x=115$ が分かっているので、あと$105$だけ積分値が増えたら開花することが分かる。

$x \geqq 30$ の範囲では$f(x)$は$$f(x)=\dfrac{1}{100}\left(x-\dfrac{25}{3}\right)^2+\dfrac{155}{36}$$となり二次関数として単調増加する（問題文中②式を平方完成した）。したがって$$\color{red}{\displaystyle \int_{30}^{40} f(x)dx \,(=115)<\int_{40}^{50} f(x)dx}$$が成り立つから、ソメイヨシノは「④ 40日より後、かつ50日より前」に開花する。（解答欄ハ、ヒ）

（１）

$$\begin{aligned} P(x\geqq m)
&=P(x-m\geqq 0) \\
&=P\left(\dfrac{x-m}{\sigma} \geqq \color{red}{0}\color{black}\right) \end{aligned}$$これは標準正規分布に従う確率変数が$0$以上となる確率に相当するから $\color{red}{\dfrac{1}{2}}$ である。（解答欄ア～ウ）

定義に従うと、$E(\bar{X})=\color{red}{m}$、$\sigma(\bar{X})=\color{red}{\dfrac{\sigma}{\sqrt{n}}}$ となる。（解答欄エ、オ）

問題文中の「方針」に従うと、$P(-z_0 \leqq Z \leqq z_0)=0.901$ より $P(0 \leqq Z \leqq z_0)=0.4505$ となる。よって正規分布表から $z_0=\color{red}{1.65}$ と求められる。（解答欄カ～ク）

$z_0=1.65$ より、$$-1.65 \leqq \frac{m-30}{0.18} \leqq 1.65$$が成り立つ。これを整理すると$$29.703 \leqq m \leqq 30.297$$となるから、「④ $27 \leqq m \leqq 30.3$」を選択すればよい。（解答欄ケ）

（２）

$m=30.0$ なので「ピーマン分類法」に従うと、無作為に１個抽出したピーマンがSサイズである確率は $\color{red}{\dfrac{1}{2}}$ となる。$25$袋作るので、$$\begin{aligned} p_0 &= {}_{50}\mathrm{C}_{\color{red}{25}} \cdot\left(\frac{1}{2}\right)^{25} \cdot\left(1-\frac{1}{2}\right)^{25} \\
&={}_{50}\mathrm{C}_{25} \cdot \frac{1}{2^{50}} \end{aligned}$$と表せる。（解答欄コ～ス）

ピーマンを $50+k$ 個抽出したときのSサイズの個数$U_k$は、二項分布 $B\left(50+k,\,\dfrac{1}{2}\right)$ に従う。よって、平均は $\dfrac{50+k}{2}$、分散は $(50+k)\cdot \dfrac{1}{2}\cdot\left(1-\dfrac{1}{2}\right)=\dfrac{50+k}{4}$ となるので、正規分布で近似できるとすれば $\color{red}{N\left(\dfrac{50+k}{2}, \dfrac{50+k}{4}\right)}$ に従う。（解答欄セ、ソ）

これより、ピーマン分類法によれば$$\small \begin{aligned} p_k &=P(25\leqq U_k\leqq 25+k) \\
&=P\left( 25-\dfrac{50+k}{2}\leqq U_k-\dfrac{50+k}{2}\leqq 25+k-\dfrac{50+k}{2} \right) \\
&=P\left( -\dfrac{k}{2}\leqq U_k-\dfrac{50+k}{2}\leqq \dfrac{k}{2} \right) \\
&=P\left( -\dfrac{k}{2}\cdot\dfrac{2}{\sqrt{50+k}} \leqq Y\leqq \dfrac{k}{2}\cdot\dfrac{2}{\sqrt{50+k}} \right) \\
&=\color{red}{P\left( -\dfrac{k}{\sqrt{50+k}} \leqq Y\leqq \dfrac{k}{\sqrt{50+k}} \right)} \end{aligned}$$と求められる。（解答欄タ）

問題文の誘導に従って $k>0$ の下で不等式$$k^2 \geqq 4(50+k)$$を解くと$$k \geqq 2+2\sqrt{51} \approx 2+2\cdot7.14=16.28$$を得る。故に $k_0=\color{red}{17}$ である。（解答欄チ、ツ）

（１）

$$\begin{aligned} a_3 &=1.01a_2 +p \\
&=1.01(1.01a_1+p) +p \\
&=\color{red}{1.01 \{ 1.01(10+p)+p \} +p} \end{aligned}$$ である。（解答欄ア）

$a_{n+1}=1.01a_n+p$ という漸化式が成立し、これは$$\color{red}{a_{n+1}+100p=1.01(a_n+100p)}$$と書き直すことができる。（解答欄イ～オ）

1年目のはじめに入金した$p$万円には $n-1$ 年分の利息が付くので $p\cdot{1.01}^{\color{red}{n-1}}$ となる。また、2年目のはじめに入金した$p$万円には $n-2$ 年分の利息が付くので $p\cdot{1.01}^{\color{red}{n-2}}$ となる。これを繰り返すと$$\small \begin{aligned} a_n
&=10\times 1.01^{n-1}+p\times1.01^{n-1}+p\times1.01^{n-2}+\cdots+p \\
&=\color{red}{10\times 1.01^{n-1}+p \displaystyle\sum_{k=1}^{n} 1.01^{k-1}} \end{aligned}$$と表せる。ここで、$$\begin{aligned} \displaystyle\sum_{k=1}^{n} 1.01^{k-1}&=\dfrac{1.01^n-1}{1.01-1} \\
&=\color{red}{100 (1.01^n-1)} \end{aligned}$$である。（解答欄カ～ケ）

（２）

10年目の終わりの預金額は $1.01 a_{10}$ となるから、$$\color{red}{1.01 a_{10}} \geqq 30$$が成り立てばよい。$a_n$の一般項の式に $n=10$ を代入して整理すると、$$p \geqq \color{red}{\dfrac{30-10\times 1.01^{10}}{101(1.01^{10}-1)}}$$となる。（解答欄コ～セ）

（１）

$\mathrm{M}$は線分$\mathrm{AB}$の中点なので、$$\overrightarrow{\mathrm{AM}} = \color{red}{\dfrac{1}{2}\overrightarrow{\mathrm{AB}} + \frac{1}{2}\overrightarrow{\mathrm{AC}}}$$と表せる。また、内積の定義より、$$\begin{cases} \overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AB}} = |\overrightarrow{\mathrm{AP}}| |\overrightarrow{\mathrm{AB}}| \cos\angle \mathrm{PAB} \\ \overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AC}} = |\overrightarrow{\mathrm{AP}}| |\overrightarrow{\mathrm{AC}}| \cos\angle \mathrm{PAC} \end{cases}$$であり、いま $\angle \mathrm{PAB}=\angle \mathrm{PAC}=\theta$ であるから、$$\dfrac{\overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AB}}}{|\overrightarrow{\mathrm{AP}}||\overrightarrow{\mathrm{AB}}|}=\dfrac{\overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AC}}}{|\overrightarrow{\mathrm{AP}}||\overrightarrow{\mathrm{AC}}|}=\color{red}{\cos\theta} \color{black}{\quad \cdots ①}$$が成り立つ。（解答欄ア～オ）

（２）

（１）の①式より、$$\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{\mathrm{AB}}=3\sqrt{2} \cdot 3 \cdot \dfrac{1}{\sqrt{2}}=\color{red}{9}$$である。また、$\overrightarrow{\mathrm{AP}}\perp\overrightarrow{\mathrm{PD}}$ のとき $\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{\mathrm{PD}}=0$ が成り立つから $\overrightarrow{\mathrm{AD}}=k\overrightarrow{\mathrm{AM}}$ と置くと、$$\overrightarrow{\mathrm{AP}}\cdot(\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{AP}})=0$$ $$\therefore k \,\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{\mathrm{AM}}-|\overrightarrow{\mathrm{AP}}|^2=0$$ $$\therefore \dfrac{1}{2}k \,\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{\mathrm{AB}}+\dfrac{1}{2}k \,\overrightarrow{\mathrm{AP}}\cdot\overrightarrow{\mathrm{AC}}-18=0$$ $$\therefore 9k-18=0$$ $$\therefore k=\color{red}{2}$$を得る。（解答欄カ、キ）

（３）（ⅰ）

$\overrightarrow{\mathrm{PA}} \perp \overrightarrow{\mathrm{PQ}}$ のとき、$$\overrightarrow{\mathrm{PA}} \cdot \overrightarrow{\mathrm{PQ}}= 0$$が成り立つ。いま、$\overrightarrow{\mathrm{AQ}}=2\overrightarrow{\mathrm{AM}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}$ であるから、$$\overrightarrow{\mathrm{PA}} \cdot (\overrightarrow{\mathrm{AQ}}-\overrightarrow{\mathrm{AP}})= 0$$ $$\therefore -\overrightarrow{\mathrm{AP}} \cdot (\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AP}})= 0$$ $$\therefore \color{red}{\overrightarrow{\mathrm{AP}} \cdot\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AP}} \cdot\overrightarrow{\mathrm{AC}}= \overrightarrow{\mathrm{AP}} \cdot \overrightarrow{\mathrm{AP}}}$$と式変形できる。これは$$|\overrightarrow{\mathrm{AP}}||\overrightarrow{\mathrm{AB}}|\cos \theta+|\overrightarrow{\mathrm{AP}}||\overrightarrow{\mathrm{AC}}|\cos \theta= |\overrightarrow{\mathrm{AP}}|^2$$と書き直せるから、両辺を$|\overrightarrow{\mathrm{AP}}|$で割って$$\color{red}{|\overrightarrow{\mathrm{AB}}|\cos \theta+|\overrightarrow{\mathrm{AC}}|\cos \theta= |\overrightarrow{\mathrm{AP}}|}$$を得る。（解答欄ク、ケ）

（３）（ⅱ）

$k \overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AB}} = \overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{AC}}$ のとき、$$k |\overrightarrow{\mathrm{AP}}||\overrightarrow{\mathrm{AB}}|\cos\theta =|\overrightarrow{\mathrm{AP}}||\overrightarrow{\mathrm{AC}}|\cos\theta$$ $$\therefore \color{red}{k |\overrightarrow{\mathrm{AB}}|=|\overrightarrow{\mathrm{AC}}|}$$となる。（解答欄コ：⓪）

$\overrightarrow{\mathrm{PA}}\perp \overrightarrow{\mathrm{PQ}}$ のとき前問の結果から$$|\overrightarrow{\mathrm{AB}}|\cos \theta+|\overrightarrow{\mathrm{AC}}|\cos \theta= |\overrightarrow{\mathrm{AP}}|$$が成り立つから、$$|\overrightarrow{\mathrm{AB}}|\cos \theta+k|\overrightarrow{\mathrm{AB}}|\cos \theta= |\overrightarrow{\mathrm{AP}}|$$ $$\therefore (1+k)|\overrightarrow{\mathrm{AB}}|\cos \theta= |\overrightarrow{\mathrm{AP}}|$$を得る。これは$$|\overrightarrow{\mathrm{AB^{\prime}}}|=\dfrac{1}{1+k}|\overrightarrow{\mathrm{AP}}|$$と書き換えられるから、点$\mathrm{B^{\prime}}$は線分$\mathrm{AP}$を$1:k$に内分する点であり、点$\mathrm{C^{\prime}}$は線分$\mathrm{AP}$を$k:1$に内分する点であることが分かる。（解答欄サ：④）

特に、$k=1$ のとき、点$\mathrm{B^{\prime}}$と$\mathrm{C^{\prime}}$はともに線分$\mathrm{AP}$の中点となり一致する。このとき、$\triangle \mathrm{PAB}$と$\triangle \mathrm{PAC}$はそれぞれ $\mathrm{BP}=\mathrm{BA}$、$\mathrm{CP}=\mathrm{CA}$ を満たす二等辺三角形となる。（なぜならば、点$\mathrm{B^{\prime}}$と$\mathrm{C^{\prime}}$は線分$\mathrm{AP}$の中点であり、かつ、それぞれ線分$\mathrm{AP}$に対する点$\mathrm{B}$および点$\mathrm{C}$の垂線の足だからである）

よって、$\overrightarrow{\mathrm{PA}}\perp \overrightarrow{\mathrm{PQ}}$ のとき、「シ」の解答群のうち②と③が必要性を満たすことが分かる。このうち「③ $\triangle \mathrm{PAB} \equiv \triangle \mathrm{PAC}$」のとき、$\angle \mathrm{APB}$が鈍角であるような三角形の場合、$\overrightarrow{\mathrm{PA}}\perp \overrightarrow{\mathrm{PQ}}$ は必ずしも成立しない。以上より、同値（必要十分）であるものは「② $\triangle \mathrm{PAB}$と$\triangle \mathrm{PAC}$がそれぞれ $\mathrm{BP}=\mathrm{BA}$、$\mathrm{CP}=\mathrm{CA}$ を満たす二等辺三角形」となる。（解答欄シ：②）