今回は3次元のベクトルの回転行列について簡単に紹介します。
3次元の回転行列の表式
ベクトル$\boldsymbol{r}$を単位ベクトル$\boldsymbol{n}$の周りに角$\theta$だけ回転させて新たに得られるベクトル$\boldsymbol{r}^{\prime}$は以下の「ロドリゲスの回転公式」(Rodrigues’ rotation formula)で与えられます。
ロドリゲスの回転公式
$$\small \color{green}{\boldsymbol{r}^{\prime}}\color{black}{=}\,\color{blue}{\boldsymbol{r}}\,\color{black}{ \cos \theta+(1-\cos \theta)(}\color{blue}{\boldsymbol{r}}\color{black}{ \cdot }\color{red}{\boldsymbol{n}}\color{black}{) }\color{red}{\boldsymbol{n}}\color{black}{+(}\color{red}{\boldsymbol{n}}\color{black}{ \times }\color{blue}{\boldsymbol{r}}\color{black}{) \sin \theta}$$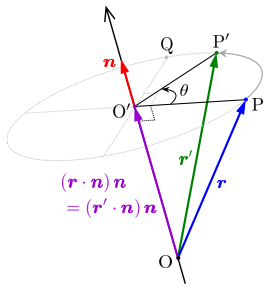
この公式は次のように導かれます。
図のように、回転軸方向の単位ベクトル $\boldsymbol{n}$ に垂直な回転面の中心を $\mathrm{O}^{\prime}$ とし、位置ベクトル $\boldsymbol{r}$、$\boldsymbol{r}^{\prime}$ の終点を $\mathrm{P}$、$\mathrm{P}^{\prime}$ とするとき、$$\overrightarrow{\mathrm{O}^{\prime} \mathrm{P}^{\prime}} = \overrightarrow{\mathrm{O}^{\prime} \mathrm{P}} \cos \theta + \overrightarrow{\mathrm{O}^{\prime} \mathrm{Q}} \sin \theta$$と表せます。ここで点 $\mathrm{Q}$ は回転面の円周上において $\mathrm{O}^{\prime}\mathrm{P}$ に垂直にとった点です。
$$\begin{align}\overrightarrow{\mathrm{OO}^{\prime}}&=(\boldsymbol{r} \cdot \boldsymbol{n}) \boldsymbol{n} \\ \overrightarrow{\mathrm{O}^{\prime} \mathrm{P}}&= \overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OO}^{\prime}} \\ &= \boldsymbol{r}-(\boldsymbol{r} \cdot \boldsymbol{n}) \boldsymbol{n} \\
\overrightarrow{\mathrm{O}^{\prime} \mathrm{Q}} &=\boldsymbol{n} \times \overrightarrow{\mathrm{O}^{\prime} \mathrm{P}} \\ &=\boldsymbol{n} \times\{\boldsymbol{r}-(\boldsymbol{r} \cdot \boldsymbol{n}) \boldsymbol{n}\} \\ &=\boldsymbol{n} \times \boldsymbol{r}\end{align}$$となるので、$$\small \begin{align} \boldsymbol{r}^{\prime} &= \overrightarrow{\mathrm{OP}^{\prime}} \\ &= \overrightarrow{\mathrm{OO}^{\prime}} + \overrightarrow{\mathrm{O}^{\prime} \mathrm{P}^{\prime}} \\ &=(\boldsymbol{r} \cdot \boldsymbol{n}) \boldsymbol{n}+\{\boldsymbol{r}-(\boldsymbol{r} \cdot \boldsymbol{n}) \boldsymbol{n}\} \cos \theta+(\boldsymbol{n} \times \boldsymbol{r}) \sin \theta \\ &=\boldsymbol{r} \cos \theta+(1-\cos \theta)(\boldsymbol{r} \cdot \boldsymbol{n}) \boldsymbol{n}+(\boldsymbol{n} \times \boldsymbol{r}) \sin \theta \end{align}$$となり、ロドリゲスの回転公式が得られます。
3次元の回転公式の成分表示
3次元の列ベクトル $\boldsymbol{n}=\left[\begin{array}{l}n_{1} \\ n_{2} \\ n_{3}\end{array}\right]$ と $\boldsymbol{r}=\left[\begin{array}{l}r_{1} \\ r_{2} \\ r_{3}\end{array}\right]$ の外積は$$\begin{align} \boldsymbol{n} \times \boldsymbol{r} &= \left[\begin{array}{cc}n_{2} r_{3}-n_{3} r_{2} \\ n_{3} r_{1}-n_{1} r_{3} \\ n_{1} r_{2}-n_{2} r_{1}\end{array}\right] \\ &= \left[\begin{array}{ccc}0 & -n_{3} & n_{2} \\ n_{3} & 0 & -n_{1} \\ -n_{2} & n_{1} & 0 \end{array}\right]\left[\begin{array}{l}r_{1} \\ r_{2} \\ r_{3}\end{array}\right] \\ &= A \boldsymbol{r} \end{align}$$と表せるので、外積は表現行列 $A=\left[\begin{array}{ccc}0 & -n_{3} & n_{2} \\ n_{3} & 0 & -n_{1} \\ -n_{2} & n_{1} & 0 \end{array}\right]$ を用いて1次変換として表すことができます。
いま、$$\boldsymbol{n} \times \boldsymbol{r} = \left[\begin{array}{ccc}0 & -n_{3} & n_{2} \\ n_{3} & 0 & -n_{1} \\ -n_{2} & n_{1} & 0 \end{array}\right]\left[\begin{array}{l}r_{1} \\ r_{2} \\ r_{3}\end{array}\right] = A \boldsymbol{r}$$であり、$$\begin{align}
(\boldsymbol{r} \cdot \boldsymbol{n}) \boldsymbol{n} &= \boldsymbol{n}^{t} \boldsymbol{n} \boldsymbol{r} \\ &= \left[\begin{array}{c}
n_{1} \\
n_{2} \\
n_{3}
\end{array}\right]\left[\begin{array}{llll}
n_{1} & n_{2} & n_{3}
\end{array}\right] \boldsymbol{r} \\
&= \left[\begin{array}{ccc}
n_{1}^{2} & n_{1} n_{2} & n_{1} n_{3} \\
n_{1} n_{2} & n_{2}^{2} & n_{2} n_{3} \\
n_{1} n_{3} & n_{2} n_{3} & n_{3}^{2}
\end{array}\right] \boldsymbol{r}
\end{align}$$であり、$$\small \boldsymbol{r}^{\prime} = \left\{\cos \theta \, I+(1-\cos \theta) \boldsymbol{n}^{t} \boldsymbol{n}+\sin \theta\,A\right\} \boldsymbol{r}$$と表されるので、回転行列$R_n(\theta)$は$$\scriptsize \begin{align}
& \quad R_n(\theta) \\ &= \cos \theta \,I+(1-\cos \theta) \boldsymbol{n}^{t} \boldsymbol{n}+\sin \theta\,A \\
&=\cos \theta\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]+(1-\cos \theta)\left[\begin{array}{ccc}
n_{1}^{2} & n_{1} n_{2} & n_{1} n_{3} \\
n_{1} n_{2} & n_{2}^{2} & n_{2} n_{3} \\
n_{1} n_{3} & n_{2} n_{3} & n_{3}^{2}
\end{array}\right]+\sin \theta\left[\begin{array}{ccc}
0 & -n_{3} & n_{2} \\
n_{3} & 0 & -n_{1} \\
-n_{2} & n_{1} & 0
\end{array}\right] \\
& = \left[\begin{array}{ccc}
n_{1}^{2}(1-\cos \theta)+\cos \theta & n_{1} n_{2}(1-\cos \theta)-n_{3} \sin \theta & n_{1} n_{3}(1-\cos \theta)+n_{2} \sin \theta \\
n_{1} n_{2}(1-\cos \theta)+n_{3} \sin \theta & n_{2}^{2}(1-\cos \theta)+\cos \theta & n_{2} n_{3}(1-\cos \theta)-n_{1} \sin \theta \\
n_{1} n_{3}(1-\cos \theta)-n_{2} \sin \theta & n_{2} n_{3}(1-\cos \theta)+n_{1} \sin \theta & n_{3}^{2}(1-\cos \theta)+\cos \theta
\end{array}\right]
\end{align}$$と成分表示されます($I$は単位行列です)。
※単位ベクトル$\boldsymbol{n}$の定義上、ベクトルの$z$成分を$0$にしても$R_n(\theta)$は平面上の回転を表す行列にはなりません。
回転行列の使用例
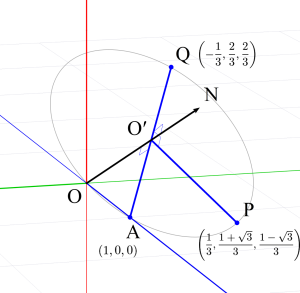
この回転行列を使って少し遊んでみましょう。ベクトル$\small \left(\dfrac{1}{\sqrt{3}},\dfrac{1}{\sqrt{3}},\dfrac{1}{\sqrt{3}}\right)$方向に点$(1,0,0)$を$90^{\circ}$だけ回転した点を求めてみます。$$\scriptsize \begin{align} & \quad R_n(90^{\circ}) \\ &= \left[\begin{array}{ccc}
\dfrac{1}{3}(1-\cos 90^{\circ})+\cos 90^{\circ} & \dfrac{1}{3}(1-\cos 90^{\circ})-\dfrac{1}{\sqrt{3}} \sin 90^{\circ} & \dfrac{1}{3}(1-\cos 90^{\circ})+\dfrac{1}{\sqrt{3}} \sin 90^{\circ} \\
\dfrac{1}{3}(1-\cos 90^{\circ})+\dfrac{1}{\sqrt{3}} \sin 90^{\circ} & \dfrac{1}{3}(1-\cos 90^{\circ})+\cos 90^{\circ} & \dfrac{1}{3}(1-\cos 90^{\circ})-\dfrac{1}{\sqrt{3}} \sin 90^{\circ} \\
\dfrac{1}{3}(1-\cos 90^{\circ})-\dfrac{1}{\sqrt{3}} \sin 90^{\circ} & \dfrac{1}{3}(1-\cos 90^{\circ})+\dfrac{1}{\sqrt{3}} \sin 90^{\circ} & \dfrac{1}{3}(1-\cos 90^{\circ})+\cos 90^{\circ}
\end{array}\right] \\ &= \left[\begin{array}{ccc}
\dfrac{1}{3}(1-0)+0 & \dfrac{1}{3}(1-0)-\dfrac{1}{\sqrt{3}} & \dfrac{1}{3}(1-0)+\dfrac{1}{\sqrt{3}} \\
\dfrac{1}{3}(1-0)+\dfrac{1}{\sqrt{3}} & \dfrac{1}{3}(1-0)+0 & \dfrac{1}{3}(1-0)-\dfrac{1}{\sqrt{3}} \\
\dfrac{1}{3}(1-0)-\dfrac{1}{\sqrt{3}} & \dfrac{1}{3}(1-0)+\dfrac{1}{\sqrt{3}} & \dfrac{1}{3}(1-0)+0
\end{array}\right] \\ &= \left[\begin{array}{ccc}
\dfrac{1}{3} & \dfrac{1-\sqrt{3}}{3} & \dfrac{1+\sqrt{3}}{3} \\
\dfrac{1+\sqrt{3}}{3} & \dfrac{1}{3} & \dfrac{1-\sqrt{3}}{3} \\
\dfrac{1-\sqrt{3}}{3} & \dfrac{1+\sqrt{3}}{3} & \dfrac{1}{3}
\end{array}\right] \end{align}$$となるから、$$\small \begin{align} R_n(90^{\circ})\left[\begin{array}{c}
1 \\
0 \\
0
\end{array}\right] &= \left[\begin{array}{ccc}
\dfrac{1}{3} \\
\dfrac{1+\sqrt{3}}{3} \\
\dfrac{1-\sqrt{3}}{3}
\end{array}\right] \end{align}$$より、求める点は$\small \left(\dfrac{1}{3},\dfrac{1+\sqrt{3}}{3},\dfrac{1-\sqrt{3}}{3}\right)$となります。これに対してさらに$R_n(90^{\circ})$を適用すると、$$\small \begin{align} R_n(90^{\circ})\left[\begin{array}{ccc}
\dfrac{1}{3} \\
\dfrac{1+\sqrt{3}}{3} \\
\dfrac{1-\sqrt{3}}{3}
\end{array}\right] &= \left[\begin{array}{ccc}
-\dfrac{1}{3} \\
\dfrac{2}{3} \\
\dfrac{2}{3}
\end{array}\right] \end{align}$$となります。
このとき、$\boldsymbol{r}=\overrightarrow{\mathrm{OA}}$、$\boldsymbol{r}^{\prime}=\overrightarrow{\mathrm{OP}}$、$\boldsymbol{r}^{\prime\prime}=\overrightarrow{\mathrm{OQ}}$と置くと、各点の位置関係は上の図のようになっており、ちゃんと $\overrightarrow{\mathrm{ON}} \perp \overrightarrow{\mathrm{AQ}}$ や $\overrightarrow{\mathrm{O^{\prime}P}} \perp \overrightarrow{\mathrm{O^{\prime}A}}$ などを満たしています。
以上の内容は工学系の分野くらいでしか使われない知識ですが、なかなか面白い結果だと思います。ある軸を中心に直角になるようにベクトルを回すなどするときは空間のベクトル方程式でも求められます。ゲームなどで三次元の物体を回転させる操作には「四元数」(クォータニオン:Quaternion)が用いられます。因みにこれは「しげんすう」と読みます。