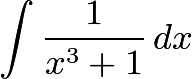第2次偏導関数を成分とする「ヘッセ行列」の情報を使えば多変数関数の極値判定が可能です。今回は多変数関数の停留点に対する極値判定の方法について解説します。
「テイラー展開」の分かりやすい解説
この記事では「テイラー展開」という数学的操作について例を交えて分かりやすく解説します。
べき乗/階乗の無限級数の性質③
べき乗が階乗で割られた形の無限級数をまとめます。これまでに扱ってきた数列群を、母関数を用いて高い視点から眺めてみます。
べき乗/階乗の無限級数の性質②
前回に引き続き、べき乗が階乗で割られた形の数列からなる無限級数について考察してみます。
べき乗/階乗の無限級数の性質①
べき乗が階乗で割られた形の数列からなる無限級数に関する面白い性質を紹介します。
合成関数の漸近展開を簡単に求める方法
複雑な関数の漸近展開を求める際、いちいち微分していると計算ミスを誘発する危険性があります。本稿では合成関数の漸近展開を簡単に求める方法を紹介します。
多項式のラプラス変換の一般化
電磁気的な現象や化学反応の速度論を解析する場合、(連立)微分方程式を解く必要が生じる。この際に有用な数学的な処理にラプラス変換がある。本稿では一般の多項式に対するラプラス変換について述べる。
【数Ⅲ】1/(x^3-1)の微分積分
昨日の続きです。今回は関数 1/(x^3-1) の導関数と不定積分の導出ついて解説します。関数 x/(x^3-1) や x^2/(x^3-1) についても触れます。
【数Ⅲ】1/(x^3+1)の微分積分
本稿では関数 1/(x^3+1) の導関数と不定積分の導出ついて解説します。関数 x/(x^3+1) についても触れます。
【大学微積】基本的な整級数展開一覧
大学範囲の微積分野の備忘録として、今回は基本的な関数の整級数展開(マクローリン展開)を一覧にしました!