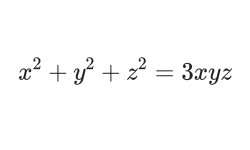今年の東大理系数学の整数問題は論証題でした。
【2025年】共通テスト数学ⅠA第1問
2025年の共通テスト数学ⅠAの第1問を解説します。
3次式が素数になる条件(2024年東京大学前期理系数学第6問)
今年も2次試験のシーズンがやってきましたね。今日行われた入試問題の中から、東大理系数学で出題された整数問題を紹介します。
k^5*x-2^5*y=1の整数解(2022年共テ数ⅠA第4問)
2022年共通テスト数学ⅠAの整数問題で出題された1次不定方程式の係数は巨大で、規則性を見つけないと容易には解けないよう設計されていました。本稿ではこの問題で出題された方程式の整数解について考察してみます。
整式の因数分解(2006年京都大学後期理系数学第1問)
一昔前の京大後期で出題された整式に関する証明問題を紹介します。
一次不定方程式が解をもつ条件(2021年東北大学後期共通数学第1問)
今年の東北大学の後期では一次不定方程式に関する一般的な問題が出題されました。
4次方程式の解の公式(Ferrariの解法)
本稿では4次方程式の解の公式、いわゆる「Ferrariの公式」を導出します!
マルコフ数を構成する方法
今回は整数論の分野から「マルコフ数」の話題を取り上げてみます。
【数学夏祭り】第7’問(関数方程式)について【2020年夏】
先週まで2週間にわたって開催された「数学夏祭り」第7問の代替問題(第7’問)について解説・考察してみました。
(2020/09/15追記)
この記事が数学夏祭り問7´の解説賞に選ばれました!(当サイトの解説賞の受賞は問4に続いて2回目です)
#数学夏祭り 問7代替問題の解説賞!@science_log
【数学夏祭り】第7’問(関数方程式)について【2020年夏】 | 理系のための備忘録 https://t.co/sMjSofGHsS
おめでとうございます!
キャンペーンプライズをお送りします。これで数学夏祭りの表彰発表はおしまい!#数学夏祭り解説 pic.twitter.com/gvMahgipZk
— 数学夏祭り@もう秋かな (@mathmatsuri) September 15, 2020
3次方程式を経由する連立方程式(近畿大学2018年(医)数学第3問)
2018年の近畿大学医学部の入試数学から代数の問題を紹介します。誘導設問が丁寧なので是非とも完答したい問題です。