大学受験の勉強をするようになると、そして社会に一度出てしまうとなかなか純粋な幾何・図形に触れる機会が無くなるというものです。そこで今回は「相似」をテーマにちょっとした頭の体操を用意しました。
問題は適当に選んでいます。気楽に取り組んでみて下さい。
※「このサイトを離れますか?」というポップアップが出ますが、GeoGebraの仕様なので無視して構いません。
高校入試から①
2014年の京都府の公立高校入試で出題された図形問題です。
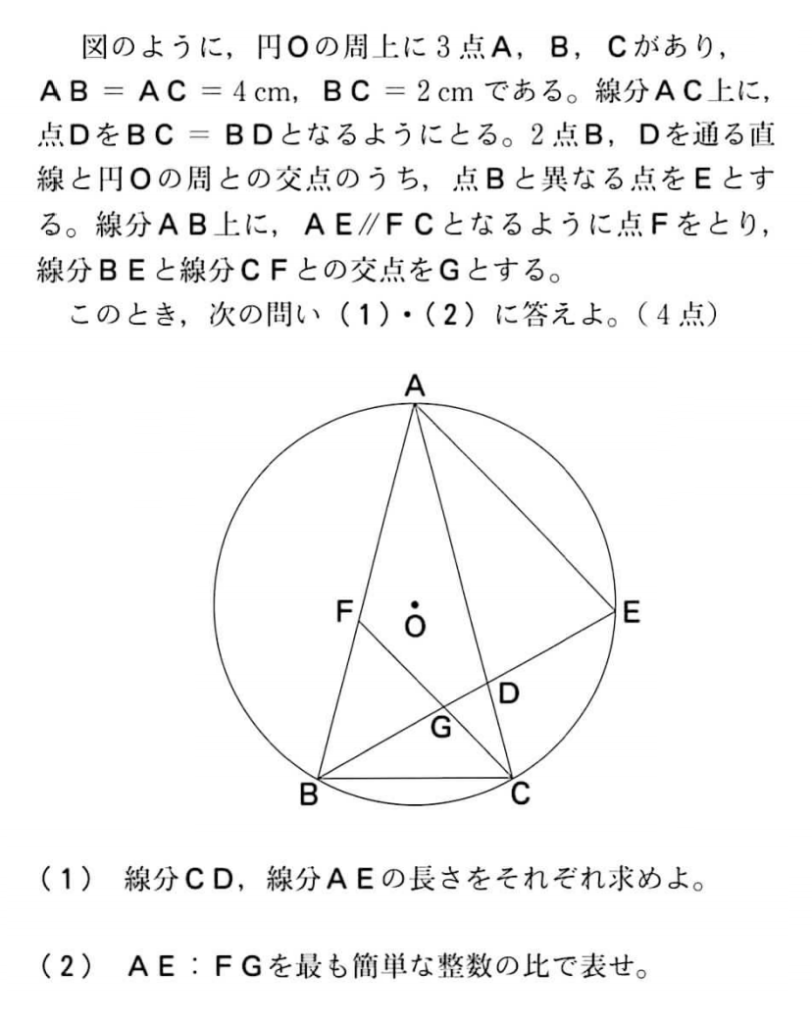 (出典:京都府公立高校入試2014年)
(出典:京都府公立高校入試2014年)
※問題文の表現を一部変更
» 解答の流れ
(解答の流れ)
底角が等しい二等辺三角形であることから $\triangle \mathrm{ABC} \sim \triangle \mathrm{BCD}$ であり、$$\mathrm{CD}=1\,[\text{cm}]$$を得ます。また、対頂角について $\angle \mathrm{CDB}=\angle \mathrm{ADE}$、円周角について $\angle \mathrm{DBC}=\angle \mathrm{EAD}$ から、$\triangle \mathrm{BCD} \sim \triangle \mathrm{ADE}$ であり、$\triangle \mathrm{ADE}$は二等辺三角形であることが分かります。これより、$$\mathrm{AE}=\mathrm{AD}=\mathrm{AC}-\mathrm{CD}=3\,[\text{cm}]$$を得ます。
(2)については、相似比から $\mathrm{DE}=1.5\,[\text{cm}]$ と分かるので、$$\mathrm{BE}=\mathrm{BD}+\mathrm{DE}=3.5\,[\text{cm}]$$と求められます。また、$\mathrm{AE} \,/\!/\, \mathrm{CG}$ より $\triangle \mathrm{ADE} \sim \triangle \mathrm{CDG}$ であるから相似比より $\mathrm{DG}=0.5\,[\text{cm}]$ と求められ、$\mathrm{AE} \,/\!/\, \mathrm{GF}$ より $\triangle \mathrm{ABE} \sim \triangle \mathrm{FBG}$ であるから、$$\begin{align} \mathrm{AE}:\mathrm{FG} &=\mathrm{BE}:\mathrm{BG} \\ &=3.5:1.5 \\ &=7:3 \end{align}$$となります。シンプルな問題でしたね。
» 閉じる
高校入試から②
2015年の神奈川県の公立高校入試で出題された図形の証明問題です。
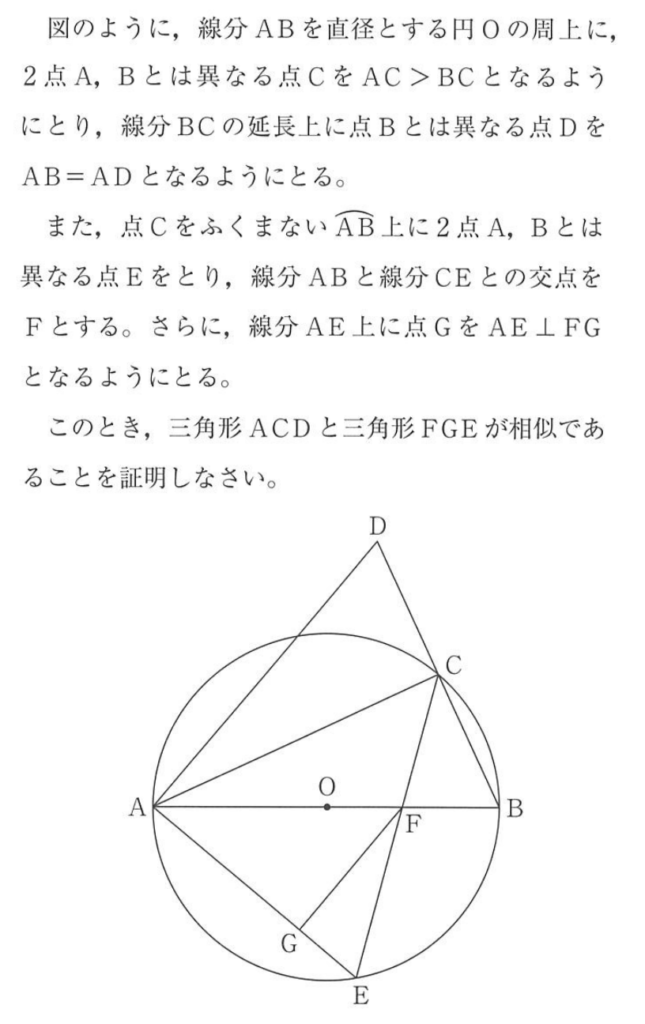 (出典:神奈川県公立高校入試2015年)
(出典:神奈川県公立高校入試2015年)
※問題文の表現を一部変更
これだけでは簡単すぎるので、以下の設問を追加します。
(2)$\mathrm{AD} \,/\!/\, \mathrm{FG}$ のとき $\mathrm{CA}=\mathrm{CE}$ であることを証明しなさい。
(3)$\mathrm{CA}=\mathrm{CE}$ のとき $\mathrm{AD} \,/\!/\, \mathrm{FG}$ であることを証明しなさい。
これでそれなりの難度になると思います。補助線を上手く使いましょう。
» 解答の流れ
(解答の流れ)
$\mathrm{AB}=\mathrm{AD}$ より$\triangle \mathrm{ABD}$は二等辺三角形であるから $\angle \mathrm{ABC} = \angle \mathrm{ADC}$ であり、$\mathrm{AB}$が円$\mathrm{O}$の直径だから $\angle \mathrm{BCA} = 90^{\circ}$ なので $\angle \mathrm{ACD} = 90^{\circ}$ です。$\mathrm{AE}\perp\mathrm{FG}$ より $\angle \mathrm{FGE} = 90^{\circ}$ であるので、直角三角形の直角以外の1つの角度が等しいことから、$$\triangle \mathrm{ACD} \sim \triangle \mathrm{FGE}$$が導かれます。ここまでは詰まらずに辿り着けるはずです。
(2)は以下のように示せます。
$\mathrm{AD} \,/\!/\, \mathrm{FG}$ より同位角の関係から$$\angle \mathrm{DAE}=\angle \mathrm{FGE}= 90^{\circ}$$となります。前問より $\triangle \mathrm{ACD} \sim \triangle \mathrm{FGE}$ なので$$\angle \mathrm{DAC} = \angle \mathrm{EFG} \quad \cdots ①$$が成り立ちます。
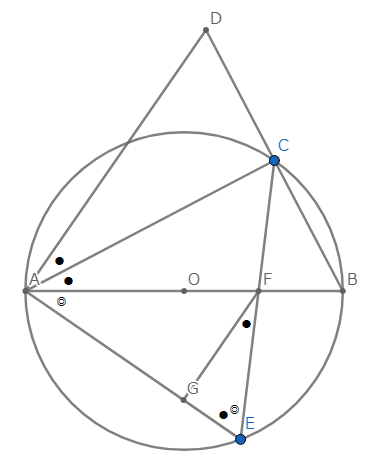
ここで、$\angle \mathrm{CAE}=90^{\circ}-\angle \mathrm{DAC}$ であり、$\triangle \mathrm{FGE}$は直角三角形なので補角の関係から $\angle \mathrm{CEA}=90^{\circ}-\angle \mathrm{EFG}$ です。よって$①$より、$$\angle \mathrm{CAE}=\angle \mathrm{CEA}$$が成り立つので、$\triangle \mathrm{CAE}$は底角が等しい三角形となることから二等辺三角形であり、$$\mathrm{CA}=\mathrm{CE}$$が従います。
なお、証明には必要ありませんが、$\triangle \mathrm{ABD}$は二等辺三角形であり、$\angle \mathrm{ACB}=90^{\circ}$であるから$\mathrm{AC}$は$\angle \mathrm{BAD}$の二等分線となるので $\angle \mathrm{BAC} = \angle \mathrm{DAC}$ が成り立っています。
(3)は下図のように$\mathrm{C}$から$\mathrm{AE}$に対して垂線$\mathrm{CH}$を引いて、同位角、錯角の関係を利用します。
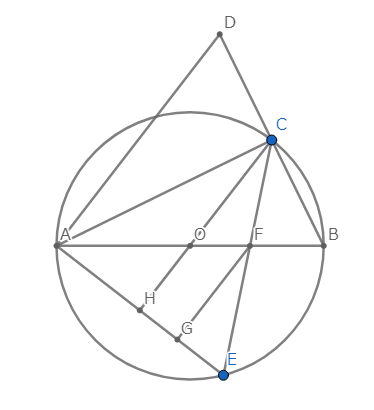
$\angle \mathrm{CHE}$と$\angle \mathrm{FGE}$はともに$90^{\circ}$であり、同位角の関係から、$$\mathrm{CH} \,/\!/\, \mathrm{FG} \quad \cdots ①$$であることが従います。$①$より同位角の関係から$$\angle \mathrm{ECH}=\angle \mathrm{EFG} \quad \cdots ②$$が成り立ちます。
いま、$\mathrm{CA}=\mathrm{CE}$ なので$\triangle \mathrm{ACE}$は二等辺三角形であり、$\mathrm{CH}$は二等辺三角形の頂点$\mathrm{C}$から底辺に対して下ろした垂線なので、頂角$\angle \mathrm{ACE}$の二等分線でもあります。これより$$\angle \mathrm{ECH}=\angle \mathrm{ACH} \quad \cdots ③$$が成り立ちます。
ここで、$\triangle \mathrm{ACD} \sim \triangle \mathrm{FGE}$ なので$$\angle \mathrm{DAC}=\angle \mathrm{EFG} \quad \cdots ④$$が成り立っています。したがって$②$~$④$から$$\angle \mathrm{DAC}=\angle \mathrm{ACH}$$が成り立ちます。この2つの角は錯角の関係にあるので、ここから $\mathrm{AD} \,/\!/\, \mathrm{FG}$ が導かれます。
以上より、$\mathrm{AD} \,/\!/\, \mathrm{FG}$ は $\mathrm{CA}=\mathrm{CE}$ の必要十分条件であることが示されました。以下にGeoGebraにより描画した図を共有します。点$\mathrm{C}$、$\mathrm{E}$を動かせるようにしてあるので遊んでみて下さい。
点$\mathrm{I}$は直線$\mathrm{EC}$と$\mathrm{AD}$の交点です。「$\mathrm{EC}=\mathrm{CI}$ のとき $\mathrm{AD}\perp\mathrm{AE}$ を示せ」(またはその逆)などの証明問題も面白そうですね。
» 閉じる
図形問題というのは、発想力と視野の広さを試すのに適していると同時に、数学の純粋な面白さを思い出させてくれる存在です。別に図形問題が苦手だからといって地頭が悪い証拠にはなりません。多くの場合、幾何は慣れがモノを言います。色々な問題に触れたり、別解を沢山与えたり、自作問題を解いてみたりして、少しずつ「図形を見る目」を養っていけば良いでしょう。何事も楽しんで取り組むことが大切です。
