「相似」シリーズ第3弾。今回は数学コンテストの問題を取り上げます。
※「このサイトを離れますか?」というポップアップが出ますが、GeoGebraの仕様なので無視して構いません。
数学コンテストでは微分積分などの解析学は出題されず、代数や数論(整数分野)、幾何(平面図形)、組み合わせ論やグラフ理論などの離散数学という、主に3分野から選りすぐりの問題が数問出題されます。大学入試とはまた違った趣の難問が揃っており、頭を使ってじっくり考えるのに丁度良い問題ばかりです。
日本で有名な数学コンテストと言えば、やはり「数学オリンピック」でしょう。「日本数学オリンピック」は “JMO” と呼ばれる国内の数学コンテストの最高峰であり、毎年多くの高校・中学生が参加しています(中には小学生の参加者もいます)。世界で最もレベルの高い数学コンテストは言わずと知れた「国際数学オリンピック」通称 “IMO” で、世界トップレベルの参加者が競い合うだけあって、どの年も難問揃いです。
IMOのレベルとはいかないまでも、国際的な数学コンテストでは高難度の図形問題が取材されています。今回はその一部をちょっとだけ紹介してみます。
2011 JJMO 予選 Q4
まずは初級編。JJMO は「日本ジュニア数学オリンピック」の略称です。
三角形$\mathrm{ABC}$の辺$\mathrm{AB}$上に点$\mathrm{D}$、辺$\mathrm{AC}$上に点$\mathrm{E}$を、直線$\mathrm{DE}$と直線$\mathrm{BC}$が平行になるようにとる。線分$\mathrm{BD}$の中点を$\mathrm{M}$とし、線分$\mathrm{CE}$の中点を$\mathrm{N}$とする。四角形$\mathrm{DMNE}$の面積が$1$、四角形$\mathrm{MBCN}$の面積が$2$であるとき、三角形$\mathrm{ADE}$の面積を求めよ。
(2011年 日本ジュニア数学オリンピック予選 第4問)
図に起こすと次のようになります。
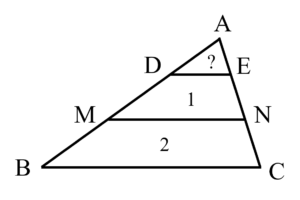
» 解答の流れ
(解答の流れ)
三角形$\mathrm{ABC}$と合同な三角形を付け足して平行四辺形にして考える方法などもありますが、単純に面積比を考えていくストレートな方法が分かりやすいと思います。
$\mathrm{AD}:\mathrm{DM}:\mathrm{MB}=x:1:1$、$\triangle \mathrm{ADE}=S$ と置きます。このとき$$\small \begin{cases} \triangle \mathrm{ADE}:\triangle \mathrm{AMN}=S:1+S=x^2:(x+1)^2 \\ \triangle \mathrm{ADE}:\triangle \mathrm{ABC}=S:3+S=x^2:(x+2)^2 \end{cases}$$となるので、$$\begin{cases} (1+S)x^2=S(x+1)^2 \quad \cdots ① \\ (3+S)x^2=S(x+2)^2 \quad \cdots ② \end{cases}$$を得ます。$② \div ①$ より、$$\dfrac{3+S}{1+S}=\dfrac{(x+2)^2}{(x+1)^2}$$ $$\therefore 1+\dfrac{2}{1+S}=\dfrac{(x+2)^2}{(x+1)^2}$$ $$\therefore \dfrac{1+S}{2}=\dfrac{1}{\dfrac{(x+2)^2}{(x+1)^2}-1}$$ $$\therefore S=\dfrac{2}{\dfrac{(x+2)^2}{(x+1)^2}-1}-1 \quad \cdots ③$$と表せます。$①$に$③$を代入して$$\small \dfrac{2x^2}{\dfrac{(x+2)^2}{(x+1)^2}-1}=\left\{\dfrac{2}{\dfrac{(x+2)^2}{(x+1)^2}-1}-1\right\}(x+1)^2$$ $$\small \therefore 2x^2=\left\{2-\left(\dfrac{(x+2)^2}{(x+1)^2}-1\right)\right\}(x+1)^2$$ $$\therefore 2x^2=3(x+1)^2-(x+2)^2$$ $$\therefore 0=-1+2x$$ $$\therefore x=\dfrac{1}{2}$$を得ます。2次式が出てきますが2次の項は打ち消し合って結局1次の方程式になるので中学生でも解けます。これを$①$に代入して$$\dfrac{1}{4}(1+S)=\dfrac{9}{4}S$$ $$\therefore S=\color{red}{\dfrac{1}{8}}$$と求められます。
「面積比=相似比の2乗」というのは常識ですね。式が沢山書いてありますが、変に展開したりせずカタマリのまま計算していけば、見た目の割に計算が簡単です。
» 閉じる
1993 APMO Q1

日本語に直すと以下のようになります。
$\mathrm{ABCD}$は全ての辺の長さが等しく $\angle \mathrm{ABC}=60^{\circ}$ であるような四角形である。$\ell$ は$\mathrm{D}$を通りこの四角形と($\mathrm{D}$以外では)交わらない直線である。直線$\mathrm{AB}$、$\mathrm{BC}$と $\ell$ との交点をそれぞれ$\mathrm{E}$と$\mathrm{F}$する。直線$\mathrm{CE}$と$\mathrm{AF}$の交点を$\mathrm{M}$とする。このとき $\mathrm{CA}^2=\mathrm{CM} \times \mathrm{CE}$ を示せ。
さて、どこに相似な図形があるか見えますか?
» 解答の流れ
(解答の流れ)
問題文の条件を図に起こすと以下のようになります。長さ$\mathrm{AC}$と$\mathrm{CM}\times\mathrm{CE}$ の値を表示しています。点$\mathrm{A}$と$\mathrm{P}$は自由に動かせるようにしているので、色々動かしても $\mathrm{CA}^2=\mathrm{CM}\times\mathrm{CE}$ が成り立っていることを確かめて下さい。
四角形$\mathrm{ABCD}$は $\angle \mathrm{ABC}=60^{\circ}$ の菱形です。$\mathrm{AD} /\!/ \mathrm{BC}$ より $\angle \mathrm{EAD}=\angle \mathrm{ABC}=\angle \mathrm{DCF}$、$\mathrm{AB} /\!/ \mathrm{CD}$ より $\angle \mathrm{AED}=\angle \mathrm{CDF}$ が成り立つから、$$\triangle \mathrm{ADE} \sim \triangle \mathrm{CFD}$$です。これより$$\mathrm{AE}:\mathrm{AD}=\mathrm{CD}:\mathrm{CF} \ \cdots ①$$となりますが、四角形$\mathrm{ABCD}$が $\angle \mathrm{ABC}=60^{\circ}$ の菱形であることから、$$\mathrm{AD}=\mathrm{AC}=\mathrm{CD} \ \cdots ②$$なので、$①$と$②$より$$\mathrm{AE}:\mathrm{AC}=\mathrm{AC}:\mathrm{CF}$$が成り立ちます。これと $\angle \mathrm{CAE}=\angle \mathrm{FCA}=120^{\circ}$ から、$$\triangle \mathrm{ACE} \sim \triangle \mathrm{CFA}$$と分かります。故に $\angle \mathrm{AEC}=\angle \mathrm{CAF}$ であり、$\angle \mathrm{ACE}$と$\angle \mathrm{MCA}$は共通であることから、$$\triangle \mathrm{ACE} \sim \triangle \mathrm{MCA}$$です。したがって辺の相似比について$$\mathrm{CE}:\mathrm{CA}=\mathrm{CA}:\mathrm{CM}$$が成り立つので、$$\mathrm{CA}^2=\mathrm{CM} \times \mathrm{CE}$$の成立が示されます。
$\mathrm{ABCD}$が正三角形2個からなる菱形、というのが本問のポイントでした。
» 閉じる
2015 Baltic Way Q15
In triangle $ABC$, the interior and exterior angle bisectors of $ \angle BAC$ intersect the line $BC$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $AD$ with the circumcircle of the triangle $ABC$. Let $O$ be the circumcentre of the triangle $ABC$ and let $D’$ be the reflection of $D$ in $O$. Prove that $\angle D’FE=90$.
(2015年 Baltic Way 第15問)
日本語に直すと以下のようになります。
三角形$\mathrm{ABC}$において、$\angle \mathrm{BAC}$の内角および外角の二等分線と直線$BC$との交点をそれぞれ$D$、$E$とする。$F$を直線$AD$と三角形$\mathrm{ABC}$の外接円との($A$でない方の)交点とする。$O$を三角形$\mathrm{ABC}$の外接円の中心とし、点$O$に関する点$D$の鏡像を$D’$とする。このとき $\angle D’FE=90$ を示せ。
様々な解法が考えられる良い問題です。内角・外角の二等分線はなかなか入試に登場しないので新鮮かもしれません。是非一度は自力で解いてみて下さい。
Baltic Way は名前の通りバルト海に面する「バルト三国」を中心とした国々が参加する国際数学コンテストで、1990年から毎年開催されています。各参加国は5人の高校生チームを編成し、4時間半で20題の難問を協力して解き、合計点を競うという形式です。代数、組み合わせ論、幾何、数論からそれぞれ5題ずつ出題されるのが通例で、個人の能力だけでなく、各メンバーの得意分野に合わせた戦略も重要になるコンテストです。
» 解答の流れ
(解答の流れ)
直線$EA$と$\triangle ABC$の外接円$O$との$A$でないもう一つの交点を$G$とすると、$AD$と$AE$がそれぞれ内角と外角の二等分線であることから$$\angle DAE=\angle DAG=90^{\circ}$$が成り立ちます。これより $\angle FAG=90^{\circ}$ となるので、線分$FG$は外接円$O$の直径と分かります。ここで$BC$と$FG$の交点を$M$とし、直線$EF$と$\triangle ABC$の外接円$O$との$F$でないもう一つの交点を$H$とします。
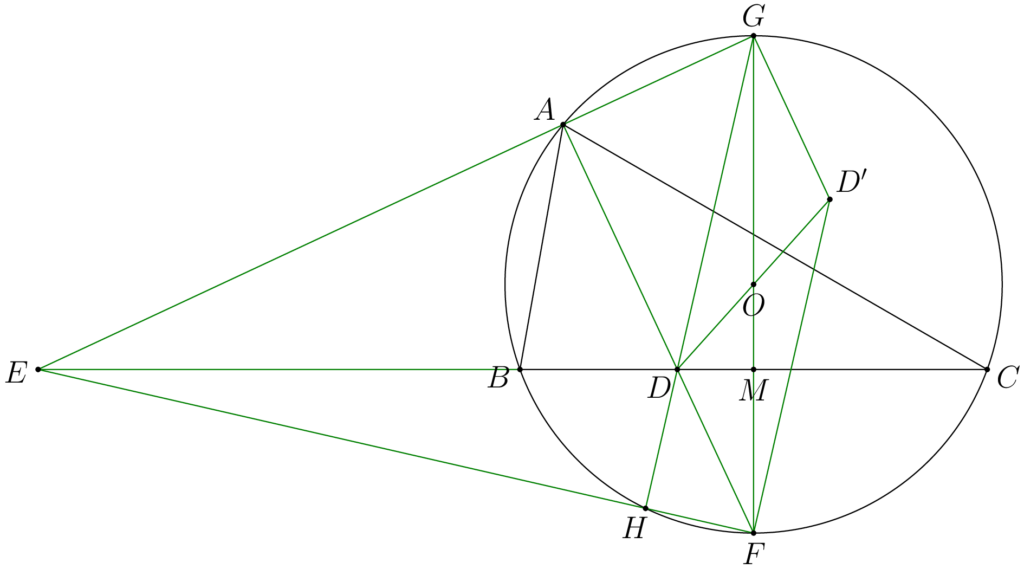
$D$と$D’$、および$F$と$G$はそれぞれ点$O$に関する鏡像なので、$OD=OD’$、$FD=GD’$、$FD’=GD$ が成り立ち、$OF=OG$ と合わせると $\triangle ODF \equiv \triangle OD’G$ および $\triangle OD’F \equiv \triangle ODG$ が導かれます。よって、$\angle OFD = \angle OGD’$ と $\angle OGD = \angle OFD’$ が従うので、$$\angle DFD’ = \angle D’GD \quad \cdots ①$$が成り立ちます。
また、錯角が等しいので $FD /\!/ GD’$ であり、$AD \perp AE$ より $D’G \perp AG$、すなわち、$$\angle AGD’ = 90^{\circ} \quad \cdots ②$$が分かります。
ここで、円周角の定理より $\angle HFA = \angle AGH$ が成り立つから、$①$、$②$より$$\angle DFD’+\angle HFA = \angle D’GD +\angle AGH = 90^{\circ}$$を得るので、$\angle EFD’=90^{\circ}$ が示されます。
$EA$を延長して点$G$を持ち出すと議論しやすくなります。相似に固執し過ぎると却って遠回りしかねない問題でした。
» 閉じる

余談ですが、英語では「相似図形」を “similar figure(s)” と呼びます。”math olympiad geometry” などで検索すると色々な問題が見つけられます。受験勉強に飽きたら気分転換に適当な問題を見つけて解いてみると良いかもしれません。
昔は時々どこかの数学コンテストの改題が日本の高校入試や大学入試に出ていたりしたのですが、最近は典型題や解析分野からの出題が増えており、そういう問題を見かけなくなった気がします。