幾つかの正五角形の頂点を結んでできる線分の長さに関する雑談です。
下図は3つの正五角形を並べた図です。図中の色を付けた線分について、図に示したような等式が成り立つことが知られています。
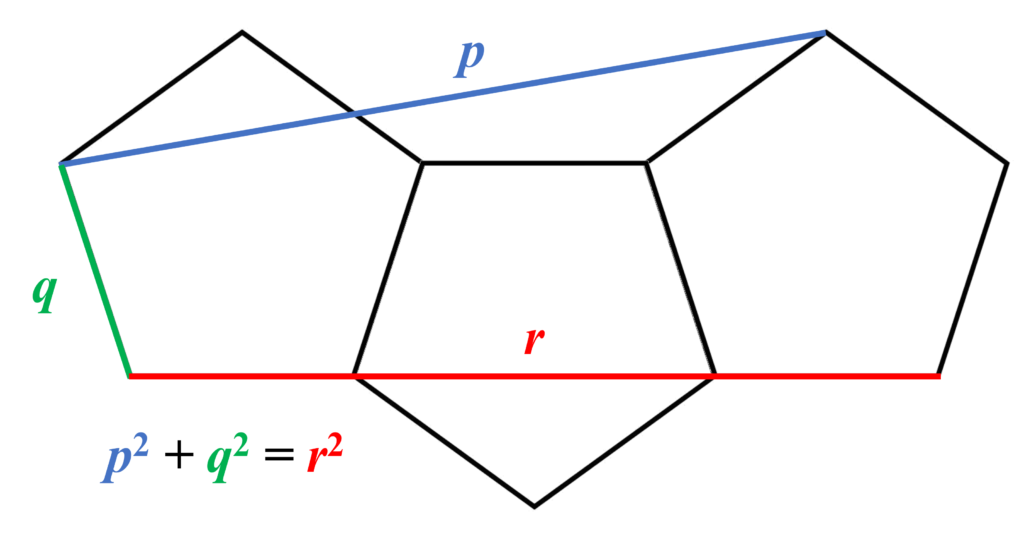
色々な示し方があるでしょうが、余弦定理を使って機械的に示してしまうのが簡明です。正五角形について、一辺の長さを$a$、対角線の長さを$b$とし、図に示した角度を$\theta$と置きます。
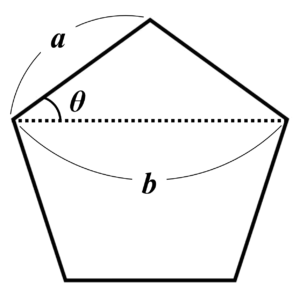
このとき、$q=a$、$r=2a+b$ となります。等辺が$a$、底角が$\theta$、底辺が$b$の二等辺三角形について余弦定理を適用することにより、$$a^2=a^2+b^2-2ab\cos \theta$$ $$\therefore 2a\cos \theta =b \quad \cdots (*)$$を得ます。
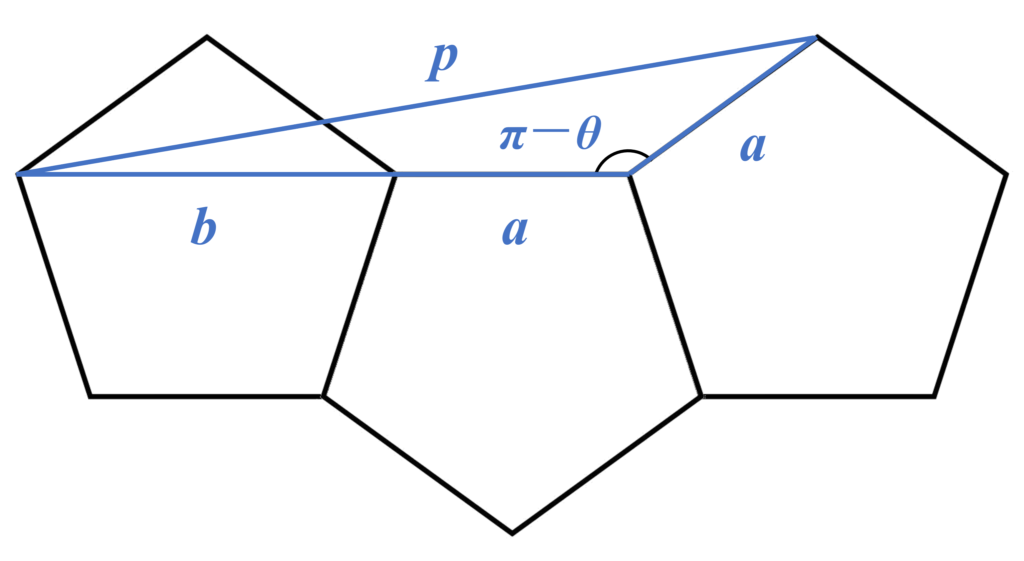
また、上図の青色の三角形について余弦定理を適用することにより、$$\small \begin{align} p^2 &=a^2+(a+b)^2-2a(a+b)\cos (\pi-\theta) \\ &=a^2+(a+b)^2+2a(a+b)\cos \theta \end{align}$$となるので、$(*)$を代入して整理することにより、$$p^2=2a^2+3ab+2b^2$$を得ます。
よって、$$r^2-p^2-q^2=a^2+ab-b^2$$となるので、この右辺が$0$になることを示せばOKです。この証明にも色々なやり方があるでしょうが、ひとつは、正五角形についてトレミーの定理を用いて $\small b=\dfrac{\sqrt{5}+1}{2}a$ を求め、これを代入するという方法で示せます。
以上で $p^2+q^2=r^2$ を示せる訳ですが、何だかエレガントではないような気がします。この関係式は初等的に(三角関数を用いない純粋な幾何的方法で)証明できそうに思われるのですが、未だ上手い方法を思い付けないでいます。複素数を使って示すこともできそうですが、結局は三角関数を用いた偏角の議論が必要になりそうな気がします(気のせい?)。はたまた、実は自明な等式だったりするのでしょうか…?
面白い証明法のアイデアをお持ちの方は是非教えて下さい!(^▽^)/
