数Ⅲ微積で扱われる双曲線関数についてまとめました。本稿では各種双曲線関数の定義とそれらの導関数・不定積分の導出について解説します!
双曲線関数について
双曲線 $H:x^2-y^2=1$ のうち $x>0$ の部分は、実数$t$により$$\small x(t)=\dfrac{e^{t}+e^{-t}}{2},\, y(t)=\dfrac{e^{t}-e^{-t}}{2}$$と媒介変数表示されます。代入してみると分かることですが、これは正しく双曲線 $H$ の点を表しています。
$$\small \lim_{t \to \pm \infty} \dfrac{e^{t}+e^{-t}}{2}=+\infty,\, \lim_{t \to \pm \infty} \dfrac{e^{t}-e^{-t}}{2}=\pm\infty$$であり、相加・相乗平均の不等式より $x(t) \geqq 1$ が成り立つことから、点$\small \left(\dfrac{e^{t}+e^{-t}}{2},\dfrac{e^{t}-e^{-t}}{2}\right)$は双曲線 $H$ の $x>0$ の部分全体を隈なく動くことが分かります。
このように双曲線のパラメータ表示に用いられることから、関数 $\small \dfrac{e^{t}+e^{-t}}{2}$ や $\small \dfrac{e^{t}+e^{-t}}{2}$ は「双曲線関数」と呼ばれています。
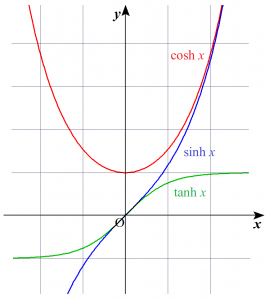
双曲線関数には以下のような種類が存在します。
双曲線関数の一覧
(1)$\sinh x=\dfrac{e^{x}-e^{-x}}{2}$
(2)$\cosh x=\dfrac{e^{x}+e^{-x}}{2}$
(3)$\tanh x=\dfrac{\sinh x}{\cosh x}=\dfrac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$
(4)$\operatorname{cosech} x=\dfrac{1}{\sinh x}$
(5)$\operatorname{sech} x=\dfrac{1}{\cosh x}$
(6)$\operatorname{coth} x=\dfrac{\cosh x}{\sinh x}=\dfrac{e^{x}+e^{-x}}{e^{x}-e^{-x}}$
読み方が少し特殊で、$\sinh$ は「ハイパボリックサイン」とか「ハイパーサイン」、「シャイン」などと呼ばれます。
$\cosh$ は「ハイパボリックコサイン」とか「ハイパーコサイン」、「コッシュ」などと読まれ、$\tanh$ は「ハイパボリックタンジェント」とか「タンエイチ」などと読まれます。
公式 $\small \cosh ^{2} x-\sinh ^{2} x=1$
ここで、$$\small \cosh ^{2} x-\sinh ^{2} x=1$$という重要な公式を紹介しておきます。
これは以下のように証明することができます。$$\small \begin{align}
& \quad \cosh ^{2} x-\sinh ^{2} x \\ &=\left(\frac{e^{x}+e^{-x}}{2}\right)^{2}-\left(\frac{e^{x}-e^{-x}}{2}\right)^{2} \\ &=\frac{e^{2 x}+2+e^{-2 x}}{4}-\frac{e^{2 x}-2+e^{-2 x}}{4} \\ &=1
\end{align}$$この関係式は導関数の導出において利用します。
各種導関数の導出
それでは、各種双曲線関数の導関数を導出していきましょう!
$(\sinh x)^{\prime}=\cosh x$
証明
$$\small \begin{align}
(\sinh x)^{\prime} &=\left(\dfrac{e^{x}-e^{-x}}{2}\right)^{\prime} \\ &=\dfrac{e^{x}+e^{-x}}{2} \\ &=\cosh x
\end{align}$$
$(\cosh x)^{\prime}=\sinh x$
証明
$$\small \begin{align}
(\cosh x)^{\prime} &=\left(\frac{e^{x}+e^{-x}}{2}\right)^{\prime} \\ &=\frac{e^{x}-e^{-x}}{2} \\ &=\sinh x
\end{align}$$
$(\tanh x)^{\prime}=\operatorname{sech}^{2} x$
証明
$$\small \begin{align}
(\tanh x)^{\prime} &=\left(\frac{\sinh x}{\cosh x}\right)^{\prime} \\ &=\frac{(\sinh x)^{\prime} \cosh x-\sinh x(\cosh x)^{\prime}}{(\cosh x)^{2}} \\ &=\frac{(\cosh x)^{2}-(\sinh x)^{2}}{(\cosh x)^{2}} \\ &=\frac{1}{(\cosh x)^{2}} \\ &=\operatorname{sech}^{2} x
\end{align}$$
※途中で $\small \cosh ^{2} x-\sinh ^{2} x=1$ の関係式を使っています。
$(\operatorname{cosech} x)^{\prime}=-\operatorname{coth} x \cdot \operatorname{cosech} x$
証明
$$\small \begin{align}
(\operatorname{cosech} x)^{\prime}&=\left(\frac{1}{\sinh x}\right)^{2} \\ &=-\frac{\cosh x}{(\sinh x)^{2}} \\ &=-\operatorname{coth} x \cdot \operatorname{cosech} x
\end{align}$$
$(\operatorname{sech} x)^{\prime}=-\tanh x \cdot \operatorname{sech} x$
証明
$$\small \begin{align}
(\operatorname{sech} x)^{\prime} &=\left(\frac{1}{\cosh x}\right)^{2} \\ &=-\frac{\sinh x}{(\cosh x)^{2}} \\ &=-\tanh x \cdot \operatorname{sech} x
\end{align}$$
$(\operatorname{coth} x)^{\prime}=-\operatorname{cosech}^{2} x$
証明
$$\small \begin{align}
(\operatorname{coth} x)^{\prime} &=\left(\frac{\cosh x}{\sinh x}\right)^{\prime} \\ &=-\frac{(\cosh x)^{\prime} \sinh x-\cosh x(\sinh x)^{\prime}}{(\sinh x)^{2}} \\ &=\frac{(\sinh x)^{2}-(\cosh x)^{2}}{(\sinh x)^{2}} \\ &=-\frac{1}{(\sinh x)^{2}} \\ &=-\operatorname{cosech}^{2} x
\end{align}$$
※途中で $\small \cosh ^{2} x-\sinh ^{2} x=1$ の関係式を使っています。
各種不定積分の導出
$\sinh x$ や $\cosh x$ の積分は、指数関数の単純な積分になるので全く難しくありません。結果だけ示すと、$$\displaystyle \int \sinh ax\,dx={\frac {1}{a}}\cosh ax+C$$ $$\displaystyle \int \cosh ax\,dx={\frac {1}{a}}\sinh ax+C$$のようになります。
$\tanh x$ の場合は少し難しいかもしれません。$$\int \tanh ax \,dx=\int \frac{e^{ax}-e^{-ax}}{e^{ax}+e^{-ax}} dx$$より、$u=e^{ax}+e^{-ax}$ と置くと、$d u=a(e^{x}-e^{-x})d x$ となるので$$\small \begin{align}
\displaystyle \int \tanh ax \,dx &=\displaystyle \int \frac{e^{ax}-e^{-ax}}{e^{ax}+e^{-ax}} dx \\ &=\displaystyle \frac{1}{a}\int \frac{d u}{u} \\ &=\frac{1}{a}\ln |u|+c \\ &=\frac{1}{a}\ln \left(e^{ax}+e^{-ax}\right)+c \\ &=\frac{1}{a}\ln (2 \cosh (ax))+c \\ &=\frac{1}{a}\ln (\cosh (ax))+(\frac{1}{a}\ln2+c) \\ &=\frac{1}{a}\ln (\cosh (ax))+C
\end{align}$$と求められます。
その他の双曲線関数についても、結果だけ載せておきます。関数の定義に立ち返れば証明は難しくないはずです。$$\int \coth x\,dx=\ln |\sinh x|+C$$ $$\displaystyle \int \operatorname {sech} \,x\,dx=\arctan \,(\sinh x)+C$$ $$\displaystyle \int \operatorname {csch} \,x\,dx=\ln \left|\tanh {x \over 2}\right|+C$$

“【数Ⅲ】双曲線関数の性質まとめ” への1件の返信