数Ⅲ微積の基本事項である自然対数の底eに関連する極限公式についてまとめました。本稿では自然対数の底eの定義と極限公式の導出について解説します。
自然対数の底 $e$ について
自然対数の底 $e$（ネイピア数）がどのように決まる値なのかについて簡単に説明します。
定義に従って指数関数 $f(x)=a^{x}$ の導関数を求めると、$$\begin{align}
f^{\prime}(x) &=\lim _{\varDelta x \to 0} \frac{a^{x+\varDelta x}-a^{x}}{\varDelta x} \\ &=\lim _{\varDelta x \to 0} a^{x} \frac{a^{\varDelta x}-1}{\varDelta x} \\ &=a^{x} \lim _{\varDelta x \to 0} \frac{a^{0+\varDelta x}-a^{0}}{\varDelta x} \\ &=a^{x} f^{\prime}(0) \quad \cdots \color{red}{(*)}
\end{align}$$となります。$f^{\prime}(0)$は関数 $f(x)=a^{x}$ のグラフ上の点$(0,1)$における接線の傾きであり、下の図からも分かる通り$a$の値によって様々に変化します。
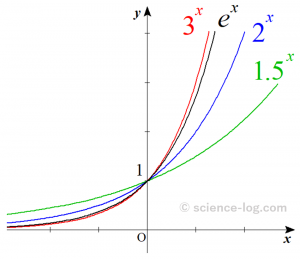図．色々な底の指数関数
色々な$a$の値のうち、接線の傾きが$1$に等しくなるもの、つまりちょうど $f^{\prime}(0)=1$ を満たすものが存在します。これを$e$と置けば$\color{red}{(*)}$より、$$\left\{e^{x}\right\}^{\prime}=e^{x}$$という非常に便利な関係が成り立ちます。
このような実数$e$を底とする対数 $y=\log_e x$ を自然対数と呼び、実数 $e$ を自然対数の底と呼びます。
数学の分野ではあまり見かけませんが、物理学などでは自然対数（natural logarithm）を $\ln x$ と表し、常用対数（底を$10$とする対数）を単に $\log x$ と表すこともあるので注意しましょう。
$\small \displaystyle \lim _{x \to 0}(1+x)^{\frac{1}{x}}=e$ の導出
この関係式は自然対数の底$e$が関係する極限計算において非常に重要で、これを使わないと問題が解けません。ただし、これが成り立つことの証明は高校数学の範囲を超えるため、高校の段階では取り敢えずこういうものなのだと認識しておくに留めるのが普通です。
以下では興味のある方のために、指数関数の連続性を前提としてこの極限公式を導出してみます。
極限公式の導出
$a=e$ のとき $f^{\prime}(0)=1$ となるので、微分係数の定義より$$\lim _{\varDelta x \to 0} \dfrac{e^{0+\varDelta x}-e^{0}}{\varDelta x}=1$$が成り立ちます。ここで $\varDelta x$ を $h$ と置き直すと、$$\displaystyle \lim _{h \to 0} \dfrac{e^{h}-1}{h}=1$$という皆さんがよく知っている関係式に書き直せます。
ここで $e^{h}-1=k$ と置くと、$h=\log (1+k)$ となり $h \to 0$ のとき $k \to 0$ となります。この置き換えにより、$$\displaystyle \lim _{k \to 0} \dfrac{k}{\log (1+k)}=1$$となり、逆数をとって$$\displaystyle \lim _{k \to 0} \dfrac{\log (1+k)}{k}=1$$つまり$$\displaystyle \lim _{k \to 0} \log (1+k)^{\frac{1}{k}}=1$$となります。
ここで、対数関数は連続関数であること、および、対数の底が$e$であることに注意すると、$$\begin{align} \displaystyle & \lim _{k \to 0} \log (1+k)^{\frac{1}{k}}=1 \\ \therefore \quad \displaystyle & \log \left(\lim _{k \to 0}(1+k)^{\frac{1}{k}}\right)=1 \\ \therefore \quad \displaystyle & \lim _{k \to 0}(1+k)^{\frac{1}{k}}=e \end{align}$$を得ます。
これより $k=x$ とすればそのまま$$\displaystyle \lim _{x \to 0}(1+x)^{\frac{1}{x}}=e$$が得られ、$k=\dfrac{1}{x}$ とすれば、$k \to \pm 0$ のとき $x \to \pm \infty$ となるので、$$\lim _{x \to \pm \infty}\left(1+\frac{1}{x}\right)^{x}=e$$が得られます。
この関係式を使って色々な極限値を求めることができます。以下の例題で公式の使い方を確認しましょう。
例題
実際に手を動かしてみることをお勧めします！
（１）$\displaystyle \lim _{x \to 0} (1-n x)^{\frac{1}{x}}$（$n$は整数）
» （１）の解答例
$$\begin{aligned}
\lim _{x \to 0}(1-n x)^{\frac{1}{x}} &=\lim _{x \to 0}\left\{(1-n x)^{\frac{1}{-n x}}\right\}^{-n} \\ &=e^{-n} \\ &=\color{red}{\frac{1}{e^{n}}}
\end{aligned}$$※ $n$は整数としていますが、この結果は任意の実数で成り立ちます。
» 閉じる
（２）$\displaystyle \lim _{x \to \infty}\left(\frac{x-1}{x+1}\right)^{x}$
» （２）の解答例
$$\frac{x-1}{x+1}=1-\frac{2}{x+1}$$と変形できるから、$t=-\dfrac{2}{x+1}$ と置くと、$x=-\dfrac{2+t}{t}$ となり、$x \to \infty$ のとき $t \to 0$ となる。よって、$$\begin{aligned}
\lim _{x \to \infty}\left(\frac{x-1}{x+1}\right)^{x} &=\lim _{x \to \infty}\left(1-\frac{2}{x+1}\right)^{x} \\ &=\lim _{t \to 0}(1+t)^{-\frac{t+2}{t}} \\ &=\lim _{t \to 0}\left\{(1+t)^{\frac{1}{t}}\right\}^{(-t-2)} \\
&=e^{(0-2)} \\ &=e^{-2} \\ &=\color{red}{\frac{1}{e^{2}}}
\end{aligned}$$を得る。
» 閉じる
（３）$\displaystyle \lim _{x \to \infty}\left(1-\dfrac{3}{x}-\dfrac{4}{x^2}\right)^{x}$
» （３）の解答例
$$\left(1-\dfrac{3}{x}-\dfrac{4}{x^2}\right)^{x}=\left(1-\dfrac{4}{x}\right)^{x}\left(1+\dfrac{1}{x}\right)^{x}$$より、
$$\begin{aligned}
& \quad \lim _{x \to \infty}\left(1-\dfrac{3}{x}-\dfrac{4}{x^2}\right)^{x} \\ &=\lim _{x \to \infty}\left(1-\dfrac{4}{x}\right)^{x}\left(1+\dfrac{1}{x}\right)^{x} \\ &=\lim _{x \to \infty}\left\{\left(1-\dfrac{4}{x}\right)^{-\frac{x}{4}}\right\}^{-4}\left(1+\dfrac{1}{x}\right)^{x} \\
&=e^{-4} \cdot e \\ &=e^{-3} \\ &=\color{red}{\frac{1}{e^{3}}}
\end{aligned}$$を得る。
» 閉じる