「無限」という概念は、直感が通用しない不思議な世界を生み出すことがあります。今回はこうした「極限」や「無限」の世界を色々な例で覗いてみましょう。
$1/3=0.3333…$の例
人生で最初に出会う無限の概念は恐らく小数の表記でしょう。$$\dfrac{1}{3}=0.3333…$$という関係式一つを例にとっても、無限という概念の掴み所の無さが見えてきます。
$1$を$3$で割った値を分数で表せば$$\dfrac{1}{3}$$とすっきりした形で表現できますが、これを小数表示すると$$0.3333…$$となります。もはや見慣れている感がありますが、これは一見すると奇妙な表現です。「$3$」は一体どこまで続いているのでしょうか?どこかで終わるのではないでしょうか?
例えば小学生に$$\dfrac{1}{3}=0.3333…$$という関係を教える場合を考えてみましょう。筆算、もしくは電卓を使い、取り敢えず「$1 \div 3$」の値が「$0.3333…$」という小数点以下に$3$がずっと続く数になりそうだということを理解してもらいます。そして黒板にこの式を書き、さらに両辺に$3$を掛けて、
「$3$を掛けて元に戻すと$1$になりますね!」
なんて言ってみせても良いのですが、洞察力の鋭い小学生なら、
「え~?$1$と$0.9999\cdots$の間には絶対スキマがあるよ!」
と言って先生を困らせることでしょう。$0.3333…$が$\dfrac{1}{3}$に一致することは(殊更、小学生にとっては)自明なことではありません(※最近の電卓なら $1 \div 3$ という処理を記憶しておくため、親切に $0.3333… \times 3=1$ と返してくれます)。
少し学年が上がった中学生にこれを教えるときは文字を使って誤魔化すこともできそうです。
証明?
$a=0.3333…$ と置くと、$\dfrac{1}{10}a=0.0333\cdots$ となる。
したがって、$$a-\dfrac{1}{10}a=(0.3333…)-(0.0333…)$$ $$\therefore \dfrac{9}{10}a=0.3\ \left(=\dfrac{3}{10}\right)$$ $$\therefore a=\dfrac{1}{3}$$と求められる。
□
しかし残念ながらこれも根本的な解決になっていません。上記の例では $a=0.3333…$ より、$$3a=0.9999…$$となりますが、$a=\dfrac{1}{3}$ より、この左辺は$1$に等しくなりますから、$$1=0.9999…$$が成り立ちます。結局この証明も、とても小さいように思われるけれども視覚的には確実に存在する$1$と$0.9999…$の「スキマ」については何の説明も果たしていません。それに、$0.3333…$と$0.0333…$の「$…$」の部分は本当に同じと言えるのでしょうか?
高校数学で「極限」の内容を学ぶと、何となくこの辺りの事情が分かった気になれます。数列$\{a_n\}$を $a_n=1-\dfrac{1}{10^n}$ と定義すると$$0.9999\cdots=\lim_{n \to \infty}a_n$$と言えそうです。$n$が無限大の大きさになれば$\dfrac{1}{10^n}$はほとんどゼロなので、数列$\{a_n\}$は$1$に収束することが数式によって理解できます。ただし「一致する」とは一言も述べられず「限りなく近付く」という表現しか用いられないので、高校数学の時点でも何だか釈然とせずに通過するだけで終わってしまいます。大学で$\varepsilon$-$\delta$論法を学ぶことで、やっと「実数の
大学数学で学ぶ「単調増加で、かつ上に有界な数列は上限値に収束する」という定理によって、$$1=0.9999…$$という表記を数学的な根拠をもって許容するに至る訳ですが、この小学生でも気が付くような疑問に大学数学を動員しなければならないというのは何となく腑に落ちないように思えますね。
これは円周率$\pi$が小数点以下無限桁まで続いていくのと本質的には同じことです($\dfrac{1}{3}$は有理数で$\pi$は無理数という違いはありますが)。$3$進法を使えば$\dfrac{1}{3}$は「$0.1$」と表すことができますが、例えば$\dfrac{1}{2}$は$3$進法だと$$\dfrac{1}{2}=0.1111…_{(3)}$$となり、小数点以下に$1$が無限に続く循環小数となります。これは$3$が$2$で割り切れないために起きる現象であり、同様に$10$が$3$で割り切れないために十進法では$\dfrac{1}{3}$は小数点以下に$3$が無限に続く循環小数としてしか表すことができません。
ですから、何進法を使ったとしても、こうした小数点以下が無限に続く実数が存在するのはどうしようもないことなのです。もちろん、「$\pi$進法」なるものを使えば$3.1415…$という数も「$10_{(\pi)}$」と表記することは一応可能です・・・が、無理数進法の考察は不毛玄人向けです(笑)。
級数「$1/2^n$の無限和」を図形で見る
$1$の半分は$\dfrac{1}{2}$です。その半分は$\dfrac{1}{4}$で、さらに半分は$\dfrac{1}{8}$・・・となりますが、これらの和は幾つになるのでしょうか?
等比数列の和の公式により、初項を$a$、公比を$x$とすると$$\sum^{n}_{k=1}ax^{k-1}=\dfrac{a(1-x^{n})}{1-x}$$となるので、$|x|<1$ のとき $\displaystyle \lim_{n \to \infty}x^{n}=0$ より、等比級数の部分和は$$\dfrac{a}{1-x}$$に収束します。
$$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\cdots+\dfrac{1}{2^n}+\cdots$$という級数を考えてみます。先程の公式に当てはめると、$a=\dfrac{1}{2}$、$x=\dfrac{1}{2}$ ですから、この値は$1$に収束することが分かります。
公式を使う方法は高校生でないと使えませんが、実はこの級数は小学生でも理解できる方法があります。一辺が$1$の長さを持つ正方形を次々に半分に分割していくと、ちょうど元の正方形に重なります。これがこの級数の正体です。
 図1.正方形の分割
図1.正方形の分割
どうでしょうか?分割された四角形の面積はそれぞれ$2$の冪の逆数となっており、全体の和が$1$になりそうだということが直感的に理解できると思います。ここでは分かりやすくgif画像にしていますが、黒板やホワイトボードで実演しても良いですし、実際に生徒に描いてもらっても良いかもしれません。
有理数?それとも無理数?
$\dfrac{1}{2}$は最も簡単な有理数であり、$\sqrt{2}$は最も簡単な無理数です。しかしこれに「無限」が関与すると様子が変わります。
例えば、$$\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{\ddots}}}}}$$という数は幾つになるでしょうか?
ちょっと計算してみましょう。
$$\dfrac{1}{1+\dfrac{1}{1}}=\dfrac{1}{2}$$
$$\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1}}}=\dfrac{2}{3}$$
$$\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1}}}}=\dfrac{3}{5}$$
$$\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1}}}}}=\dfrac{5}{8}$$
$$\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1}}}}}}=\dfrac{8}{13}$$勘が良い人なら分かってしまうかもしれませんが、分子、分母に出現する数字はすべてフィボナッチ数であることが帰納的に証明できそうです。実際その通りで、$$\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{\ddots}}}}}$$は隣り合うフィボナッチ数の比の極限値である$$\dfrac{\sqrt{5}-1}{2}$$に一致します。
» 証明はこちら
(証明)$$\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{\ddots}}}=x$$と置くと、分数は入れ子になっているので$$\cfrac{1}{1+x}=x$$となる。これより、$$x^2+x-1=0$$を得るが、$x$は負ではないので$$x=\dfrac{\sqrt{5}-1}{2}$$となる。
» 閉じる
これは見た目からは全く想像できない結果です。分数からは極限値も有理数になると考えるのが自然ですが、実際には得体の知れない(?)$\dfrac{\sqrt{5}-1}{2}$という値に収束します。これはいわゆる「黄金比」と呼ばれる数で、美しいものに必ず現れるという都市伝説学説があり、かの有名な「ミロのヴィーナス」や、ギリシャの首都アテネにある「パルテノン神殿」にも登場します。
 図2.ミロのヴィーナス
図2.ミロのヴィーナス
 図3.パルテノン神殿
図3.パルテノン神殿
● ● ●
$\sqrt{2}$を無限に入れ子にしても面白い結果が得られます。$$\sqrt{2}=1.414213…$$
$$\sqrt{2+\sqrt{2}}=1.847759…$$
$$\sqrt{2+\sqrt{2+\sqrt{2}}}=1.961570…$$
$$\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}=1.990369…$$
$$\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}=1.997590…$$見ての通り、こちらの入れ子の平方根は$2$に近付いていきます。実際、$$\sqrt{2+\sqrt{2+\sqrt{2+\cdots}}}=2$$となることが証明可能です。
» 証明はこちら
(証明)$$\sqrt{2+\sqrt{2+\sqrt{2+\cdots}}}=x$$と置くと、根号の中は入れ子になっているので$$\sqrt{2+x}=x$$となる。これより、$$x^2-x-2=0$$ $$\therefore (x-2)(x+1)=0$$を得るが、$x$は負ではないので$$x=2$$となる。
» 閉じる
一見すると無理数に見えるのに、「無限」が絡むと有理数に変身してしまうなんて不思議な話ですね。
ここで少し一般化してみます。$a$を負でない実数として$$\sqrt{a+\sqrt{a+\sqrt{a+\cdots}}}=x$$と置くと、根号の中は入れ子になっているので$$\sqrt{a+x}=x$$となります。これより、$$x^2-x-a=0$$となるので、二次方程式の解の公式から $x=\dfrac{1 \pm \sqrt{1+4a}}{2}$ と求められます。いま$x$は負ではないので、$$x=\dfrac{1+ \sqrt{1+4a}}{2}$$に決まります。
$a=2$ とすると先程の結果が得られます。また、$a=1$ とすれば「黄金比」が登場します。
※$\dfrac{\sqrt{5}-1}{2}$と$\dfrac{\sqrt{5}+1}{2}$は親戚みたいな関係で、どちらも「黄金比」と呼ばれることがあります。
さて、ここで $a=0$ を入れてみると、$x=1$ となります。ところが、これを元々の式に代入すると$$\sqrt{0+\sqrt{0+\sqrt{0+\cdots}}}=1$$となります!左辺には$0$しかなく、右辺はどう見ても$1$です。これより $0=1$ が成り立つので、両辺に$1$を加えると何と$$1=2$$が成立してしまいます!
・・・もちろんジョークなのですが、どこがどうおかしいのかを考えているとよく分からなくなってきませんか(笑)?
※因みに、この証明は2019年7月27日現在、「$1=2$」の証明法が最も充実(?)している日本語版アンサイクロペディアでも紹介されていないようです。(2021/09/29追記:今なお紹介されていませんでした)
無限に続くフラクタル図形
皆さんは「ロマネスコ」という野菜をご存知でしょうか?
 図4.ロマネスコ
図4.ロマネスコ
独特のフラクタル形(自己相似形)のつぼみが特徴的な野菜で、つぼみや突起の数はフィボナッチ数と関係しています。つぼみには螺旋状に突起が付いており、さらにこの突起に螺旋状に突起が生えています。このように倍率を上げても元と同じような相似形の形状が現れる図形を「フラクタル図形」と言います。
※ロマネスコに関しては勘違いされている人も散見されるので断っておきますが、螺旋状の図形は別にフラクタルとは言いません。拡大して見たときに元と同じ図形が見えてくることをフラクタルと言います。
さて、最も有名なフラクタル図形と言えばコッホ曲線です。以下の図形は「コッホ雪片」として知られている図形です。
 図5.コッホ雪片の生成過程
図5.コッホ雪片の生成過程
このように自己相似形の構造をもつ図形を「フラクタル図形」と呼びます。ここでも無限の概念が登場します。
 図6.コッホ曲線を拡大する動画
図6.コッホ曲線を拡大する動画
どんなに拡大しても無限に同じ図形が出てきます。これがフラクタルという性質です。最終的に生成するコッホ雪片(図7)の面積は元の正三角形の面積の$\dfrac{8}{5}$となりますが、辺の長さは無限大に発散することが知られています。
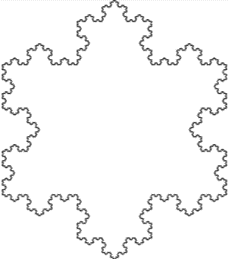 図7.コッホ雪片
図7.コッホ雪片
あまり詳しくは紹介しませんが、フラクタル幾何学において、「$1/k$ 倍に縮めると、もとの図形を作るには $N = k^D$ 個の図形が必要となる」という意味で「フラクタル次元$D$」というものが定義されています。
これは例えば、長さ1の線分を$1/3$ 倍に縮めると、もとの図形を作るには $N = 3^{\color{red}{1}}$ 個の図形が必要となります。したがってこの線分のフラクタル次元は$\color{red}{1}$です(これは直線が1次元、ということに相当しています)。
この定義に基づけば、コッホ曲線を$1/3$ 倍に縮めると、もとの図形を作るには $4$ 個の図形が必要となります。したがってコッホ曲線のフラクタル次元は$$\dfrac{\log 4}{\log 3} \approx 1.262$$となります。因みにほとんどのフラクタル図形の次元は非整数になることが知られています。また、これより、コッホ曲線のフラクタル次元は$1$より大きいので、境界線の総延長が無限大に発散することが分かります。
他にもシェルピンスキーの三角形やドラゴン曲線など、様々なフラクタル図形が知られています。
 図8.シェルピンスキーの三角形
図8.シェルピンスキーの三角形
 図9.ドラゴン曲線
図9.ドラゴン曲線
中でも有名なのがマンデルブロ集合でしょう。これは
「漸化式$$\begin{cases}z_{{n+1}}=z_{n}^{2}+c\\z_{0}=0\end{cases}$$で定義される複素数列 ${z_n};\ n \in N \cup 0$ が $n \to \infty$ としたときに無限大に発散しない」
という条件を満たす複素数 $c$ 全体からなる集合として定義されます。
 図10.マンデルブロ集合
図10.マンデルブロ集合
3次元のフラクタル図形も知られています。初めに紹介したロマネスコも3次元のフラクタル図形と言えるでしょう。以下はフラクタルな立体図形として有名なメンガーのスポンジです。
 図11.メンガーのスポンジ
図11.メンガーのスポンジ
メンガーのスポンジは立方体に規則的に穴を空けて生成される図形で、フラクタル次元は $\dfrac {\log 20}{\log 3} \approx 2.729$ 次元となります。フラクタル次元が$2$より大きく$3$より小さいので、表面積は無限大に発散し、体積は$0$に収束します。体積は$0$なのに表面積は無限というのは何とも不思議な図形ですね!
無限の世界がいかに奇妙か何となくお分かり頂けたのではないでしょうか。とはいえ、これらは無限の世界のごく一部に過ぎません。皆さんも無限に関するお気に入りの定理や現象を見つけてみて下さい!
(2021/09/29追記:記事中のスタイルを一部変更)

“ちょっと面白い「無限」の話” への1件の返信