オイラーの素数生成式に関する雑談記事です。
$$f(n)=n^{2}-n+41$$という式は $1 \leqq n \leqq 40$ の範囲で異なる40個の素数の値を与えることが知られています。これは「オイラーの素数生成(多項)式」と呼ばれる有名な二次式です。
この多項式によって得られる最初の40個の素数を列挙してみます。
| $n$ | $f(n)$ |
| 1 | 41 |
| 2 | 43 |
| 3 | 47 |
| 4 | 53 |
| 5 | 61 |
| 6 | 71 |
| 7 | 83 |
| 8 | 97 |
| 9 | 113 |
| 10 | 131 |
| 11 | 151 |
| 12 | 173 |
| 13 | 197 |
| 14 | 223 |
| 15 | 251 |
| 16 | 281 |
| 17 | 313 |
| 18 | 347 |
| 19 | 383 |
| 20 | 421 |
| 21 | 461 |
| 22 | 503 |
| 23 | 547 |
| 24 | 593 |
| 25 | 641 |
| 26 | 691 |
| 27 | 743 |
| 28 | 797 |
| 29 | 853 |
| 30 | 911 |
| 31 | 971 |
| 32 | 1033 |
| 33 | 1097 |
| 34 | 1163 |
| 35 | 1231 |
| 36 | 1301 |
| 37 | 1373 |
| 38 | 1447 |
| 39 | 1523 |
| 40 | 1601 |
このようにオイラーの素数生成式は連続して$40$個もの素数を与えます。$n=41$ のときは $f(41)=41^2$ となって初めて素数でなくなります。
なお、この二次式はゼロ以下の場合でも素数値を与えますが $f(n)=f(-n+1)$ なので$n$が正のときを考えれば十分です($n^2+n+41$ を考えることに相当するので重複しています)。
$f(n)$は $1 \leqq n \leqq 100$ の範囲ではその半数以上の86個の$n$について素数を与えます。範囲を広げて調べてみると以下の結果を得ます。
| 範囲 | 素数を与える$n$の個数 |
| $1 \leqq n \leqq 10^2$ | 86 |
| $1 \leqq n \leqq 10^3$ | 581 |
| $1 \leqq n \leqq 10^4$ | 4149 |
| $1 \leqq n \leqq 10^5$ | 31985 |
| $1 \leqq n \leqq 10^6$ | 261081 |
| $1 \leqq n \leqq 10^7$ | 2208197 |
| $1 \leqq n \leqq 10^8$ | 19132652 |
この結果から、$1 \leqq n \leqq 10^k$ の範囲で素数を与える$n$の個数を$N(k)$と置くと、$$N(k) \approx e^{2.0918 k} \approx 10^{0.9084 k}$$という関係式が得られます。これは下図に示した$k$と$\log_{10}N(k)$の間に成り立つ直線関係から求めたものです(青色折れ線は$\log_{10}N(k)$のプロット、橙色破線は原点を通る近似直線)。
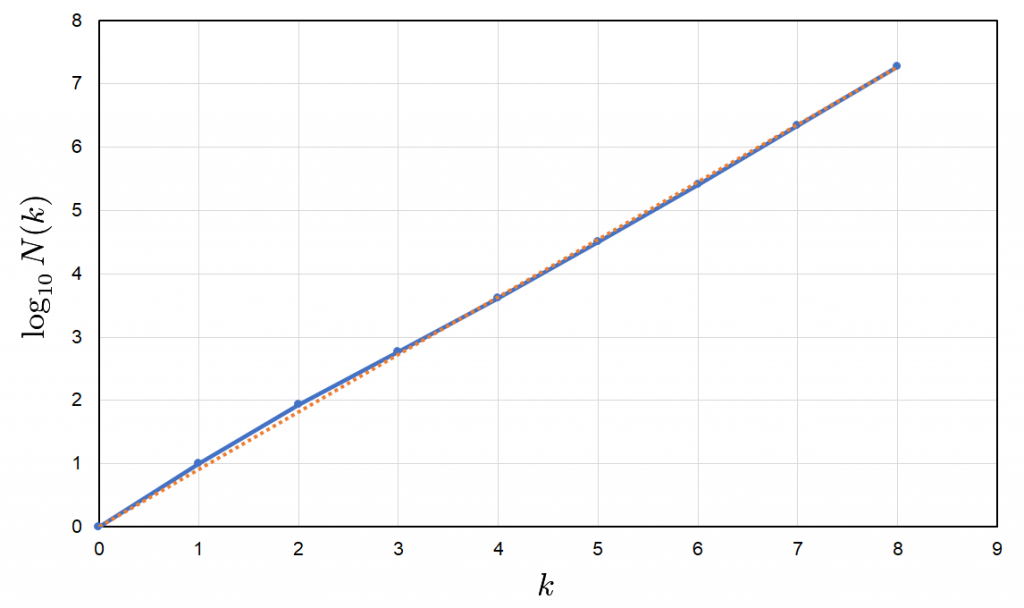 図.$k$と$\log_{10}N(k)$の直線関係
図.$k$と$\log_{10}N(k)$の直線関係
ここまで多くの素数値を与えるのは定数項が$41$の場合に特有の性質と言えます。例えば $n^2-n+15$ の場合、$1 \leqq n \leqq 10^3$ の範囲で素数を与える整数$n$は68個しかありません。
$f_q(n)=n^2-n+q$ と置くとき、$f_{15}(n)$が素数になる$n$の個数を調べると以下のようになり、$f_{41}(n)$に比べて明らかに少ない結果を得ます。
| 範囲 | $f_{15}(n)$が素数になる$n$の個数 |
| $1 \leqq n \leqq 10^2$ | 11 |
| $1 \leqq n \leqq 10^3$ | 68 |
| $1 \leqq n \leqq 10^4$ | 470 |
| $1 \leqq n \leqq 10^5$ | 3634 |
| $1 \leqq n \leqq 10^6$ | 29525 |
| $1 \leqq n \leqq 10^7$ | 249551 |
| $1 \leqq n \leqq 10^8$ | 2162730 |
$q$を素数として$f_{13}(n)$を調べても、$q=41$ の場合ほどは多くありません。
| 範囲 | $f_{13}(n)$が素数になる$n$の個数 |
| $1 \leqq n \leqq 10^2$ | 19 |
| $1 \leqq n \leqq 10^3$ | 126 |
| $1 \leqq n \leqq 10^4$ | 885 |
| $1 \leqq n \leqq 10^5$ | 6850 |
| $1 \leqq n \leqq 10^6$ | 55791 |
| $1 \leqq n \leqq 10^7$ | 472233 |
| $1 \leqq n \leqq 10^8$ | 4092968 |
試しに多項式 $f_q(n)=n^2-n+q$ について $q$ の値を$1$~$1000$までで色々変え、$1 \leqq n \leqq 10^5$ の範囲で素数を与える$n$の個数を調べてみると、上位10位は下の表のようになります。
| $q$ | 素数を与える$n$の個数 |
| 41 | 31985 |
| 941 | 25445 |
| 671 | 25290 |
| 107 | 25162 |
| 227 | 24658 |
| 101 | 24549 |
| 221 | 24305 |
| 881 | 24270 |
| 857 | 23911 |
| 587 | 23786 |
$q=41$ のときに飛び抜けて多いという結果になりました。
多項式$f_q(n)$について、$q$が$2$、$3$、$5$、$11$、$17$、$41$のとき、$1 \leqq n \leqq q-1$ の自然数を代入すると素数になることが知られており、これらの素数をまとめて “Lucky numbers of Euler”「オイラーの幸運数」と呼びます。しかし、$q=41$ の場合について、より大きな$n$についても$f(n)$が多数の素数値を与えることはあまり知られていないように思います。
きいねく氏によれば、ウラムの螺旋に類する$f_q(n)$のプロットを描くと以下のようになるそうです。$q=41$ の場合は特に黒く塗り潰されており、より広範囲の$n$についても素数になっていることが視覚的に理解できます。これはなかなか興味深い性質です。
tsujimotterさんの素数生成多項式が素数を生み出す割合を計算してるのを見て,多項式pに対して,ウラムの螺旋の要領でp(n)が素数となる点を黒く塗りつぶした図を作ってみました.
n^2+n+41 がかなり真っ黒です. pic.twitter.com/Mje8gTNLrc— きいねく (@Keyneqq) February 3, 2021
定数項$q$が特定の数の場合に多項式$f_q(n)$が多数の素数を与える現象は「ヘーグナー(Heegner)数」との関係が深いことが背景にありますが、難解なのでここでは詳しく立ち入りません。興味のある方はtsujimotter氏の「オイラーの素数生成多項式の秘密」のページを参考にして下さい。2次体、類数、ラビノヴィッチの定理などについても併せて調べてみると良いでしょう。
2020年の奈良教育大学の入試に次のような問題が出題されています。
以下の問に答えよ。
(1)$n$を自然数とするとき、$n^3+2n$ は$3$の倍数であることを証明せよ。
(2)次の命題が真または偽であることを示せ。
「$n$を自然数とするとき、$n^{2}-n+41$は素数である。」
2020年奈良教育大学 前期(数学教育専修) 第1問
(2)の式はまさにオイラーの素数生成式そのもので、$n=41$ を代入すれば命題が偽であることが示されます。
昔、慶応大学の数学に多項式$f(n)$がすべての整数$n$について素数なら$f(n)$は定数関数であることを証明させる問題が出題されていたと記憶しています。この事実を何となく知っているだけでも二次式が常に素数になることは無さそうだと判断できます。一方で$n$を自然数として$n^{2}-n+41$という形で表せる素数(オイラー素数)が無数に存在するかどうかは知られていない(恐らく無数に存在するでしょうが証明されていない)ように思います。
また、過去には国際数学オリンピック(IMO)にもオイラーの素数生成式が登場したことがあります。
Let $n\ge2$ be an integer. Prove that if $k^2+k+n$ is prime for all integers $k$ such that $0\le k\le\sqrt{\dfrac n 3}$, then $k^2+k+n$ is prime for all integers $k$ such that $0\le k\le n-2$.
IMO 1987, Day 2, Problem 6(キューバ大会)
本問は「$n$を自然数として $f(k)=k^{2}+k+n$ と置くとき、$f(0), f(1), \cdots, f\left(\left[\sqrt{\dfrac{n}{3}}\,\right]\right)$がすべて素数であれば、$f(0), f(1), \cdots f(n-2)$はすべて素数であることを示せ。」と読み替えられます。
$k^2 + k + n$ が合成数になるような$\left[\sqrt{\dfrac{n}{3}}\,\right]$以上 $n-2$ 以下の整数$k$が存在するとして、$f(k)$を割り切るような最小の素数$p$を仮定して矛盾を導く、という方法で証明されます。
これを定理として使えば、例えば $k^2+k+11$ について、$f(0)$、$f(1)$、$f(2)$、$f(3)$が素数になるので残りの$f(4)$~$f(9)$も素数になることが従います。また、$k^2+k+13$ の場合は $f(1)=15$ となり素数でないので素数生成式に該当しないことが直ちに分かります。
ところで、$$41^2-41+41=41^2$$ $$45^2-45+41=2021=43 \times 47$$ $$50^2-50+41=2491=47 \times 53$$となりますが、これらの素因数はいずれも$f_{41}(n)$の素数値として得られるものであり、ここから何らかの規則性が見出せそうにも思われます。
しかし、$$f_{41}(82)=6683=41 \times 163$$となり$f_{41}(n)$の値として登場しない素因数$163$が現れるので、これは単なる思い違いのようです。
そもそも$$f_{41}(n)=n^{2}-n+41$$から得られる整数を素因数分解したときに$\underline{41}$未満の素因数が現れることはないので、小さめの$n$に対して$f_{41}(n)$が与える素数値と$f_{41}(n)$の素因数分解に現れる素数が少し似ているように見える、というだけのことです。
なお、下線部の事実は各素数を法とする剰余類を調べることで示されます。素数$p$について$$f(n+p) \equiv f(n) \pmod{p}$$となるので $1 \leqq n \leqq p$ の範囲で調べれば十分です。いま、$1 \leqq n \leqq 40$ の範囲のすべての整数$n$に対して$f_{41}(n)$は$41$以上の素数となるので、$f_{41}(n)$が$40$以下の素数$p$で割り切れることはありません。したがって、任意の整数$n$に対して$f_{41}(n)$は$41$未満の素因数を含むことはありません。当然ですが、素数だけでなく$2$~$40$までの整数についても同様に$f_{41}(n)$を割り切らないことが言えます。
(参考:素数一覧表)

「f[41](n)=n^2-n+41の値に41未満の素因数が現れることはない」
ことを示すには,
「各素数を法とする剰余類を調べる」わけですが,
その手続きは,(個別に1つずつ行うとすればかなり大変ですが,そうでなければ)
さほど煩雑な計算はしないで完結しますし,
明記しておく方がよさそうな気がします.
言わずもがなですが,以下のようになりますね.
[1]
f[41](n) (n=0,1,2,…,40)はすべて素数であり,41未満のものはないので,
どれも,41未満の素数pで割った余りは0ではない.
[2]
f[41](n+p)とf[41](n)は,pで割った余りは等しい.
よって,nをpで割った余りが定まれば,f[41](n)をpで割った余りは定まる.
[3]
p<41だから,任意の自然数は,
0,1,2,…,40の少なくとも1つとpで割った余りが等しい.
以上[1],[2],[3]より,f[41](n)は,41未満の素数pで割り切れることはない.
たけちゃん さん
コメントありがとうございます。
仰る通り、各素数について個別に論じる必要はありませんね。
簡単にですが加筆しました。ご指摘ありがとうございます。